Основные конструкции фильтров расчет фильтров: , , :: :: | ecolowind.ru
Содержание
Расчет фильтров
Одной из основных задач при расчете фильтров, предназначенных для очистки жидкостей, является определение конструктивных и эксплуатационных параметров фильтрующего элемента или фильтрующего пакета, если последний состоит из нескольких элементов. К числу этих параметров относятся площадь фильтрующей перегородки, гидравлическое сопротивление и ресурс работы фильтра. Исходные данные для выбора указанных параметров, а также основной показатель, характеризующий работу фильтра — тонкость фильтрования — определяют, исходя из двух основных условий: вид очищаемой жидкости и место установки фильтра.[ …]
Физико-химические свойства жидкости (вязкость, плотность, химическая активность, температура кипения и т. п.) оказывают существенное влияние как на процесс фильтрования, так и на конструкцию фильтрующего элемента. Место установки фильтра определяет условия его эксплуатации и вытекающие отсюда: тонкость очистки жидкости, необходимая пропускная способность фильтрующего элемента или пакета, габаритные размеры и масса фильтра, а также дополнительные требования — виброустойчивость, работоспособность при низких или высоких температурах, стойкость к другим внешним воздействиям и т. п.[ …]
п.[ …]
Максимально допустимый перепад давлений при фильтровании жидкости с постоянной скоростью через фильтрующий материал определяют из соображений обеспечения необходимых фильтрационных показателей этого процесса, так как эффективность очистки жидкости может существенно уменьшаться при возрастании перепада давлений [59].[ …]
Полученную по формуле (У.б) площадь фильтрующей перегородки проверяют с тем, чтобы установить, соответствует ли грязеемкость фильтра заданному ре-сурсу работы. Если это условие при найденной площади фильтрующего материала не соблюдается, то эту площадь соответственно увеличивают. Затем выбирают наиболее рациональную форму площади фильтрующей перегородки, исходя из требований к габаритным размерам проектируемого фильтра, а также из свойств фильтрующего материала. Если не представляется возможным обеспечить необходимую площадь при гладкой поверхности фильтрующего элемента, то применяют конструкции из числа описанных в гл. IV. При этом нужно стремиться к максимальному использованию объема, занимаемого фильтрующим элементом, однако следует учитывать также сложность изготовления элемента той или иной конструкции.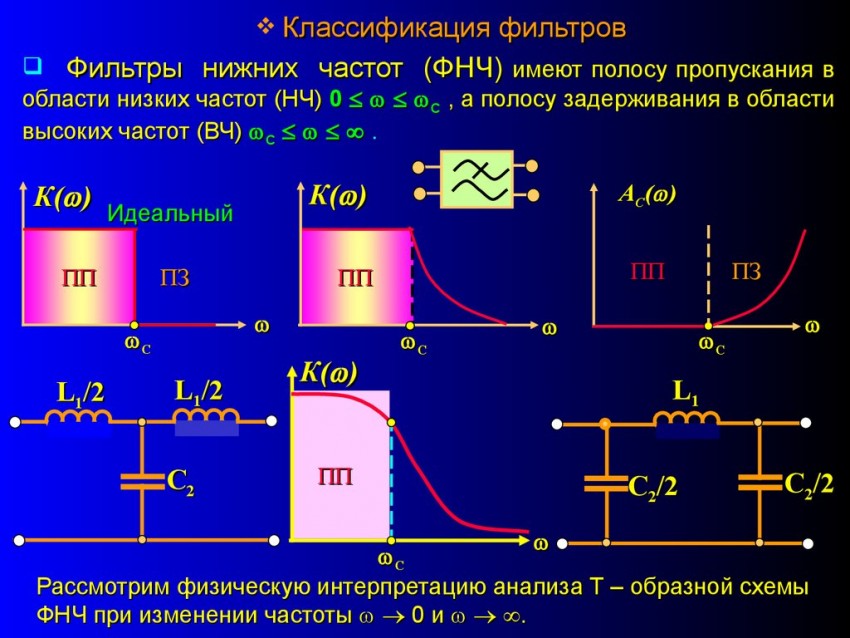 Рабочая поверхность фильтрующих элементов различной конфигурации в зависимости от их габаритных размеров может быть вычислена по формулам, приведенным в табл. 35. Вывод этих формул дается в работе [7].[ …]
Рабочая поверхность фильтрующих элементов различной конфигурации в зависимости от их габаритных размеров может быть вычислена по формулам, приведенным в табл. 35. Вывод этих формул дается в работе [7].[ …]
В работах [60, 61] высказывается мнение, что площадь гофрированного фильтрующего элемента может увеличиваться только до определенных пределов, так как при дальнейшем росте числа гофров (что адекватно уменьшению шага между гофрами) возрастает гидравлическое сопротивление элемента, обусловленное преобразованием на стенке гофра гидродинамического пограничного слоя, приводящего к уменьшению ресурса работы элемента по предельно допустимому перепаду давлений.[ …]
Первый и второй члены правой части выражения (У.9) представляют собой соответственно безразмерные перепады давлений в пространстве между гофрами (в радиальном направлении) и на фильтрующей перегородке. Их можно обозначить, как критерии Эйлера Еи,р и Еиф, соответствующие перепадам давлений АрТр и Арф.[ …]
Решение одного из этих уравнений совместно с уравнением (У. 7) позволит определить геометрические параметры продольно-гофрированного фильтрующего элемента, обеспечивающие максимальный ресурс его работы при заданных габаритных размерах. Аналогично предлагается оптимизировать геометрические параметры фильтрующих элементов других конструкций.[ …]
7) позволит определить геометрические параметры продольно-гофрированного фильтрующего элемента, обеспечивающие максимальный ресурс его работы при заданных габаритных размерах. Аналогично предлагается оптимизировать геометрические параметры фильтрующих элементов других конструкций.[ …]
При определении эффективности применения фильтрующих пакетов, состоящих из нескольких цилиндрических элементов, предполагается, что составляющие пакет фильтрующие элементы вписываются в габаритные размеры большого фильтрующего элемента, имеющего одинаковый объем с фильтрующим пакетом, как это изображено на рис. 80 [62].[ …]
Таким образом, увеличение числа фильтрующих элементов в пакете более шести нецелесообразно, так как существенного увеличения площади фильтрующей перегородки при этом не происходит. При проектировании фильтрующих элементов ограничиваются обычно шестью цилиндрическими фильтрующими элементами.[ …]
Вернуться к оглавлению
РАСЧЕТ И КОНСТРУКТИВНЫЕ ПАРАМЕТРЫ ВОДООЧИСТНЫХ ФИЛЬТРОВ РАДИАЛЬНОГО ТИПА | Дзюбо
1. Журба М.Г. Очистка воды на зернистых фильтрах. Львов: Изд-во Львовского университета, 1980. 200 с.
Журба М.Г. Очистка воды на зернистых фильтрах. Львов: Изд-во Львовского университета, 1980. 200 с.
2. Аюкаев Р.И. Интенсификация работы водоочистных фильтров и совершенствование метода их расчета. Петрозаводск: ПГУ, 1985. 136 с.
3. Ярошевская Н.В., Кульский Л.А. Очистка воды фильтрованием с нестационарным изменением скорости // Химия и технология воды. 1989. № 3. С. 251–253.
4. Дзюбо В.В. Подготовка подземных вод для питьевого водоснабжения малых населенных пунктов Западно-Сибирского региона: автореф. дис. … докт. техн. наук. СПб., 2007. 37 с.
5. Дзюбо В.В., Алферова Л.И. Исследование необходимой высоты и продолжительности защитного действия загрузки фильтров обезжелезивания подземных вод // Водоочистка.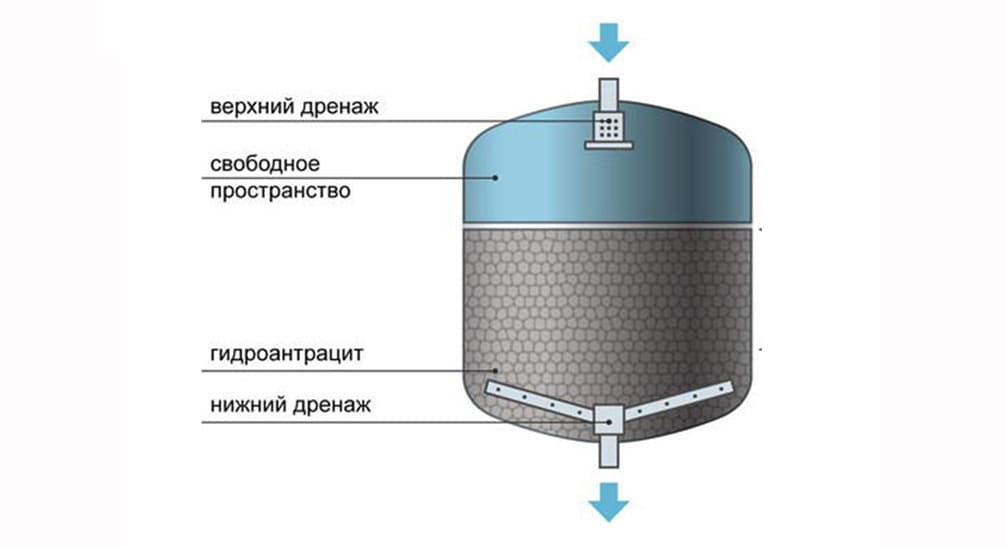 2007. № 8. С. 5–8.
2007. № 8. С. 5–8.
6. Дзюбо В.В. Расчет и сравнение грязеемкости загрузки фильтров, работающих в режиме постоянных и переменных скоростей // Вестник гражданских инженеров. 2009. № 4 (21). С. 68–72.
7. Дзюбо В.В., Алферова Л.И. Технологическое и конструктивное оформление радиального фильтрования природных вод // Вестник Томского государственного архитектурно-строительного университета. 2013. № 3. С. 329–344.
8. Дзюбо В.В., Алферова Л.И. Фильтрование природных вод в режиме неравномерных скоростей // Вестник Томского государственного архитектурно-строительного университета. 2007. № 2. С. 180–190.
9. Дзюбо В.В. Радиальные фильтры обезжелезивания подземных вод. Инженерные и технологические решения // Сантехника. 2006. № 4. С. 16–19.
2006. № 4. С. 16–19.
10. Дзюбо В.В. Радиальные фильтры обезжелезивания подземных вод. Конструктивные решения // Сантехника. 2006. № 5. С. 6–10.
11. Дзюбо В.В., Алферова Л.И. Роль массообменных характеристик фильтрующих материалов в процессе очистки подземных вод // Энергосбережение и водоподготовка. 2006. № 5. С. 21–24.
12. Дзюбо В.В. К вопросу определения высоты и грязеемкости загрузки фильтров обезжелезивания подземных вод // Сантехника. 2007. № 4. С. 4–7.
ФИЛЬТРЫ НА ПАВ С ВЫСОКОЙ ВХОДНОЙ МОЩНОСТЬЮ: БАЗОВЫЕ МОДЕЛИ ДЛЯ АНАЛИЗА ЭЛЕКТРОДНЫХ СТРУКТУР
Анализируются базовые модели дельта-функций, эквивалентных схем и Р-матриц фильтров на поверхностных акустических волнах (ПАВ) на СВЧ. На их основе разработано программное обеспечение для расчета всех типов базовых конструкций фильтров на ПАВ с высокой входной мощностью для систем специальной связи, радиолокационной и телекоммуникационной аппаратуры.
На их основе разработано программное обеспечение для расчета всех типов базовых конструкций фильтров на ПАВ с высокой входной мощностью для систем специальной связи, радиолокационной и телекоммуникационной аппаратуры.
Введение.
Важнейшей задачей при разработке любого устройства на поверхностных акустических волнах (ПАВ) является точность моделирования элементов, входящих в его структуру. Поскольку встречно-штыревые преобразователи (ВШП) являются основными элементами любого фильтра на ПАВ, очень важно иметь адекватную физическую модель преобразователя. До середины 1980-х годов основными методами расчета преобразователей с малым уровнем отражений были модель дельта-функций [1] и квазистатическое приближение [2]. Серьезным преимуществом первой модели является то, что на частотные свойства ВШП решающее влияние оказывают только его периодичность, число δ-источников и распределение максимального значения интенсивности источников, а не закон распределения электроупругого поля.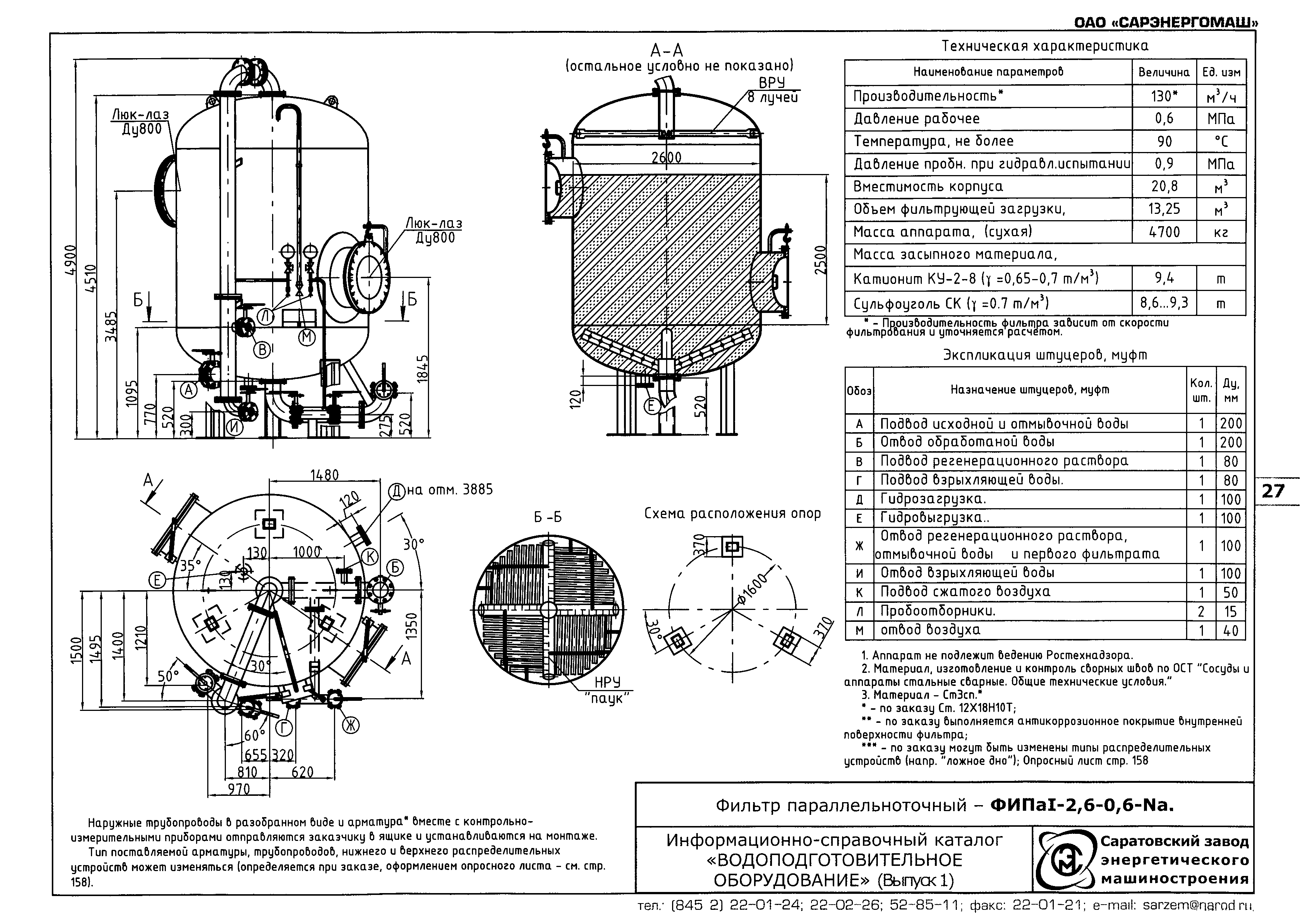 Второй метод, основанный на использовании функции Грина для описания поверхностного потенциала, является более точным.
Второй метод, основанный на использовании функции Грина для описания поверхностного потенциала, является более точным.
Данные методы обеспечивают удовлетворительную сходимость результатов при расчете трансверсальных фильтров различных методов взвешивания и конструкций [3]. Однако они непригодны для анализа структур с ненулевым уровнем отражений, на которых обычно реализуются ПАВ-фильтры с малыми потерями: на основе продольно-связанных резонаторных структур [4], на основе U-образного [5] и реверсивного [6] многополосковых ответвителей, структур импедансного типа [7,8], поскольку в них не учитываются влияние массовой нагрузки и эффект электрического закорачивания поля.
Необходимость расчета структур, работающих на основе внутренних отражений, обусловила необходимость разработки двумерной физической модели, учитывающей влияние масс-электрического нагружения на характеристику преобразователя [9]. Математический анализ таких структур до последнего времени был связан с большими трудностями, поскольку для точного моделирования характеристик требовался учет различных вторичных факторов. Использование теории связанных мод (coupling-of-modes-COM) для анализа преобразователей ПАВ, впервые предложенной К. Хартманом [10] и В. Райтом [11] и получившей развитие в работах советских, а затем российских авторов, существенно упростило задачу. Основными достоинствами этой модели являются простая математическая интерпретация, точное моделирование эффектов отражения внутри преобразователя, отказ от использования модели эквивалентной цепи при расчете параметров ВШП.
Использование теории связанных мод (coupling-of-modes-COM) для анализа преобразователей ПАВ, впервые предложенной К. Хартманом [10] и В. Райтом [11] и получившей развитие в работах советских, а затем российских авторов, существенно упростило задачу. Основными достоинствами этой модели являются простая математическая интерпретация, точное моделирование эффектов отражения внутри преобразователя, отказ от использования модели эквивалентной цепи при расчете параметров ВШП.
Данные методы использованы для разработки САПР фильтров на ПАВ любой сложности на разных стадиях этапа проектирования [12,13].
Модель дельта-функций.
Предварительный анализ фильтров на ПАВ осуществляется с использованием модели δ-функций. Материал подложки, эффекты второго порядка, пространственная протяженность электродов и т.д. в данной модели не учитываются.
В простейшем случае фильтр на ПАВ состоит из двух встречно-штыревых преобразователей – входного и выходного. Источником ПАВ является зазор между соседними электродами. Перекрытие между соседними электродами называется весом источника. Каждому источнику ПАВ ставится в соответствие δ-импульс, расположенный в центре источника и умноженный на соответствующий вес (весовой коэффициент).
Источником ПАВ является зазор между соседними электродами. Перекрытие между соседними электродами называется весом источника. Каждому источнику ПАВ ставится в соответствие δ-импульс, расположенный в центре источника и умноженный на соответствующий вес (весовой коэффициент).
Модель основана на использовании прямого (1) и обратного (2) дискретного преобразования Фурье (ДПФ и ОДПФ).
где s(n) — n-й весовой коэффициент.
Выражение для ДПФ ставит в соответствие N отсчетам сигнала s(n) N отсчетов спектра S(k).
Амплитудно-частотную характеристику (АЧХ) ВШП можно получить при помощи модифицированного прямого дискретного преобразования Фурье:
где fi – текущая частота; f0 – центральная частота ВШП; S(fi) – комплексная передаточная функция ВШП на текущей частоте.
АЧХ H(fi)=|S(fi)|или в децибелах 20lg|S(fi)|.
Фаза φ(fi) = arg (S(fi)) сигнала равна аргументу комплексного числа.
Групповое время запаздывания (ГВЗ)
Модель дельта-функций обычно используется на начальном этапе разработки устройства на ПАВ.
Модель эквивалентных схем.
В качестве базовой модели для анализа фильтров на ПАВ, в том числе на материалах с естественной однонаправленностью, используется модель эквивалентных схем. В этой модели ВШП разбивается на элементарные ячейки, каждая из которых описывает фрагмент звукопровода между центрами соседних электродов (рис.1).
Рис. 1. Модель базовой ячейки преобразователя
Каждая элементарная ячейка представляется в виде эквивалентной схемы шестиполюсника, которая описывается матрицей размерности 3×3, связывающей токи и напряжения структуры. Элементы матрицы элементарной ячейки определяются по правилам расчета электрических цепей, исходя из электрофизических свойств материала звукопровода:
где Z − характеристическое сопротивление среды для свободной и металлизированной Z = Zim поверхностей; θ – угол, на который смещается фаза волны за время прохождения участка; r − коэффициент трансформации, описывающий преобразование электрического сигнала в акустическую волну и наоборот.
Комплексная проводимость B = ReB + Im B позволяет учесть эффекты второго порядка, такие как рассеяние (определяется значением ReB) и накопление энергии (ImB) на границе металл – свободная поверхность. Коэффициент отражения волны на границе может быть рассчитан по формуле:
Указанные эффекты второго порядка, как правило, зависят от относительной толщины электродов, т.е. являются частотно-зависимыми. В модели эти зависимости описываются полиномами. Например, полиномы, передающие эффекты отражения, распространения и накопление энергии, имеют вид
где λ − текущая длина волны; h − толщина электродного покрытия.
Коэффициенты полиномов определяются для различных материалов и типов волн, как правило, экспериментальным путем по результатам испытаний тестовых устройств.
После вычисления матриц шестиполюсников каждой элементарной ячейки для заданного частотного диапазона эти матрицы последовательно сворачиваются (перемножаются). В результате получается матрица комплексных проводимостей фильтра:
В результате получается матрица комплексных проводимостей фильтра:
Комплексная передаточная функция K может быть найдена по формуле
где Rl и Rg− сопротивление нагрузки и источника сигнала соответственно.
Зная передаточную функцию, можно найти комплексную АЧХ фильтра:
а также фазу и характеристику группового времени замедления (ГВЗ).
Преимущество данной модели перед аналогичными моделями состоит в том, что эквивалентные параметры базовых ячеек определяются положением границ электродов. Это позволяет моделировать электродные структуры произвольной конфигурации. Такая гибкость модели обеспечивает возможность ее применения при синтезе различных типов ВШП.
Модель P-матриц.
В основе СОМ-метода [14], предложенного К.Хартманом и В.Райтом используется ряд допущений. Так, при анализе рассматривается преобразователь с малым уровнем потерь, имеющий равномерную структуру и одинаковую величину перекрытия электродов (рис. 2). Также, для упрощения, вводится допущение, что уровень переотражений мал. Тогда, дифференциальные СОМ-уравнения, описывающие распространение волны в электродной структуре, имеют вид:
2). Также, для упрощения, вводится допущение, что уровень переотражений мал. Тогда, дифференциальные СОМ-уравнения, описывающие распространение волны в электродной структуре, имеют вид:
Рис.2. Модель ВШП, используемая в СОМ-теории
СОМ-переменными являются: R(x, ω)- поверхностная волна в прямом направлении, S(x, ω) — поверхностная волна в обратном направлении, V0(ω) — потенциал преобразователя и I(x, ω) — ток в подводящих шинах. Тогда как СОМ-параметры это: α(k) — амплитуда преобразования, Фα(k)- фаза преобразования, ΛТ — период преобразователя, L — длина преобразователя, CE — электростатическая емкость на период преобразователя, ω — круговая частота, λ — длина волны ПАВ, VR — фазовая скорость волны. X0 — это начальная точка отсчета по оси Х, k0 — волновое число, n — номер гармоники. Обычно СОМ-анализ проводят для фундаментальной моды, что соответствует n=1.
Решение системы дифференциальных уравнений (9-11) может быть найдено при выполнении условия:
Представляет интерес использование Р-матриц для решения СОМ-уравнений. При этом акустические порты рассматриваются как порты отражения, а электрический порт совпадает с адмитансным. Как показано на рис.2, акустические порты расположены на краях преобразователя с координатами для левого порта и для правого порта. Поскольку электрический порт расположен на левом краю преобразователя, то ток в преобразователе привязан к координате . Р-матрица показывает связь выходящих акустических волн и тока с входящими акустическими волнами и потенциалом преобразователя:
При этом акустические порты рассматриваются как порты отражения, а электрический порт совпадает с адмитансным. Как показано на рис.2, акустические порты расположены на краях преобразователя с координатами для левого порта и для правого порта. Поскольку электрический порт расположен на левом краю преобразователя, то ток в преобразователе привязан к координате . Р-матрица показывает связь выходящих акустических волн и тока с входящими акустическими волнами и потенциалом преобразователя:
При записи решений СОМ-уравнений удобно ввести величину, показывающую отстройку от центральной частоты волнового вектора:
Тогда решение матрицы проводимости для однородного преобразователя с малым уровнем внутренних отражений имеет вид:
Поскольку ПАВ-фильтры с малым вносимым затуханием в основном реализуются на сильных пьезоэлектриках, для которых уровень переотражений не равен нулю, то дальнейшее развитие СОМ-теории было связано с определением коэффициентов отражения (P11) и пропускания (P12) преобразователя, как функции коэффициента отражения от электрода [15]:
где параметр Δ определяет частотную отстройку относительно центральной частоты ωс, k – коэффициент отражения от пары электродов, а L – длина отражающей структуры.
Развитие аппаратуры передачи, обработки и приема информации нового поколения существенно ужесточило требования к таким параметрам ПАВ-фильтров как уровень вносимого затухания и прямоугольность АЧХ, и как следствие, привело к усложнению исходной модели преобразователя ПАВ. Например, в работе [16] учтена дисперсия скорости волны от частоты и потери на распространение γp.
В последние годы для анализа прецизионных высокоизбирательных фильтров на ПАВ с малым вносимым затуханием используется модифицированный СОМ-метод, в котором параметры структуры на ПАВ в целом (ВШП, отражающей структуры или их произвольной комбинации) определяются перемножением соответствующих Р-матриц отдельных электродов (как это делается в обычной теории четырехполюсников с использованием матрицы рассеяния) [17]. Этот метод позволяет учитывать изменяющийся период структуры, аподизацию и неоднородное распределение поверхностного заряда на электродах структуры и он более перспективен с точки зрения дальнейшего усложнения исходной модели структуры.
Пусть задана ПАВ-структура в виде электродов с чередующейся полярностью, произвольно меняющимся периодом и перекрытием соседних электродов. Также предполагаем, что источник сигнала U0 подключен слева. Рассмотрим k-й электрод ВШП (рис. 3). Пусть R(Z,w) и S(Z,w) – две связанные между собой плоские волны с волновым числом k, распространяющиеся в электродной структуре ВШП. Причем R(Z,w) распространяется в направлении оси Z, а S(Z,w) – в направлении, противоположном оси Z. Тогда однородные плоские волны можно записать в виде
где R(w) и S(w) – комплексные амплитуды соответствующих волн.
Рис. 3. k-электрод ВШП
Пусть на k-й электрод слева падает волна RK(R,w), а справа – SK+1(Z,w). Тогда для комплексных амплитуд прошедших волн с учетом механизмов отражения, прохождения и преобразования с коэффициентом εK можно получить уравнения
Тогда для комплексных амплитуд прошедших волн с учетом механизмов отражения, прохождения и преобразования с коэффициентом εK можно получить уравнения
Фазовые сомножители у слагаемых, связанных с отражением (преобразованием) волн, определяют фазовый набег от центра отражения (преобразования) волны до соответствующей границы: ZK – для SK(w) и ZK+1 — для RK(w). Центр отражения (преобразования) ПАВ принят находящимся в центре электрода. Вычислим эффективное волновое число:
где rK – комплексный коэффициент отражения от k-го электрода; kЕ – эффективное волновое число ПАВ; k0 = 2p/pK; pK= ZK+1–ZK; xK – коэффициент преобразования ПАВ на k-м электроде; h1K=W1K/W0; h2K=W2K/W0;W0 – максимальная апертура; W1K – перекрытие соседних электродов; W2K=W0 в случае, если используются холостые электроды; W2K=W1K, если холостые электроды не используются.
kЕ = 2p / lE=w /(V0 + LK (VM – V0)/pK) – ja,
где V0 – скорость ПАВ на свободной поверхности; VM – скорость ПАВ под металлизированной поверхностью; a – суммарные потери на распространение ПАВ в электродной структуре на единицу длины.
Изменение тока в шине ВШП происходит за счет преобразования прямой и обратной волн и падения напряжения на емкости электрода
Рассмотрим слагаемые, связанные с преобразованием ПАВ при прохождении через электрод ВШП (рис.3), с учетом того, что возбуждение носит распределенный характер. Будем полагать, что прямое и обратное преобразование волны на электродах происходит с одинаковой эффективностью, т.е. носит взаимный характер. Пусть задано распределение поверхностного тока на электродах ВШП в виде J(Z). Будем считать, что механизм преобразования ПАВ малым участком поверхностного тока DZK электрода и всего электрода аналогичны. Тогда, просуммировав вклады и преобразование ПАВ по ширине электрода относительно его центра ZCK и переходя к пределу (ΔZK→ 0), получим
Будем считать, что механизм преобразования ПАВ малым участком поверхностного тока DZK электрода и всего электрода аналогичны. Тогда, просуммировав вклады и преобразование ПАВ по ширине электрода относительно его центра ZCK и переходя к пределу (ΔZK→ 0), получим
Соотношения (24) – (26) можно записать в матричной форме:
где Ga– акустическая проводимость излучения на частоте синхронизма.
Используя систему уравнений (24)–(26) с произвольными коэффициентами, записанную для двух последовательно включенных ПАВ-структур, нетрудно получить компоненты суммарной P-матрицы:
Теперь P-матрица ВШП в целом может быть найдена последовательным перемножением P-матриц, описывающих каждый электрод.
где P0 = 1–P(2)(1,1) P(1)(2,2). Верхние индексы s, 1 и 2 относятся, соответственно, к суммарной P-матрице, Р-матрице ПАВ-структуры, находящейся слева, и Р-матрице ПАВ-структуры, находящейся справа.
ПАВ-структура может представлять собой отдельный электрод или группу электродов, для которой вычислена суммарная Р-матрица. При этом соотношения (29)–(37) позволяют рассчитывать входную проводимость P(3,3) ВШП в составе фильтра или резонатора с произвольно меняющимся периодом и апертурой электродов вдоль структуры ВШП и реальным распределением поверхностного тока (заряда) на электродах ВШП.
Для отражающих структур расчет компонентов Р-матрицы производится при выполнении условий, что xK= 0, U= 0 и С2 = 0. При этом элементы матрицы Р (1,3), Р(2,3), Р (3,1), Р (3,2), Р (3,3) будут равны нулю.
Р-матрица, описывающая зазор между ВШП и отражательной структурой, может быть получена из соотношений (24)–(26) при условиях xK= 0, U= 0 и С2 = 0, rK=0 и WK= 0.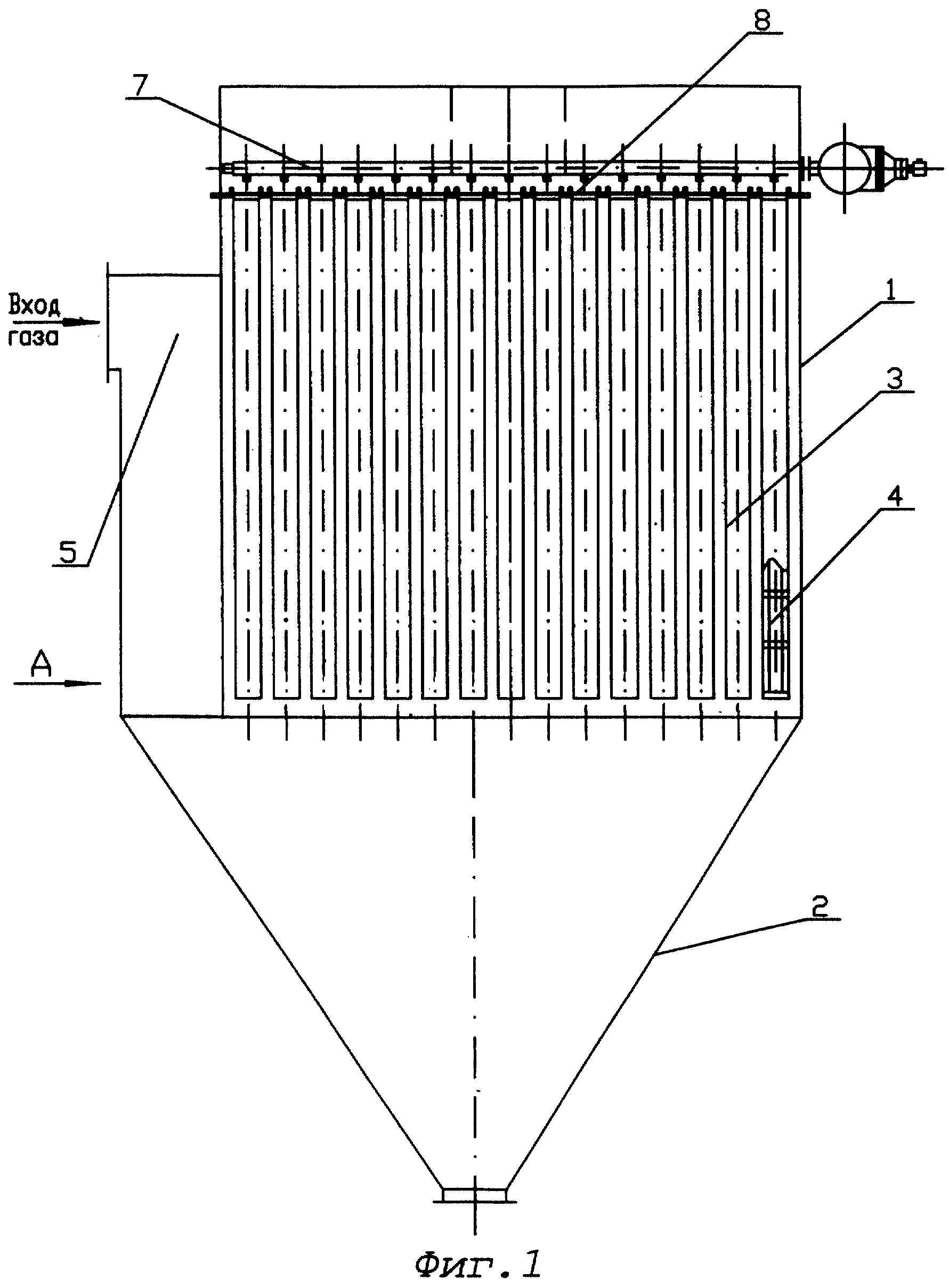 В этом случае ненулевыми будут только элементы Р-матрицы Р(1,2), Р(2,1). Учет фазовой задержки при распространении волны в зазоре осуществляется путем умножения амплитуд падающих и выходящих волн на exp(-jkd), где d – расстояние между ВШП и отражающей структурой. Расчет проводимости фильтра в целом осуществляется путем перемножения соответствующих Р-матриц и решения суммарной системы уравнений (28) относительно токов в преобразователях.
В этом случае ненулевыми будут только элементы Р-матрицы Р(1,2), Р(2,1). Учет фазовой задержки при распространении волны в зазоре осуществляется путем умножения амплитуд падающих и выходящих волн на exp(-jkd), где d – расстояние между ВШП и отражающей структурой. Расчет проводимости фильтра в целом осуществляется путем перемножения соответствующих Р-матриц и решения суммарной системы уравнений (28) относительно токов в преобразователях.
Данный подход был использован при разработке программного обеспечения для расчета всех типов базовых конструкций фильтров на ПАВ с высокой входной мощностью.
Заключение.
Приведенные базовые модели для расчета электродных структур позволяют рассчитать фильтры на ПАВ любой сложности, в том числе с ненулевым уровнем отражений. Исключение составляют трансверсальные фильтры с апертурой преобразователей менее 10 длин волн и резонаторные поперечно-связанные узкополосные ПАВ-фильтры, для точного расчета которых необходимо дополнительно учитывать эффекты волноводного распространения поверхностной акустической волны [18].
Литература.
- Hartmann C.S., Bell D.T., Rosenfeld R.S. Impulse model design of acoustic surface wave filters. IEEE Trans., MTT-21, № 4, p. 162-175, 1973.
- Багдасарян А.С. Исследование преобразователей с амплитудной модуляцией поверхностных акустических волн и разработка фильтров на их основе автореферат диссертации на соискание ученой степени кандидата технических наук, М. Институт радиотехники и электроники АН СССР
- Багдасарян А., Синицына Т., Иванов П., Швец В. Частотно-селективные СВЧ-модули на основе преобразователей веерного типа Электроника: Наука, технология, бизнес. 2012.№ 2 (116). С. 066-071.
- Синицына Т.В., Багдасарян А.С., Егоров P.B. ПАВ-фильтры на основе продольно-связанных структур. Электронная промышленность. 2004. № 1. С. 14.
- Багдасарян А.С., Синицына Т.В., Машинин О.В. ПАВ-фильтры с малыми потерями на основе U-образного ответвителя. Электросвязь. 2004. № 2.
 С. 32.
С. 32. - Синицына Т.В., Багдасарян А.С., Кузнецов М.В Резонаторные ПАВ-фильтры на основе реверсивного МПО. Системы и средства связи, телевидения и радиовещания. 2003. № 1-2. С. 15.
- Багдасарян А.С., Карапетьян Г.Я. Импедансные ПАВ фильтры для спутникового телевидения и телевидения высокой четкости. Электросвязь, №6, 1998 г., с.21-22.
- Багдасарян А., Багдасарян С., Карапетьян Г., Машинин О., Синицына Т. Импедансные ПАВ-фильтры для телекоммуникационных систем. Российский приоритет. Электроника: Наука, технология, бизнес. 2014. № 7 (139). С. 48-65.
- Багдасарян А.С., Синицына Т.В. Селективные акустоэлектронные приборы на основе однонаправленных структур поверхностных акустических волн, Монография, Москва, 2004, 103 с.
- S. Hartman A fast accurate method for calculating the SAW and bulk wave radiation admittance of a SAW transducer Proc. IEEE Ultrason. Symp. 1988, p.39-46 Wright P.V., A new generalized modeling of SAW transducers and gratings, Proc.
 43rd Annual Symp. Freq. Control, 1989, p.596-605
43rd Annual Symp. Freq. Control, 1989, p.596-605 - Wright P.V., A new generalized modeling of SAW transducers and gratings, Proc. 43rd Annual Symp. Freq. Control, 1989, p.596-605
- Багдасарян А., Синицына Т., Машинин О., Иванов П., Егоров Р.
Устройства частотной селекции на ПАВ в современных системах связи, радиолокации и телекоммуникации. Электроника: Наука, технология, бизнес. 2013.№ 8 (131). С. 128-136. - Гуляев Ю., Багдасарян А.С., Синицына Т.В., Машинин О.В., Прапорщиков В.В., Орлов М.М., Егоров Р.В. ПАВ-фильтры во входных каскадах приемо-передающих устройств. Наука и технологии в промышленности. 2006. № 4. С. 82.
- Багдасарян А.С., Синицына Т.В. Анализ ВШП методом связанных мод. Системы и средства связи, телевидения и радиовещания. 2003. № 1-2. С. 11.
- Plessky V.P., A simple two parameter coupling-of-modes model for shear SAW propagating in periodic gratings, Proc. IEEE Ultrason. Symp. 1993, p.63-67
- Синицына Т.
 В. Исследование и разработка физических методов проектирования высокоизбирательных акустоэлектронных приборов с малым вносимым затуханием диссертация на соискание ученой степени кандидата технических наук автореферат диссертации на соискание ученой степени кандидата технических наук / Москва, 2003/
В. Исследование и разработка физических методов проектирования высокоизбирательных акустоэлектронных приборов с малым вносимым затуханием диссертация на соискание ученой степени кандидата технических наук автореферат диссертации на соискание ученой степени кандидата технических наук / Москва, 2003/ - Дмитриев В.Ф. Развитие теории и методов расчета устройств на поверхностных акустических волнах для обработки радиосигналов, диссертация на соискание ученой степени доктора технических наук / С. Петербург, 2004/
- Багдасарян А.С., Гуляев Ю.В., Никитов С.А., Багдасарян С.А., Синицына Т.В., Бутенко В.В., Машинин О.В., Прапорщиков В.В. Узкополосные фильтры на поверхностных акустических волнах в системах радиочастотной идентификации Радиотехника и электроника. 2008. Т. 53. № 7. С. 887-896.
Разработка и исследование полосковых фильтров короткого см диапазона волн
АННОТАЦИЯ
Одним из требований к передающим радиотехническим устройствам является обеспечение заданного уровня паразитных излучений на частотах гетеродина и зеркальной частоте. Обычно для решения этой задачи используются полосно-пропускающие фильтры, настроенные на рабочую полосу передатчика. В статье рассмотрены различные варианты таких фильтров и особенности их расчета. Приведены экспериментальные результаты.
Обычно для решения этой задачи используются полосно-пропускающие фильтры, настроенные на рабочую полосу передатчика. В статье рассмотрены различные варианты таких фильтров и особенности их расчета. Приведены экспериментальные результаты.
ABSTRACT
One of the requirements for transmitting radio devices is to provide a given level of parasitic radiation at the frequencies of the local oscillator and the image frequency. Usually, this problem is solved by bandpass filters tuned to the working band of the transmitter. In the article various variants of such filters and features of their calculation are considered. Experimental results are presented.
Ключевые слова: компьютерный расчет, СВЧ, фильтр, полоса пропускания.
Keywords: computer aid design, microwaves, filter, passband.
Постановка задачи
Для обеспечения необходимого уровня побочных излучений передатчика необходим полосно-пропускающий фильтр, подавляющий излучение гетеродина и излучение на зеркальной частоте применяемого преобразователя частоты. При этом фильтр должен с допустимыми потерями пропускать сигнал на рабочей частоте. Для разрабатываемого нами передатчика с рабочей частотой 8.4 ГГц потребовался фильтр со следующими параметрами:
При этом фильтр должен с допустимыми потерями пропускать сигнал на рабочей частоте. Для разрабатываемого нами передатчика с рабочей частотой 8.4 ГГц потребовался фильтр со следующими параметрами:
Полоса пропускания на 8.4 ГГц >50 МГц,
Подавление на частоте гетеродина 7.4 ГГц > 60 дБ.
Потери в полосе пропускания <10 дБ
КСВН в полосе пропускания < 2
Размеры печатной платы ограничивались из конструктивных соображений 49 х 18 мм. Толщина платы выбиралась в зависимости от типа и конструкции фильтра.
Рассматривались две возможные конструкции фильтров:
а) фильтры на диэлектрических резонаторах с большой диэлектрической проницаемостью;
б) фильтры на полосковых линиях.
Расчёт в среде CST Microwave Studio (CST) [2] фильтров с диэлектрическими резонатороми (эпсилон =40) показал, Рис.1, что, при одинаковом подавлении с полосковыми, они имеют в разы меньшие полосы пропускания, что затрудняло использование фильтра.
Рисунок 1. Расчётные S- параметры: S11 и S21 фильтра с диэлектрическими резонаторами
Кроме того, конструктивно было удобнее использовать фильтр на полосковых линиях. Поэтому далее разрабатывались полосковые фильтры.
Варианты исполнения полосковых фильтров
Сначала были рассмотрены фильтры на симметричной полосковой линии в прямоугольном корпусе, заполненным материалом Rogers RO4350B. Были разработаны и рассчитаны на CST несколько фильтров, различающихся числом звеньев.
На рис. 2 показана топология фильтра с четырьмя звеньями, а на рис. 3 – рассчитанные S-параметры.
Рисунок 2. Печатная плата с полосковым 4-х звенным фильтром
Рисунок 3. Расчётные S-параметры: S11 и S12 полоскового 4-х звенного фильтра
При расчетах задавались следующие параметры:
- тангенс потерь в подложке 0.
 7 См/м.
7 См/м.
При расчёте в CST использовалось авторегрессивный программный фильтр (AR‑фильтр), предназначенный для расчёта узкополосных устройств, имеющих большое время затухания возбуждающего сигнала. Для примера, на рис.3 показан расчёт, сделанный без применения AR-фильтра. Видно, что результаты расчётов на рис. 3 и рис. 4 сильно различаются. Измерения показали, что реальные характеристики близки к рассчитанным с AR- фильтром.
Конструкция фильтра представляла собой подложку с полосками, помещенную в прямоугольный корпус, снабженный коаксиальными разъёмами.
Испытания изготовленного фильтра проводились с помощью панорамного измерителя КСВН типа Р2-137. Измерения показали, что характеристики фильтров сильно отличаются от расчётных и не удовлетворяют техническим требованиям. Главное, что подавление сигнала на заданной частоте гетеродина (7.4 ГГц) и в полосе от 6 до 10 ГГц (исключая полосу пропускания), оказалось значительно меньше требуемого.
Рисунок 4. Расчётные S-параметры полоскового фильтра, сделанные без использования AR-фильтра
Расчётные S-параметры полоскового фильтра, сделанные без использования AR-фильтра
В результате проведенного анализа были выявлены недостатки в разработанной конструкции фильтра. Основным из них была большая ширина корпуса, в который помещалась подложка с фильтром. В результате, в полученном волноводе могли распространяться высшие, волноводные типы волновод [3]. Подавление паразитных сигналов могло уменьшиться из-за преобразования основного типа волны полосковой линии (TEM) в волноводные моды колебаний. Эти моды могли проходить через фильтр с относительно малыми потерями. Причиной возникновения волноводных мод могли быть неоднородности и отклонения от симметрии в СВЧ тракте.
Введение поглотителя в критичные места тракта с целью ослабить волноводные типы, позволило увеличить подавление, но оно оставалось значительно меньше расчётного.
Вторым недостатком фильтра были большие измеренные потери в полосе пропускания — 5.5 дБ (расчетная величина 5. 1 дБ).
1 дБ).
Для устранения этих недостатков были внесены изменения в конструкцию фильтров. Для исключения распространения в корпусе волноводных типов волн была уменьшена ширина корпуса, что сделало волновод запредельным. Для этого пришлось повернуть полоски фильтра под углом к оси корпуса, как показано на рис. 5. Скосы углов на полосках сделаны, чтобы дополнительно уменьшить ширину волновода и увеличить его запредельность.
Рисунок 5. Печатная плата с исследуемым полосковым фильтром
Для уменьшения потерь в полосе пропускания из корпуса была удалена большая часть подложки, вносящей потери, а в середине корпуса оставлена тонкая плата из материала Rogers с печатными полосками. Толщина платы составляла 0.25 мм. В результате получился фильтр на подвешенной полосковой линии с воздушным заполнением.
При переходе к полосковой линии с воздушным заполнением увеличилась длина волны в полосковой линии [1]. Поскольку длина корпуса фильтра определялось конструкцией прибора и не изменилась, пришлось уменьшить число звеньев фильтра.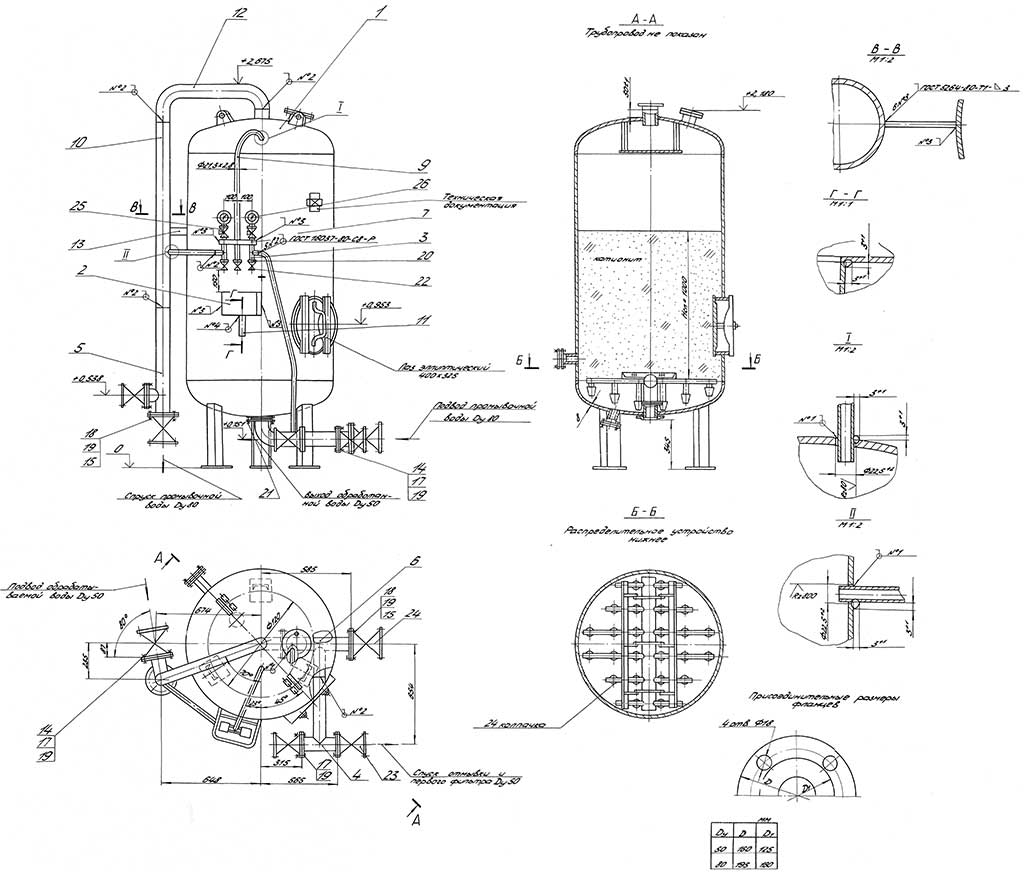
Кроме фильтра с параллельными четвертьволновыми полосками, были разработаны также фильтры с полосками встык, показан на рис. 6.
Рисунок 6. Печатная плата полоскового фильтра с полосками, расположенными вдоль оси
Фильтры с полосками встык позволяют дополнительно уменьшить ширину корпуса и увеличить запредельность волновода. Однако на заданной длине корпуса помещались только 2 ступени фильтров, поэтому они имели меньшее подавление, чем фильтры с наклонными полосками, имеющими большее количество звеньев.
Особенности расчета фильтров
Сначала расчёт фильтров проводился по методике, изложенной в [4,5]. Полученные из расчётов размеры зазоров между полосками использовались как исходные для расчётов в CST. Как правило, рассчитанные фильтры имели большой КСВН и требовалась дополнительная оптимизация размеров, которая проводилась вручную, перебором, исходя из выявленных зависимостей КСВН от размеров.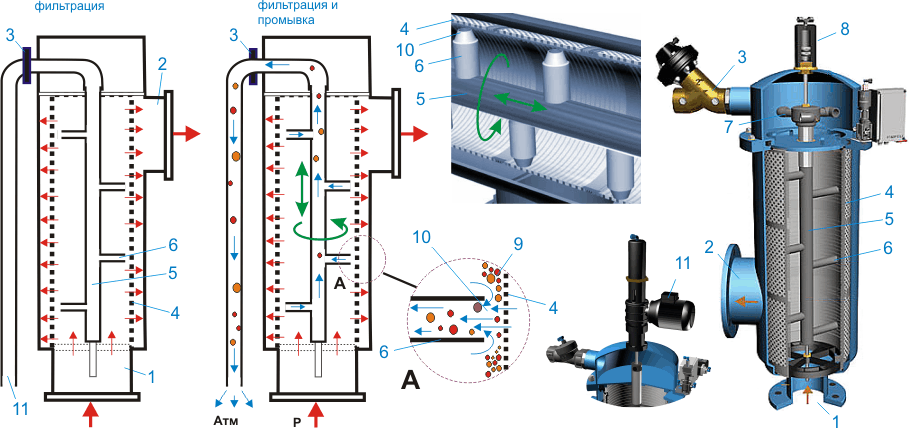 В случае многозвенных фильтров это занимало много времени, но было эффективнее, чем использование заложенной в CST опции оптимизации.
В случае многозвенных фильтров это занимало много времени, но было эффективнее, чем использование заложенной в CST опции оптимизации.
В дальнейшем, для получения исходных размеров фильтра для последующих расчетов в CST, использовались размеры, полученные в среде AWR Design Environment (AWR). В AWR расчёт размеров фильтра по заданным характеристикам производится очень быстро, а в CST занимает много времени. Но AWR предназначена для расчёта плоских структур. В CST, в отличие от AWR, можно сделать объёмный чертеж устройства, близкий к реальной конструкции, и выполнить расчёт именно для нее. Поэтому размеры, полученные в AWR, подставлялись в чертёж CST и производился дальнейший расчет. Оказалось, что при использовании AWR требовалась меньшая коррекция размеров в CST для оптимизации КСВН.
Одной из основных задач работы была проверка соответствия рассчитанных на CST и реальных характеристик фильтров. Определялись оптимальные настройки программы, позволяющие получить достаточно точные результаты при небольшом времени расчётов.
Остановимся на некоторых особенностях расчёта в CST.
В процессе расчёта были введены следующие элементы настройки, повышающие точность расчёта:
1) при анализе в CST устройств с высокой добротностью при работе с временным решателем Т-решатель (Transient solver) необходимо применять AR- фильтр, который сильно повышает точность расчётов;
2) первые расчёты фильтров с полосками, параллельными оси фильтра (см. рис.2), проводились с Т-решателем. Но при переходе к фильтрам с наклонными полосками (рис. 5), время счёта резко увеличилось. Для его уменьшения мы перешли к использованию частотного решателя F-Solver. Использовалась опция для расчёта узкополосных фильтров Resonant: Fast S-parameters. Время расчёта значительно уменьшилось. В F-Solver хорошо считаются и фильтры с полосками, параллельными оси фильтра. Результаты расчёта в Т и F решателях были близки, но точно не совпадали, в частности, значения центральной частоты фильтра.
3) для точных расчётов необходимо применять заложенный в программе метод оптимизации разбиения области расчёта на ячейки. В последовательных проходах расчёта увеличивается и оптимизируется положение ячеек. Это приводит к увеличению точности, но и к большому увеличению времени счёта. Поэтому приходится выбирать некоторый компромисс между ними;
В последовательных проходах расчёта увеличивается и оптимизируется положение ячеек. Это приводит к увеличению точности, но и к большому увеличению времени счёта. Поэтому приходится выбирать некоторый компромисс между ними;
4) при расчётах в F-Solver часто возникали сообщения о появлении паразитных элементов (Suspecious elements). Они возникают при недостаточно мелком разбиении структуры на ячейки. При этом уменьшается точность и увеличивается время расчёта. Для устранения этих элементов, приходилось увеличить в настройках плотность ячеек;
5) при работе в частотном решателе F-Solver расчёт в опции Resonant: Fast S-parameters выполнялся только с идеальными металлами типа PEC. Учёт потерь в металлах, какими являются покрытия полосков и корпуса, можно сделать в опции General Purpous.
Сопоставление расчетных и экспериментальных данных
Рассчитанные на CST размеры фильтров использовались для изготовления чертежей в программе Inventor и последующего изготовления корпусов и печатных плат.
Были изготовлены полосковые фильтры нескольких типов: с параллельными полосками и полосками встык, с разными полосами пропускания и, соответственно, подавлением вне полосы, с разными величинами ширины полосков.
Измерения фильтров проводились на вектор-анализаторе VNA MS4644A.
В табл. 1 приведены результаты расчёта и измерений основных характеристик четырех изготовленных фильтров.
Таблица 1.
Результаты расчёта и измерений основных характеристик 4-х фильтров
|
N фильтра
|
1
|
2
|
3
|
4
|
|
Число звеньев
|
4
|
4
|
3
|
2 (встык)
|
|
Параметр
|
Расчет / результаты измерений
| |||
|
Fo, ГГц
|
8.
|
8.46 / 8.44
|
8.36 / 8.35
|
8.42 / 8.35
|
|
A(7.4), дБ
|
82 / 76
|
72 / 68
|
67 / 64
|
56 / 51
|
|
A(Fo), дБ
|
2.1 / 5.2
|
1.6 / 3.3
|
3.7 /3.4
|
3.5 / 3.4
|
|
S11(8.4), дБ
|
-16 / -14
|
-14 / -11
|
-9 / -17
|
-16 / -6
|
|
dF, МГц
|
180/200
|
300/320
|
400/370
|
100/130
|
Обозначения в табл.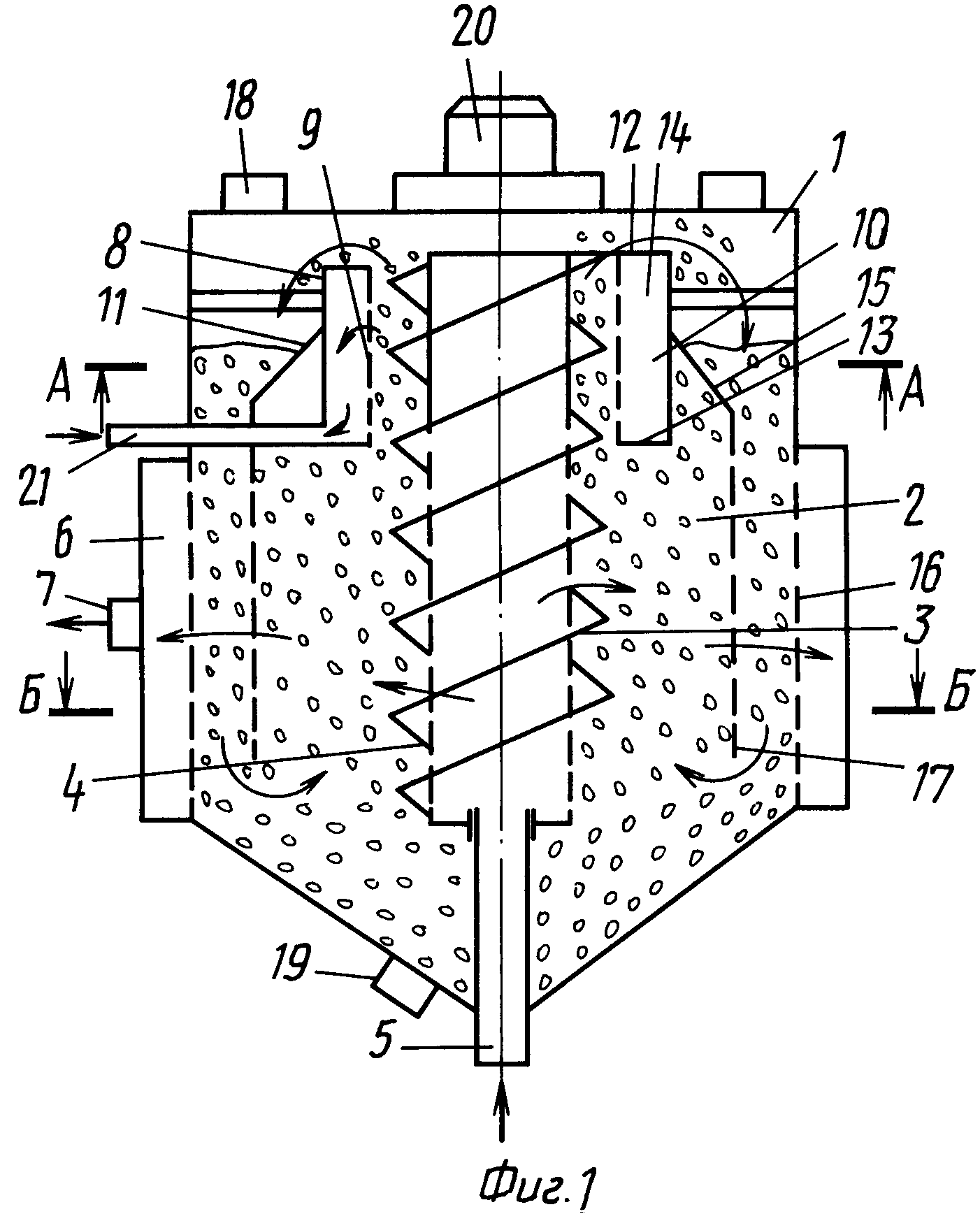 1:
1:
Fo — центральная частота полосы пропускания;
A(7.4) – подавление входного сигнала на частоте 7.4 ГГц
A(Fo) — ослабление входного сигнала на частоте Fo;
S11(8.4)-параметр S11 на частоте F=8.4 ГГц;
dF — полоса пропускания по уровню 3дБ.
Из табл. 1 видно, что нет полного совпадения расчетов и измерений, но результаты близки. Дальнейшая доработка фильтров возможна после измерений и внесения коррекции в размеры, с использованием расчётов в CST.
Далее приводятся более детальные результаты измерений одного из фильтров, №1 (с наибольшим подавлением на частоте 7.4 ГГц).
На рис. 7 и 8 приведены рассчитанные на CST и измеренные S-параметры S11, показывающие потери на отражение, и соответствующие коэффициенты стоячей волны (КСВН).
Рисунок 7. Расчётные и измеренные S11 – параметры фильтра №1
Рисунок 8. Расчётный и измеренный КСВН фильтра №1 в полосе пропускания
Обозначения на рис. 7 и 8: Р – расчёт, И – измерения.
Видно, что есть расхождения, но расчёт позволяет достаточно точно оценить центральную частоту и S11 фильтра.
На рис. 9 показаны расчётный и измеренные графики S — параметра S12, показывающие потери на проход.
Рисунок 9. Расчётные и измеренные S12- параметры фильтра №1
Обозначения на рис. 9:
Р- расчёт в опции F-Solver: Resonant: Fast S-par;
Р1 — расчёт в опции F-Solver: General purpose;
И — измерения.
Расчёты сделаны в CST, в решателе F-Solver в разных опциях: опции Resonant: Fast S-parameters, где учтены только потери в подложке, и опции General purpose, где учтены также потери в металлах покрытия (золота и никеля).
Видно, что есть отличия в значениях Fo при расчёте в разных опциях решателя. Это нужно учитывать при расчёте узкополосных устройств, когда требуется точное знание частоты.
На рис. 10 показаны потери на проход в полосе пропускания. Обозначения те же, что и на рис. 9.
Рисунок 10. Расчётные и измеренные потери фильтра №1 в полосе пропускания
Видно, что измеренные потери оказались значительно больше рассчитанных. Потери на проход в полосе пропускания в фильтрах №1 и №2 с четырьмя звеньями значительно превосходят расчётные, а в фильтрах №3 и №4 — близки к ним, что видно из Табл.1. Причина расхождения пока не определена.
Групповое время задержки
При использовании полосно-пропускающих фильтров в устройствах с преобразователями частоты в некоторых случаях нужно знать время групповой задержки в полосе пропускания. Например, когда в полосе пропускания есть коррелированные сигналы и в детекторе, на выходе приёмника, происходит сложение сигналов, симметричных центральной частоте приема. Для того, чтобы не было искажений, желательно, чтобы время задержки этих сигналов было постоянным или менялось линейно, чтобы было легко внести поправки при обработке сигналов.
Нами были рассчитаны и измерены времена задержки фильтров и рассчитана их производная по частоте.
На рис. 11 показаны расчётное и измеренное время групповой задержки сигналов.
Рисунок 11. Расчётное и измеренное время групповой задержки фильтра №1
Обозначения:
Р – расчёт,
И – измерения.
На рис. 12 показаны графики производной от времени задержки по частоте в полосе пропускания фильтра. Данные получены из расчётной и измеренной кривых. По этим графикам можно оценить сдвиг по фазе принимаемых сигналов, вызванный наличием фильтра.
Рисунок 12. Зависимость расчётной и измеренной скорости изменения времени групповой задержки от частоты
Обозначения:
Р – расчёт,
И – измерения.
Время задержки фильтров получилось значительно меньше предельно допустимых значений, приведенных в стандарте CCSDS 401.0-B [6], и, следовательно, разработанные фильтры могут быть использованы в передающих радиотехнических устройствах.
Заключение
Разработаны полосковые полосно-пропускающие фильтры на частоту 8.4 ГГц, предназначенные для работы в устройствах с преобразователем частоты. Фильтры применяются для подавления сигналов на частоте гетеродина и зеркальной частоты. Расчёты фильтров проводились с использованием программ AWR CST Microwave Studio и AWR Design Environment. Рассмотрены некоторые особенности расчёта в CST.
Чертежи корпуса и печатных плат выполнялись в программе Inventor. Измеренные характеристики получились достаточно близкими к рассчитанным. Расчёты на CST могут быть успешно использованы как для получения исходных размеров фильтра, так их коррекции после измерений характеристик фильтров. Изготовленные фильтры удовлетворяют заданным требованиям.
Конструкция и материалы фильтров позволяют применять их и на более высоких частотах.
Список литературы:
1. Гинзтон Э.Л. Измерения на см волнах. – М.: Изд. иностранной литературы, 1960. — 620 с.
2. Курушин А.А., Пластиков А.Н. Проектирование СВЧ устройств в среде CST Microwave Studio. – М.: Изда-тельство МЭИ, 2011. – 155 с.
3. Лебедев И.В.. Техника и приборы СВЧ. – М.: Высшая школа, 1970. – 440 с.
4. Маттей Д.Л., Янг Л., Джонс Е.М.. Фильтры СВЧ, согласующие цепи и цепи связи. – М.: Связь, 1971. – 222 с.
5. Фельдштейн А.Л., Явич Л.Р., Смирнов В.П.. Справочник по элементам волноводной техники. – М.: Совет-ское радио, 1967 — 651 с.
6. The Consultative Committee for Space Data Systems, Radio frequency and modulation systems – Part 1 Earth stations and spacecraft, Recommended Standard CCSDS 401.0-B, Blue Book, December 2013.
Конструкция сетчатых фильтров Yamit
Ниже приведены соображения, принимаемые в расчет при выборе конкретной модели (т.е. конструкции) фильтра.
Выбор фильтра может быть осуществлен специалистами фирмы YAMIT на основе многолетнего опыта применения на различных производствах всего мира. Но заказчик должен понимать и принимать технические, технологические и экономические критерии выбора конкретной модели фильтра.
ТЕХНОЛОГИЯ ОЧИСТКИ СЕТКИ
Существуют две базовые технологии автоматической и полуавтоматической очистки сетки фильтра («фильтры-грязевики» с ручной очисткой в этом разделе не обсуждаются) — это сканерная и щеточная технологии.
Критерии выбора:
- Сканерная очистка (рисунок слева).
- Рейтинг фильтрации загрязнений 10-800 мкм (0.01-0.8 мм) — оптимальная зона применения технологии. Но возможна очистка и значительно более крупных загрязнений.
- Отсутствие в фильтруемой жидкости значительного количества тяжелых нефтепродуктов.
- Отсутствие условий возникновения активных обрастаний сетки как химической, физической, так и биологической природы.
- Щеточная очистка (рисунок справа).
- Рейтинг фильтрации загрязнений 200-3000 мкм (0.2-3 мм) — оптимальная зона применения технологии. Но возможна очистка и значительно более крупных загрязнений.
- Присутствие в фильтруемой жидкости тяжелых нефтепродуктов (требуется тщательное изучение условий!).
- Возникновение активных обрастаний сетки как химической, физической, так и биологической природы.
В общем случае сканерная очистка дает более качественный и надежный результат. При этом отсутствует механический износ сетки и механизма очистки.
Сканерные фильтры имеют незначительно более высокую цену, но, при этом более низкие эксплуатационные расходы.
ТИП ПРИВОДА МЕХАНИЗМА ОЧИСТКИ СЕТКИ
Существуют две конструкции привода приводы механизма автоматической очистки сетки фильтра (фильтры с ручным приводом и «фильтры-грязевики» с ручной очисткой в этом разделе не обсуждаются) — это электрический и гидравлический приводы.
В производственной программе YAMIT есть практически идентичные конструкции, но с разным приводом механизма очистки.
Критерии выбора:
- Электрический привод (рисунки снизу).
- Низкое давление в трубопроводах (от 1 бар, но лучше более 1.5-2 бар).
- Требования к повышенной надежности системы.
- Возможность возникновения залповых выбросов загрязнений.
- Возможность использования электрической силовой сети.
- Применение щеточной технологии очистки. Щеточные фильтры могут быть только с электрическим и ручным приводом.
- Гидравлический привод (рисунки сверху).
- Относительное высокое давление в трубопроводе (от 2 бар, но лучше более 3-4 бар).
- Невозможность использования электрической силовой сети (поле) или высокая взрываопасность производства.
- Применение сканерной технологии очистки.
Электрический привод более дорогой, но дает более качественный и надежный результат.
КОНСТРУКЦИЯ СЕТКИ И РЕЙТИНГ ФИЛЬТРАЦИИ
Существуют три варианта исполнения фильтрующей сетки.
Критерии выбора:
- Плетеная сетка (рисунок справа).
- Очень тонкие рейтинги фильтрации (начиная от 10 мкм).
- Применение сканерной технологии очистки сеток.
Перфорированная сетка
- Сетки грубых рейтингов фильтрации (более 1-3 мм).
- Применение сканерной или щеточной технологии очистки сеток.
- (рисунок в центре).
Сетка из проволоки клиновидного профиля
- (рисунок слева).
- Рейтинг фильтрации более 50-100 мкм (как правило — более 200 мкм).
- Применение щеточной технологии очистки.
Стоимость различных сеток примерно одинакова. Исключение — плетеные сетки тонких и очень тонких рейтингов фильтрации (10-50 мкм)
Сетка из проволоки клиновидного профиля оптимальна при щеточной очистке в условиях возможного появления в фильтруемой жидкости тяжелых нефтепродуктов — щетки движутся вдоль щелей, образованных проволокой и удаляют возможные налипания.
ИСПОЛНЕНИЕ КОРПУСА И СПОСОБ ПОДКЛЮЧЕНИЯ К ТРУБОПРОВОДАМ
Самый дешевый вариант конструкции фильтра. Фильтруемая жидкость подается непосредственно в цилиндр фильтрующей сетки. Возможно два варианта подключения к трубопроводам.
- Вертикальная установка
достоинства:- Минимальная требуемая производственная площадь.
- Простота организации байпасса.
недостатки:
- Сложность профилактической разборки, т.к. технологическая зона разборки располагается сверху.
- Не самые комфортные условия для работы щеточного механизма очистки сетки.
- Горизонтальная установка
достоинства:- Простота профилактической разборки, направление технологической зоны разборки позволяет разобрать и собрать фильтр без применения подьемных механизмов, лестниц и т.п.
- Комфортные условия для работы щеточного механизма очистки сетки.
- Простота организации байпасса.
недостатки:
- Большая занимаемая производственная площадь.
Чуть более дорогой вариант конструкции фильтра. Фильтруемая жидкость подается непосредственно в цилиндр фильтрующей сетки.
достоинства
- Минимальная требуемая производственная площадь.
- Простота разборки-сборки при проведении профилактических работ.
- :
недостатки
- :
- Сложность организации байпасса.
Более дорогой вариант конструкции фильтра. Фильтруемая жидкость подается сначала на сетку грубой очистки, а уже затем в цилиндр основной фильтрующей сетки.
достоинства
- Существенно более высокая надежность работы при применении двух фильтрующих сеток (см. ниже).
- Простота организации байпасса.
- Простота разборки-сборки при проведении профилактических работ.
- :
недостатки
- :
- Увеличение площади, занимаемой фильтром.
ВСТРОЕННЫЙ ГРЯЗЕВИК
В промышленных условиях (прежде всего при фильтрации жидкостей оборотных циклов и водозаборов из открытых источников) возможно попадание в контур очистки крупных предметов — камней и, не редкий вариант, пленок, ткани, веревок…
Пленки и ткани (полиэтилен, линолиум), а также крупные камни, веревки, провода… не могут быть удалены из корпуса фильтра с помощью сканерной или щеточной технологий. Эти предметы попросту не проходят через сбросной клапан.
Извлечение таких загрязнений требует разборки фильтра квалифицированным персоналом. Этот процесс занимает значительное время.
Применение параллельного расположения подающего и отбирающего портов позволяет применить в фильтре сетку предварительной очистки («грязевик») для задержки крупных предметов.
Жидкость подается во входной порт (1), затем проходит через сетку (2) грубой очистки (отверстия 5-10 мм) снаружи-внутрь. Таким образом, крупные предметы задерживаются на внешней стороне грубой сетки в камере (6) — расстояние между внешней поверхностью сетки и внутренней поверхностью корпуса — несколько сантиметров.
После предварительной фильтрации жидкость поступает внутрь цилиндра основной сетки (3). Основная фильтрация осуществляется изнутри-наружу с последующим отбором через порт (5).
Задержанные крупные предметы могут быть удалены после снятия крышки (4) (зеленые стрелки). Этот процесс не требует заметного времени и высокой квалификации персонала и не влечет разборку механизма очистки фильтра.
РАБОТА НЕСКОЛЬКИХ ФИЛЬТРОВ НА ОБЩИХ ТРУБОПРОВОДАХ
При необходимости увеличения производительности фильтрующей системы возможно применение нескольких параллельно расположенных фильтров. Причем фильтры могут управляться одним пультом управления, что обеспечивает последовательную синхронизацию промывок и снижает стоимость системы.
Оптимальным вариантом установки нескольких фильтров является подключение их к параллельным трубопроводам — подающему, отбирающему и трубопроводу для отбора шлама.
Пример такой установки показан на эскизах для L-образного корпуса и корпуса с односторонним расположением портов.
НЕСКОЛЬКО ФИЛЬТРОВ С ОДНОЙ СЕТКОЙ ИЛИ ОДИН ФИЛЬТР С НЕСКОЛЬКИМИ СЕТКАМИ?
Другим способом увеличения производительности фильтрующей системы является применение многосеточных фильтров (MEGA и TWIN)
Стоимость четырех параллельно работающих фильтров и фильтра с четырьмя сетками — примерно одинакова.
Фильтры типа «MEGA» более сложны в обслуживании, но занимают значительно меньше места по площади пола (по высоте — больше).
Применение того или иного решение в этой части — дело технической целесообразности и правильного учета условий эксплуатации, но не экономических соображений.
Комплекс автоматизированного проектирования и производства микроволновых фильтров
Автоматизированный координатограф «Скальпель-07»
Комплекс предназначен для автоматизированного проектирования и производства полосно-пропускающих фильтров полосковых и микрополосковых конструкций в диапазоне частот от 20 МГц до 20 ГГц с относительной шириной полосы пропускания 1—100 %.
Комплекс включает в себя
- Экспертную систему Filtex32 для проектирования и исследования фильтров
- Автоматизированный координатограф «Скальпель-96» для изготовления фильтров
Экспертная система Filtex32 представляет собой программный продукт, зарегистрированный в Реестре программ для ЭВМ (№ 2008612877, RU ОБПБТ №3(64) 20.09.2008). Экспертная система Filtex32 работает под управлением 32-разрядной операционной системы Windows 2000/XP/Vista. Система Filtex32 состоит из управляющей оболочки и банка конструкций фильтров, оформленных в виде динамически подключаемых библиотек.
Управляющая оболочка позволяет выбрать конструкцию фильтра, задать её параметры, отобразить топологию полосковых проводников и отвечающие им частотные характеристики, ввести техническое задание на разовый синтез конструкции или на серийный синтез со сканированием по одному из параметров.
Банк конструкций фильтров постоянно пополняется dll-библиотеками новых конструкций. Конструкции отображаются в виде иерархического дерева. В каждом узле дерева содержатся конструкции, сгруппированные по типу резонаторов их образующих, и отличающиеся количеством звеньев. На текущий момент насчитывается 23 узла, содержащих 109 конструкций.
Динамически подключаемая библиотека конструкции содержит описание конструкции фильтра, список конструктивных параметров, пример настроенного фильтра, подпрограмму расчёта частотных характеристик, подпрограмму интеллектуальной оптимизации конструкции.
Главное окно управляющей оболочки экспертной системы Filtex32
Расчёт частотных характеристик выполняется в рамках одномерной модели, содержащей отрезки одиночных и связанных линий передачи. В явном виде рассматриваются только волны основного типа, влияние волн высших типов моделируется введение эффективных ёмкостей. Дисперсия учитывается в рамках приближенной модели.
В основе интеллектуальной оптимизации фильтра лежит использование универсальных априорных и специфических апостериорных знаний о синтезируемой конструкции.
Примеры конструкций фильтров
Автоматизированный координатограф «Скальпель-07» работает под управлением компьютера и позволяет полностью заменить фотолитографию при изготовлении микрополосковых структур во всех случаях, когда не требуется слишком высокого разрешения. Тонкое микролезвие аппарата, прорезает слой эластичного лака, которым предварительно покрыта металлизированная подложка. С удаляемых участков металлизации лак снимает-ся под микроскопом, а затем проводится обычное химическое травление структуры, аналогичное стандартной технологии фотолитографии.
Работа прибора основана на использовании четырёх шаговых приводов, два из которых перемещают столик с закрёпленным на нём держателем подложки по координатам X и Y. Третий привод осуществляет поворот резака вокруг своей оси так, чтобы его лезвие всегда было ориентировано вдоль направления реза. Четвёртый привод поднимает и опускает предметный столик на заданную величину на изломах линий рисунка проводников, чтобы исключить контакт подложки с резаком во время поворота лезвия.
Комплекс отличается простотой и лёгкостью обращения с ним и не предусматривает предварительного обучения персонала.
Изготовленные фильтры
Комплекс успешно эксплуатируется в течение многих лет в ряде конструкторских бюро промышленных предприятий России и в научно-исследовательских лабораториях университетов.
Напорный фильтр — Энциклопедия по машиностроению XXL
Расчет напорных фильтрующих насыпей (рис. XI. 17). Расчет заключается в определении размеров поперечного сечения сооружения в зависимости от допускаемого напора перед сооружением. Форма поперечного сечения сооружений может быть различна. На рис. XI. 18 показана насыпь треугольного сечения, а на рис. XI.19 — трапецоидального сечения с меньшим основанием, обращенным книзу.
[c.287]
Рекомендуемая последовательность расчета напорных фильтрующих насыпей приводится в задаче (XI.22). [c.289]
Для определения допускаемых напоров в данном случае используются те же уклонные коэффициенты, что и для напорных фильтрующих насыпей.
[c.289]
XI.23. Напорная фильтрующая насыпь, выполненная из камня элювиального происхождения неправильной, остроугольной формы, со средним диаметром, приведенным к шару, d = 30 см, должна пропустить расход Q = 3 м /с. Длина фильтрующей насыпи S = 19 м уклон дна русла I o = 0,02. Рассчитать размеры сечения фильтрующей насыпи прямоугольного сечения реки, если а) высота бровки земляного полотна Ян = 3 м грунт основания мелкий песок б) На = 2,5 м грунт основания суглинок. [c.291]
Напорным фильтрам присущи все основные конструктивные элементы, которые имеют место в открытых фильтрах. В качестве распределительной системы наиболее часто применяют щелевую трубчатую или колпачковую. Это позволяет отказаться от устройства поддерживающих слоев. [c.253]
Обрабатываемая вода поступает на фильтр под давлением, которое обеспечивает преодоление сопротивлений в фильтре и подачу фильтрата непосредственно в сеть потребителя, минуя второй подъем. При достижении потери напора в фильтре порядка 10 м он выключается на промывку. Промывку напорных фильтров рационально производить с воздухом. Для подачи воздуха обычно предусматривают отдельную систему. [c.253]
В схемах технического водоснабжения при мутности исходной воды до 150 мг/л часто напорные фильтры являются единственными очистными сооружениями. [c.253]
Для осветления производственной воды Г. Н. Никифоровым были предложены и внедрены сверхскоростные напорные фильтры, работающие со скоростью фильтрования до 100 м/ч. Объем фильтра вертикальными перегородками разделен на восемь камер, поочередно автоматически промывающимися, т. е. в каждый момент работы фильтра семь камер фильтруют воду, а одна промывается, на что используется часть фильтрата остальных камер. [c.253]
Запахи и привкусы, обусловленные наличием в воде микроорганизмов, могут быть устранены также фильтрованием воды через слой активного гранулированного угля в напорных фильтрах или введением порошкообразного угля в воду перед фильтрованием на открытых песчаных фильтрах. При больших дозах (более 5 мг/л) уголь следует вводить на насосной станции I подъема или одновременно с коагулянтом в смеситель, но не ранее чем через 10 мин после введения хлора. Рекомендуется дозировать активный уголь в виде пульпы концентрацией 5. .. 10%. При дозах угля до 1 мг/л допускается сухое дозирование угольного порошка (по массе и по объему). Особенно целесообразно приме- [c.255]
При величине рН>6,7 и содержании железа в воде до 5 мг/л обезжелезивание можно производить без градирен с обогащением воды воздухом путем излива ее с высоты 0,5 м в карман открытого фильтра или путем введения воздуха в трубопровод перед напорными фильтрами. [c.266]
Устанавливают фильтры на сливной линии перед гидробаком, а подпиточные и напорные фильтры после насоса подпитки или основного насоса. Их располагают в
[c.251]
Напорный фильтр 386 Напряжение прикосновения 434, 435, 440
[c.494]
Большое значение приобрела очистка промывных вод гальванических производств методами ионного обмена [15]. Перед ионообменными фильтрами ставят механический напорный фильтр для защиты ионообменных фильтров от механических загрязнений. Сточную воду после механических фильтров подают на сильнокислый катионит в Н-форме, на котором удаляются имеющиеся в воде катиониты. Фильтрат после катионитного фильтра содержит кислоты, соответствующие содержащимся в стоках анионам, его pH равен 2,7—3,7. Фильтрат подают далее на слабоосновный анионит в ОН-форме, где происходит удаление анионов. Кроме того, анионитный фильтр задерживает часть поверхностно-активных веществ. Вода, полученная таким образом, повторно используется в производственных процессах. [c.139]
На фиг. 1 показана конструкция зернистого напорного фильтра, применяемого на водоочистительных установках. [c.196]
| Фиг. 1. Зернистый напорный фильтр. |
Коагуляция в напорных фильтрах при одно- Меньше 10 3,5
[c.312]
Нормальная производительность механических напорных фильтров может приближенно оцениваться по поминальной скорости фильтрования, определяемой, исходя из характера предварительной химической обработки воды, качества фильтруемой воды и конструктивных особенностей фильтров соответственно материалам табл. 14-2. [c.313]
Корпус напорного фильтра представляет собой стальной сварной цилиндр с приваренными к нему сферическими днищами. По условиям транспортабельности в собранном виде по железным дорогам максимальный диаметр изготовляемых заводами напорных фильтров равен 3,4 м. Горизонтальные фильтры изготовляют диаметром 3,0 с длиной корпуса 5,5 и 10,0 м. Фильтры диаметром 1,0 м и меньше изготовляют иногда с разъемным верхним днищем на фланцах, а фильтры диаметром меньше 0,5 м — с плоскими сварными или разъемными днищами. Напорные фильтры рассчитывают обычно на рабочее давление до 0,6 Мн/м .
[c.264]
Опыт эксплуатации фильтров с поддерживающими слоями выявил их основной недостаток — возможность смещения и перемешивания слоев в результате резкого изменения по различным причинам расхода воды в отдельных местах поперечного сечения фильтра, приводящего к аварийному выходу фильтра из работы вследствие, во-первых, возможности проникновения основной зернистой загрузки в трубопровод обработанной воды и, во-вторых, проскока из фильтра воды ухудшенного качества. Это обстоятельство, а также стремление снизить высотные габариты фильтров и тем самым уменьшить удельные расходы металла на их изготовление привели за последнее десятилетие к преимущественному применению у нас в напорных фильтрах распределительных устройств без поддерживающих слоев с непосредственной загрузкой на эти устройства фильтрующего материала. [c.266]
Такие устройства в напорных фильтрах электростанций были впервые применены в СССР М. И. Чиркиным, предложившим конструкцию пористого колпачка, изготовление которого было затем- освоено на Московском абразивном заводе (рис. 8-2). Пористая масса для колпачка приготовляется путем склеивания кварцевой крошки размером около 2,0 мм бакелитовым лаком и последую- 1-щей сушки ее при температуре до 150° С. В нижней части колпачка помещена пластмассовая гайка с трубной резьбой /а» для навертывания его на штуцера распределительного устройства, выполняемого в виде трубчатой системы или ложного днища (рис. 8-3).
[c.267]
Верхние распределительные устройства напорных фильтров находятся в более благоприятных условиях, чем нижние, поскольку их всегда отделяет от зернистой загрузки водяная подушка, создающая горизонтальную ком- [c.276]
Ниже представлены схематически наиболее распространенные конструкции верхних распределительных устройств в напорных фильтрах. [c.278]
ВОДГЕО на основе изучения идеи такого фильтра предложил и разработал схему применения ее для группы стандартных напорных механических фильтров, обслуживаемых одним промывным баком. Схема такого фильтра показана на рис. 8-44. Осветляемая вода, пройдя распределитель и воздухоотделитель 2, поступает по трубопроводу 3 через гидравлический затвор 4 и трубопровод 5 в напорный фильтр 1. Фильтрат по трубопроводам 6 к 12 поступает сначала в промывной бак 8, после наполнения которого вода через сборный лоток 7 и трубопровод 13 направляется в бак осветленной воды. Далее, так же как у описанного выше фильтра, происходит постепенное заполнение сифона 9, свободный конец которого снабжен плавающим клапаном И, открывающимся по достижении высоты столба воды над ним 2 м, после чего начинается промывка фильтра. Прекращение промывки происходит после опорожнения бака 8 и разрыва сифона 9 трубкой 10. По подсчетам ВОДГЕО для группы из пяти механических фильтров диаметром 3,0 м требуется промывной бак емкостью 15 м , а производительность установки при скорости фильтрования 6 м.1ч составит 210 м 1ч. При этом для промывки каждого фильтра частично используется фильтрат всех остальных работающих фильтров. [c.287]
В случае применения напорных фильтров (одно- или двухпоточных) ф окончательно определяется после подбора количества и диаметра фильтров стандартных размеров (табл. 11-10), причем скорость фильтрования ос.ф в должна превышать указанных величин как при работе всех фильтров, так и при промывке одного из них.
[c.527]
Трубчатый отстойник и напорный фильтр заводского изготовления (типа Струя ) До 1000 1 До 1,5 До 120 До 20 До 1600 [c.56]
За рубежом для глубокого осветления воды широко используют механические напорные фильтры циклонные, вращающиеся со съемными фильтровальными элементами из фарфора или стали (размер отверстий 0,1. .. 1,6 мм), и автоматические фильтры с множеством фильтровальных трубок с отверстиями 125 мкм и более и вращающимися промывным устройством. [c.150]
Площадь поперечного сечения напорной фильтрующей пасыпи определяется по зависимости [c.288]
XI.24. Напорная фильтрующая насыпь трапецеидального сечения с меньшим основанием, обращенным книзу, выполненная из камня гляциального происхождения средней окатанности диаметром d == = 35 см, должна пропустить расход Q = 2,7 м /с. Высота бровки земляного полотна Ян = 2,5 м. Коэффициент заложения откосов фильтрующей насыпи/Иф = 1,5. Уклон лога I o = 0,05. Рассчитать размеры поперечного сечения фильтрующей насыпи, если а) длина фильтрующей насыпи 5 = 20 м грунт основания суглинок б) 5 = 27 м грунт основания илистый. [c.292]
Катионитовые фильтры могут быть напорные и открытые. Наиболее распространены напорные катионитовые фильтры, главным образом вертикальные. Конструкция их не отличается существенно от обычных скорых песчаных напорных фильтров. В нижней части фильтра расположена дренажная система с щелевыми дренажными колпачками для отвода умягченной воды с распределения воды при взрыхлении катионита. Умягчаемая и отмывочная вода подаются через расположенную вверху воронку, способствующую равномерному распределению воды по площади фильтра. Через нее же отводится из фильтра вода при взрыхлении катионита. В верхней части фильтра расположено трубчатое устройство для распределения по площади фильтра регенерирущего раствора. Металлический корпус Н-катионитового фильтра, трубопроводы и арматура должны быть защищены противокоррозионным покрытием, стойким в кислой среде. Дренажное и распределительное устройства в этих фильтрах должны быть выполнены из кислотостойкого материала. [c.263]
При режиме водообмена вода из ванны 10 через донные выпуски 13 поступает на грубые фильтры 12. После предварительной очистки от грубодисперсных загрязнений водд циркуляционными насосами 3 подается для глубокого осветления на напорные фильтры 16, которые промывают чистой водой с помощью насосов 21. Очищенная и подогретая в скорых водонагревателях 14 вода вновь поступает в ванну через циркуляционные впуски И. Циркуляционный расход и количество воды для промывки фильтров измеряются расходомерами 15 и 19. Верхний слой воды из ванны отводится через трапы переливных лотков 9 во всасывающую линию циркуляционного контура. При необходимости вода из переливных лотков может быть направлена на сброс в лоток 20 водостока или канализацию. [c.397]
Особенность фильтрования биологически очищенных бытовых сточных вод, доочищенных коагуляцией, заключается в отсутствии взвешенных частиц активного ила, образующих прочные агрегаты на поверхности зерен и вызывающих скольжение осадка в начальных слоях. Свойства поступающей на фильтр взвеси и характер процесса фильтрования при этом аналогичны очистке природных вод. Рост потери напора носит практически линейный характер. Поэтому для фильтрования коагулированных бытовых сточных вод рекомендованы стандартные напорные фильтры с подачей воды сверху вниз. Фильтрование осуществляется через двухслойную загрузку. Нижний слой — песок 400—500 мм, верхний—антрацит 600—700 мм. В качестве подстилочного слоя применяется гравий 200—300 мм. Для повышения эффекта очистки всей толщи загрузки применяется водовоздушная отмывка механически очищенной водой с подачей отработавшей воды на вход отстойника.
[c.246]
Наличие отстойного резервуара в конструкции экономайзера можно рассматривать лишь как первую ступень очистки воды. В случае установки экономайзера с промежуточным теплообменником более глубокая очистка не требуется. К тому же она резко снизила бы эффективность работы экономайзера. При прямом использовании нагретой в экономайзерах воды в качестве второй ступени очистки воды может устанавливаться специальный ос-ветлительный напорный фильтр, покрытый тепловой изоляцией во избежание чрезмерных потерь тепла. [c.209]
Коагуляция в напорных фильтрах при двухсту- Меньше 5 [c.312]
В ВОДГЕО была предложена аналогичная схема для группы безарматурных напорных механических фильтров, обслуживаемых оДним промывным баком. Для одного такого фильтра показана схема на рис. 8.7. Осветляемая вода, пройдя распределитель и воздухоотделитель 2, поступает по трубопроводу 3 через гидравлический затвор 4 и трубопровод 5 в напорный фильтр 1. Фильтрат по трубопроводам б и 12 поступает сначала в промывной бак 8, после заполнения которого вода через сборный лоток 7 и трубопровод 13 направляется в бак осветленной воды. Далее, так же как у описанного выше фильтра, происходит постепенное заполнение сифона 9, свободный конец которого снабжен плавающим клапаном 11, открывающимся по достижении высоты столба воды над ним 2 м, после чего начинается промывка фильтра. Прекращение промывки происходит после опорожнения бака 8 и разрыва сифона 9 трубкой 10. [c.148]
Фильтрование воды в механическом фильтре происходит за счет разности давлений над и иод фильтрующим слоем. Эта разность давлений называется потерей наиора в фильтре. Сопротивление (потеря наиора) в фильтрующем слое тем больше, чем выше скорость фильтрования, высота фильтрующего слоя, степень его загрязнения и чем меньше размер зерен фильтрующего материала. Фильтрование воды сопровождается увеличением гидравлического сопротивления фильтра вследствие накоиления в фильтрующем слое задержанной взвеси и уменьшения свободного объема пор между зернами фильтрующего материала. Сопротивление чистого фильтрующего слоя механического напорного фильтра равно 4 кПа, а максимально допустимое соиротивление — 0,1 МПа. [c.21]
| Рис. 2-6. Установка напорного фильтра для определения взвешенного и pa TBopeniioro железа. |
I — конденсатопровод 2 — зонд З— кран пробковый 4 — холодильник прямотрубный вертикальный 5 — напорный фильтр для взвешенных окислов. келеза 6 — Н-катионнто-вый фильтр для задержания растворенного железа и других катионов 7 — мерный бачок.
[c.31]
В большинстве случаев обработка воды для однотрубного транспорта тепла может производиться по простейшим схемам без подогрева воды до высокой тем,пе ратуры. Это особенно важнэ, так как хорошо увязывается со схемой подогрева воды паром из отборов и решает вопрос о защите сетевых подогревателей от загрязнений. Одной из таких схем является схема коагуляции воды в напорных фильтрах с последующим Н-катионированием с голодной регенерацией. Такие схемы осуществимы в настоящее время для крупных установок, так как единичная производительность аппаратов напорного типа достигает 300 м 1ч. Для электростанций большей мощности, которые рассчитаны на отдачу 1 ООО Гкал1ч и больше, необходимо стремиться к увеличению производительности аппаратов, так как число их уже исчисляется десятками. [c.102]
При работе фильтронасосной установки любого типа в качестве фильтрующего элемента можно применять те же тканевые мешки, помещая их в ванне, или, для экономии рабочей площади ванны, — в лотки из резины, расположенные за бортом ванны, на верхней плоскости бортового отсоса. Употребляются и напорные фильтры, которые выполняются в виде коробки-корпуса, заполненного фильтрующим элементом, с входным и выходным отверстиями, к которым присоединяют входной и выходной шланги. В качестве фильтрующих элементов употребляют стеклоткань, стекловату (которые предварительно кипятят) и ткани. Корпус напорного фильтра [c.101]
Конструкция ВЧ-фильтра »Примечания по электронике
При проектировании ВЧ-фильтра
используются некоторые ключевые методики, позволяющие производить расчеты наиболее эффективным способом.
RF Filters Включает:
RF Filters — основы
Характеристики фильтра
Основы проектирования ВЧ-фильтров
Конструкция фильтра высоких и низких частот
Постоянный k-фильтр
Фильтр Баттерворта
Чебычевский фильтр
Фильтр Бесселя
Эллиптический фильтр
Кристаллический фильтр
Дизайн ВЧ-фильтра часто считается сложной задачей и предназначен только для специалистов-разработчиков.Хотя конструкция ВЧ-фильтра может быть сложной, процесс можно упростить и раскрыть, чтобы его мог выполнить разработчик электроники.
Чтобы обеспечить оптимальную конструкцию ВЧ-фильтра, необходимо иметь необходимые требования к параметрам рабочих характеристик, чтобы можно было принимать решения о топологии, типах фильтров и т.п.
Однако, какой бы ни была фактическая конструкция фильтра, для разработки любого фильтра используется одна и та же базовая методика.Использование методологии означает, что учитываются все необходимые требования, используется правильный подход к проектированию и, в конечном итоге, создается правильный ВЧ-фильтр.
Основы проектирования ВЧ-фильтров
В общем, фильтры изменяют амплитуды и фазы синусоидальных сигналов, которые проходят через них. Это изменение зависит от частоты отдельных синусоид в общей форме волны.
Большинство фильтров называют линейными фильтрами. Как таковые, у них нет нелинейных действий, в которых ответ пропорционален входному сигналу.Вместо этого сигналы проходят, и их амплитуда и фаза изменяются линейным образом в соответствии с их частотой.
Из этого можно определить некоторые из ключевых параметров конструкции RF-фильтра, которые являются факторами, на которые изменяется сигнал, а именно усиление G и фазовый сдвиг θ. Поскольку и коэффициент усиления G, и фазовый сдвиг θ зависят от частоты, т.е. они являются функциями частоты, их можно выразить следующим образом:
Эти две функции представляют характеристику амплитуды (часто называемую частотной характеристикой) и фазовую характеристику фильтра соответственно.
Эти две функции управляют основными функциями, которые необходимо знать о фильтре. Имея возможность определять функции, можно разработать ВЧ-фильтр.
Обычно в первом случае используется пример конструкции ВЧ-фильтра нижних частот, а затем он расширяется за счет включения других форм фильтра. Соответственно, сначала мы рассмотрим конструкцию фильтра нижних частот.
Настоящие и идеальные фильтры
При разработке ВЧ-фильтра было бы идеально, если бы фильтр пропускал сигналы в полосе пропускания без каких-либо изменений амплитуды или фазы.Такие фильтры могут иметь прямоугольную характеристику, переходящую прямо в полосу задерживания и обеспечивающую требуемый уровень затухания полосы задерживания.
К сожалению, невозможно разработать подобные ВЧ-фильтры, а реальные конструкции ВЧ-фильтров могут только приблизиться к идеальным кривым и параметрам отклика. Затем эти приближения можно использовать в качестве различных существующих фильтров. К ним относятся Баттерворт, Бессель, Чебышев, Эллиптический, Гауссовский и многие другие.
Используя математический подход к разработке РЧ-фильтра, можно использовать математическое соотношение.Можно доказать, что квадрат отклика для всех реализуемых фильтров можно выразить как отношение двух четных, то есть рациональных полиномов. Это означает, что общее математическое выражение для всех конструкций RF-фильтров:
Разработка и нормализация ВЧ-фильтра
Хотя для фильтров Баттерворта и фильтров с постоянным K доступны относительно простые уравнения, другие формы фильтров требуют более сложных вычислений.
Подход к разработке RF-фильтров, который использовался в течение многих лет, использует так называемые нормализованные фильтры.Набор переменных рассчитывается для стандартного набора условий, и они помещаются в таблицу, готовые к использованию и масштабированию до требуемых условий.
Нормализованный фильтр должен иметь частоту среза 1 радиан в секунду, то есть 0,159 Гц, и импеданс 1 Ом. Затем эти значения можно очень легко масштабировать для использования при требуемой частоте и сопротивлении. Таким образом, утомительная и сложная математика, необходимая для проектирования ВЧ-фильтра, была сведена лишь к определению требований и последующему нахождению соответствующей таблицы значений.Таблицы доступны в различных книгах и даже в Интернете.
Требования, которые необходимо выбрать в первую очередь, включают такие параметры, как тип фильтра (Баттерворт, Чебышев и т. Д.), Уровень пульсации и т. Д., Порядок фильтров (т. Е. Количество катушек индуктивности и конденсаторов) и т. Д.
После их выбора можно найти соответствующую таблицу и определить значения элементов в фильтре.
Разработка и масштабирование ВЧ-фильтра
После того, как конструкция фильтра реализована в его нормализованной форме, необходимо преобразовать значения в требуемые частоту и импеданс.В нормализованном формате конструкция фильтра имеет отсечку 0,159 Гц, то есть 1 радиан в секунду, и он рассчитан на работу при сопротивлении нагрузки 1 Ом.
С = Cn2πfcR
L = R Ln2 π fc
Где:
C = действительное значение конденсатора
L = действительное значение индуктора
Cn = нормализованное значение конденсатора
Ln = нормализованное значение индуктора
R = требуемое значение резистора нагрузки
fc = требуемая частота отсечки
Процесс разработки RF-фильтра
Процесс разработки ВЧ-фильтра состоит из нескольких этапов.Следование этому порядку помогает логически спроектировать РЧ-фильтр. Эти шаги относятся к конструкции фильтра нижних частот — дальнейшие этапы перехода на фильтр верхних частот или полосовой фильтр приведены на следующих страницах.
Хотя некоторые компьютерные программы могут допускать прямое проектирование, часто проектирование с использованием таблиц и т. Д. Все еще широко используется. Если используется компьютерная программа, процесс проектирования фильтра может быть соответствующим образом изменен.
- Определите необходимый ответ: Первым этапом процесса является фактическое определение требуемого ответа.Такие элементы, как точка отсечки, затухание в заданной точке и т. Д.
- Нормализовать частоты: Чтобы иметь возможность использовать различные таблицы и диаграммы кривых фильтров, необходимо преобразовать все частоты так, чтобы точка отсечки находилась на уровне 1 радио в секунду, а любые другие точки были относительными. к этому.
- Определите максимальную пульсацию в полосе пропускания: Один из основных шагов при разработке РЧ-фильтра — понять, насколько допустима внутриполосная пульсация.Чем больше пульсация, тем больший уровень селективности можно получить. Чем выше избирательность, тем быстрее будет переход от полосы пропускания к окончательному спаду.
- Сопоставьте требуемые кривые затухания с кривыми из фильтра: Зная характеристики, как пульсации, так и подавления, необходимые в определенных точках, можно определить тип фильтра, а также порядок или количество требуемых элементов. в конструкции фильтра.
- Определить значения элементов: Используя соответствующие справочные таблицы, можно определить нормализованные значения компонентов фильтра.
- Масштаб нормализованных значений: Наконец, значения необходимо масштабировать для требуемой частоты среза и сопротивления.
Значения фильтров и кривые можно найти в ряде книг по проектированию фильтров, включая «Handbook of Filter Synthesis» от Zvrev, pub Wiley.
Сегодня многие программы или приложения для проектирования схем и фильтров доступны в режиме онлайн или в виде приложения для загрузки.
С помощью этих приложений часто можно напрямую ввести требования и отобразить дизайн. Тем не менее, все же желательно уметь понимать процесс проектирования, исходя из основных принципов, и таким образом можно лучше понять ограничения компромиссов.
Понимание основ проектирования ВЧ-фильтров не только позволяет проектировать фильтры, но даже если фактический дизайн не разрабатывается, это дает более полное представление о процессе и технических характеристиках самих фильтров.
Другие важные темы по радио:
Радиосигналы
Типы и методы модуляции
Амплитудная модуляция
Модуляция частоты
OFDM
ВЧ микширование
Петли фазовой автоподстройки частоты
Синтезаторы частот
Пассивная интермодуляция
ВЧ аттенюаторы
RF фильтры
Радиочастотный циркулятор
Типы радиоприемников
Радио Superhet
Избирательность приемника
Чувствительность приемника
Обработка сильного сигнала приемника
Динамический диапазон приемника
Вернуться в меню тем радио.. .
Введение в конструктор фильтров
— Пример MATLAB и Simulink
Этот пример показывает, как использовать Filter Designer в качестве удобной альтернативы функциям проектирования фильтров командной строки.
Filter Designer — это мощный графический пользовательский интерфейс (GUI) в Signal Processing Toolbox ™ для разработки и анализа фильтров.
Filter Designer позволяет быстро проектировать цифровые фильтры FIR или IIR, устанавливая спецификации производительности фильтров, импортируя фильтры из рабочего пространства MATLAB® или добавляя, перемещая или удаляя полюса и нули.Filter Designer также предоставляет инструменты для анализа фильтров, такие как графики амплитуды и фазовой характеристики и графики полюс-ноль.
Приступая к работе
Введите filterDesigner в командной строке MATLAB:
>> filterDesigner
Отображается диалоговое окно Совет дня с предложениями по использованию Filter Designer. Затем отображается графический интерфейс с фильтром по умолчанию.
Графический интерфейс состоит из трех основных областей:
В верхней половине графического интерфейса отображается информация о спецификациях фильтра и ответах на текущий фильтр.В области «Текущая информация о фильтре» в верхнем левом углу отображаются свойства фильтра, а именно структура фильтра, порядок, количество используемых разделов и стабильность фильтра. Он также предоставляет доступ к диспетчеру фильтров для работы с несколькими фильтрами.
В области отображения фильтра в правом верхнем углу отображаются различные отклики фильтра, такие как отклик величины, групповая задержка и коэффициенты фильтра.
Нижняя половина графического интерфейса пользователя — это интерактивная часть Filter Designer.Панель дизайна в нижней половине — это то место, где вы определяете свои характеристики фильтра. Он контролирует то, что отображается в двух других верхних областях. Другие панели можно отобразить в нижней половине с помощью кнопок боковой панели.
Инструмент включает контекстную справку. Вы можете щелкнуть правой кнопкой мыши или выбрать Что это? Кнопка для получения информации о различных частях инструмента.
Разработка фильтра
Мы разработаем фильтр нижних частот, который пропускает все частоты, меньшие или равные 20% частоты Найквиста (половина частоты дискретизации), и ослабляет частоты, превышающие или равные 50% частоты Найквиста.Мы будем использовать FIR Equiripple фильтр со следующими характеристиками:
Затухание полосы пропускания 1 дБ
Затухание полосы задерживания 80 дБ
Частота полосы пропускания 0,2 [Нормализовано (от 0 до 1)]
Частота полосы задерживания 0,5 [Нормализованный (от 0 до 1)]
Для реализации этой схемы мы будем использовать следующие спецификации:
1. Выберите Lowpass из раскрывающегося меню под Response Type и Equiripple в FIR Design Метод .Как правило, при изменении типа отклика или метода разработки параметры фильтра и область отображения фильтра обновляются автоматически.
2. Выберите Укажите порядок в области Порядок фильтра и введите 30 .
3. КИХ-фильтр Equiripple имеет параметр Density Factor , который управляет плотностью частотной сетки. При увеличении значения создается фильтр, который более точно приближается к идеальному равнопроходному фильтру, но по мере увеличения вычислений требуется больше времени.Оставьте это значение на 20.
4. Выберите Нормализованный (от 0 до 1) в раскрывающемся меню Единицы в области Спецификации частоты .
5. Введите 0,2 для wpass и 0,5 для wstop в области Frequency Specification .
6. Wpass и Wstop в области Magnitude Specification — положительные веса, по одному на полосу, используемые во время оптимизации в FIR Equiripple фильтре.Оставьте эти значения равными 1.
7. После установки проектных спецификаций нажмите кнопку Design Filter в нижней части графического интерфейса, чтобы разработать фильтр.
Отклик величины фильтра отображается в области анализа фильтра после вычисления коэффициентов.
Просмотр других анализов
После того, как вы создали фильтр, вы можете просмотреть следующие анализы фильтра в окне дисплея, нажав любую из кнопок на панели инструментов:
В порядке слева направо кнопки
Изменение Единицы измерения осей
Вы можете изменить единицы измерения оси x или y, щелкнув правой кнопкой мыши на метке оси и выбрав нужные единицы.Текущие единицы отмечены галочкой.
Маркировка точек данных
В области отображения вы можете щелкнуть любую точку на графике, чтобы добавить маркер данных, который отображает значения в этой точке. Щелчок правой кнопкой мыши по маркеру данных отображает меню, в котором вы можете перемещать, удалять или настраивать внешний вид маркеров данных.
Оптимизация дизайна
Чтобы минимизировать стоимость реализации фильтра, мы попытаемся уменьшить количество коэффициентов, используя опцию Minimum Order в панели дизайна.
Измените выбор в Filter Order на Minimum Order в области дизайна и оставьте остальные параметры без изменений.
Нажмите кнопку Design Filter , чтобы создать новый фильтр.
Как вы можете видеть в области информации о текущем фильтре, порядок фильтров уменьшился с 30 до 16, количество волн уменьшилось, а ширина перехода стала шире. Характеристики полосы пропускания и полосы задерживания по-прежнему соответствуют критериям проектирования.
Изменение параметров анализа
Щелкнув правой кнопкой мыши график и выбрав Параметры анализа, можно отобразить диалоговое окно для изменения параметров анализа. (Вы также можете выбрать «Параметры анализа» в меню «Анализ».)
Чтобы сохранить отображаемые параметры в качестве значений по умолчанию, щелкните Сохранить как значение по умолчанию . Чтобы восстановить значения по умолчанию, определенные MATLAB, нажмите Restore Original Defaults .
Экспорт фильтра
Как только вы будете удовлетворены своим дизайном, вы можете экспортировать свой фильтр в следующие места назначения:
Рабочее пространство MATLAB
MAT-файл
Текстовый файл
Выбрать Экспорт из меню Файл .
Когда вы выбираете экспорт в рабочее пространство MATLAB или в MAT-файл, вы можете экспортировать фильтр как коэффициенты. Если доступен DSP System Toolbox ™, вы также можете экспортировать свой фильтр как системный объект.
Создание файла MATLAB
Filter Designer позволяет вам сгенерировать код MATLAB для воссоздания вашего фильтра. Это позволяет вам встроить ваш дизайн в существующий код или автоматизировать создание ваших фильтров в скрипте.
Выберите Generate MATLAB code из меню File , выберите Filter Design Function и укажите имя файла в диалоговом окне Generate MATLAB code.
Следующий код был сгенерирован из фильтра минимального порядка, который мы разработали выше:
Квантование фильтра
Если у вас установлен DSP System Toolbox ™, панель Установить параметры квантования доступна на боковой панели:
Вы можете используйте эту панель для квантования и анализа фильтров двойной точности. С помощью DSP System Toolbox вы можете выполнять квантование от двойной точности до одинарной точности. Если у вас есть Fixed-Point Designer, вы можете квантовать фильтры с точностью до фиксированной точки.Обратите внимание, что в фильтре нельзя смешивать арифметические операции с плавающей запятой и с фиксированной запятой.
Targets
Меню Targets конструктора фильтров позволяет вам генерировать различные типы кода, представляющие ваш фильтр. Например, вы можете генерировать файлы заголовков C, файлы коэффициентов XILINX (COE) (с помощью DSP System Toolbox) и VHDL, Verilog вместе с тестовыми стендами (с помощью Filter Design HDL Coder ™).
Дополнительные функции
Filter Designer также интегрирует дополнительные функции из других продуктов MathWorks ™:
DSP System Toolbox — добавляет расширенные методы проектирования FIR и IIR (т.е.е. Преобразования фильтров, многоскоростные фильтры) и генерирует эквивалентный блок для фильтра
Embedded Coder ™ — генерирует, строит и развертывает код для процессоров Texas Instruments C6000.
Дизайн фильтра HDL Coder — генерирует синтезируемый код VHDL или Verilog для фильтров с фиксированной точкой
Simulink® — генерирует фильтры из атомарных блоков Simulink
A Руководство по SDR и DSP с использованием Python 0 .1 документация
В этой главе представлены фильтры. Мы узнаем о типах фильтров, о том, как фильтры представлены в цифровом виде и как они разработаны. Мы закончим введением в формирование импульса, которое мы подробнее рассмотрим в главе «Формирование импульса».
Основные сведения о фильтрах
Фильтры используются во многих дисциплинах. Например, при обработке изображений широко используются 2D-фильтры, в которых на входе и выходе используются изображения. Вы можете использовать фильтр каждое утро для приготовления кофе, который отфильтровывает твердые частицы из жидкости.В DSP фильтры в основном используются для:
- Разделение сигналов, которые были объединены (например, выделение нужного сигнала)
- Удаление лишних шумов после приема сигнала
- Восстановление сигналов, которые были каким-либо образом искажены (например, эквалайзер звука является фильтром)
Безусловно, фильтры могут использоваться и в других целях, но эта глава предназначена для ознакомления с концепцией, а не для объяснения всех возможных способов фильтрации.
Вы можете подумать, что нас интересуют только цифровые фильтры; в конце концов, этот учебник исследует DSP.Однако важно знать, что многие фильтры будут аналоговыми, как те, что в наших SDR, размещенных перед аналого-цифровым преобразователем (АЦП) на приемной стороне. На следующем изображении схематическая схема аналогового фильтра сопоставлена с блок-схемой алгоритма цифровой фильтрации.
В DSP, где вход и выход являются сигналами, фильтр имеет один входной сигнал и один выходной сигнал:
Невозможно подать два разных сигнала в один фильтр, не сложив их вместе или не выполнив какую-либо другую операцию.Точно так же на выходе всегда будет один сигнал, то есть одномерный массив чисел.
Существует четыре основных типа фильтров: низкочастотный, высокочастотный, полосовой и полосовой. Каждый тип изменяет сигналы, чтобы сосредоточить внимание на различных диапазонах частот внутри них. На графиках ниже показано, как фильтруются частоты в сигналах для каждого типа.
(ДОБАВИТЬ ДИАГРАММУ, ПОКАЗЫВАЮЩУЮ ОТРИЦАТЕЛЬНЫЕ ЧАСТОТЫ)
Каждый фильтр разрешает определенным частотам оставаться в сигнале, блокируя другие частоты.Диапазон частот, который пропускает фильтр, известен как «полоса пропускания», а «полоса задерживания» относится к тому, что блокируется. В случае фильтра нижних частот он пропускает низкие частоты и останавливает высокие частоты, поэтому 0 Гц всегда будет в полосе пропускания. Для фильтра верхних частот и полосового фильтра 0 Гц всегда будет в полосе задерживания.
Не путайте эти типы фильтрации с алгоритмической реализацией фильтра (например, IIR vs FIR). Самый распространенный тип — это фильтр нижних частот (LPF), потому что мы часто представляем сигналы в основной полосе частот.LPF позволяет нам отфильтровать все «вокруг» нашего сигнала, удаляя лишний шум и другие сигналы.
Представление фильтра
Для большинства фильтров, которые мы увидим (известных как фильтры типа FIR или Finite Impulse Response), мы можем представить сам фильтр с помощью одного массива с плавающей запятой. Для фильтров, симметричных в частотной области, эти числа с плавающей запятой будут действительными (а не комплексными), и их обычно нечетное количество. Мы называем этот массив поплавков «фильтрующими кранами». Мы часто используем в качестве обозначения краны для фильтров.Вот пример набора фильтров, которые определяют один фильтр:
ч = [9.92977939e-04 1.08410297e-03 8.51595307e-04 1.64604862e-04 -1.01714338e-03 -2.46268845e-03 -3.58236429e-03 -3.55412543e-03 -1.68583512e-03 2.10562324e-03 6.93100252e-03 1.09302641e-02 1.17766532e-02 7.60955496e-03 -1.639e-03 -1.48306750e-02 -2.69313236e-02 -3.25659606e-02 -2.63400086e-02 -5.04184562e-03 3.08099470e-02 7.64264738e-02 1.23536693e-01 1.62377258e-01 1.84320776e-01 1.84320776e-01 1.62377258e-01 1.23536693e-01 7.64264738e-02 3.08099470e-02 -5.04184562e-03 -2.63400086e-02 -3.25659606e-02 -2.69313236e-02 -1.48306750e-02 -1.
639e-03 7.60955496e-03 1.17766532e-02 1.09302641e-02 6.93100252e-03 2.10562324e-03 -1.68583512e-03 -3.55412543e-03 -3.58236429e-03 -2.46268845e-03 -1.01714338e-03 1.64604862e-04 8.51595307e-04 1.08410297e-03 9.92977939e-04]
Пример использования
Чтобы узнать, как используются фильтры, давайте рассмотрим пример, в котором мы настраиваем наш SDR на частоту существующего сигнала и хотим изолировать его от других сигналов.Помните, что мы сообщаем нашему SDR, на какую частоту настраиваться, но выборки, которые захватывает SDR, находятся в основной полосе частот, что означает, что сигнал будет отображаться с центром около 0 Гц. Нам нужно будет отслеживать, на какую частоту мы сказали SDR настроиться. Вот что мы можем получить:
Поскольку наш сигнал уже сконцентрирован на постоянном токе (0 Гц), мы знаем, что нам нужен фильтр нижних частот. Мы должны выбрать «частоту среза» (также известную как граничная частота), которая будет определять, когда полоса пропускания переходит в полосу задерживания.Частота среза всегда будет в Гц. В этом примере 3 кГц кажется хорошим значением:
Однако, как работает большинство фильтров нижних частот, граница отрицательной частоты также будет составлять -3 кГц. То есть он симметричен относительно постоянного тока (позже вы увидите, почему). Наши частоты среза будут выглядеть примерно так (полоса пропускания — это область между ними):
После создания и применения фильтра с частотой среза 3 кГц теперь имеем:
Этот отфильтрованный сигнал будет выглядеть запутанным, пока вы не вспомните, что наш минимальный уровень шума был на зеленой линии около -65 дБ.Несмотря на то, что мы все еще можем видеть мешающий сигнал с центром на частоте 10 кГц, мы имеем , значительно уменьшив мощность этого сигнала . Теперь он ниже минимального уровня шума! Мы также удалили большую часть шума, который существовал в полосе задерживания.
Помимо частоты среза, другой главный параметр нашего фильтра нижних частот называется «шириной перехода». Ширина перехода, также измеряемая в Гц, указывает фильтру, как быстро он должен переходить между полосой пропускания и полосой задерживания, поскольку мгновенный переход невозможен.
Представим себе ширину перехода. На диаграмме ниже зеленая линия представляет собой идеальный отклик для перехода между полосой пропускания и полосой задерживания, ширина перехода которой по существу равна нулю. Красная линия демонстрирует результат реалистичного фильтра, который имеет некоторую рябь и определенную ширину перехода.
Вы можете спросить, почему мы просто не установили ширину перехода как можно меньше. Причина в основном в том, что меньшая ширина перехода приводит к большему количеству ответвлений, а большее количество ответвлений означает больше вычислений — мы скоро увидим почему.Фильтр с 50 точками может работать весь день, используя 1% ЦП на Raspberry Pi. Между тем, фильтр с 50 000 нажатий приведет к взрыву вашего процессора!
Обычно мы используем инструмент для создания фильтров, затем смотрим, сколько нажатий он выводит, и если их слишком много (например, более 100), мы увеличиваем ширину перехода. Конечно, все зависит от приложения и оборудования, на котором запущен фильтр.
В приведенном выше примере фильтрации мы использовали порог среза 3 кГц и ширину перехода 1 кГц (на самом деле трудно увидеть ширину перехода, просто глядя на эти снимки экрана).Полученный фильтр имел 77 отводов.
Вернуться к представлению фильтра. Несмотря на то, что мы можем показать список отводов для фильтра, мы обычно представляем фильтры визуально в частотной области. Мы называем это «частотной характеристикой» фильтра, и она показывает нам поведение фильтра по частоте. Вот частотная характеристика фильтра, который мы только что использовали:
Обратите внимание, что здесь я показываю , а не сигнал — это просто представление фильтра в частотной области.Поначалу это может быть немного сложно осмыслить, но, когда мы посмотрим на примеры и код, он щелкнет.
Данный фильтр также имеет представление во временной области; это называется «импульсной характеристикой» фильтра, потому что это то, что вы видите во временной области, если вы берете импульс и пропускаете его через фильтр. (Google «Дельта-функция Дирака» для получения дополнительной информации о том, что такое импульс). Для фильтра типа КИХ импульсная характеристика — это просто отводы. Для фильтра с 77 ответвлениями, который мы использовали ранее, количество отводов:
ч = [-0.00025604525581002235, 0,000136698144728, 0,0005385575350373983, 0,0008378280326724052, 0,0002720258534, 0,0006353431381285191, -9.884083502996931e-19, -0.0008822851814329624, -0.0017323142383247614, -0,0021665366366505623, -0,0018335371278226376, -0,00054145673513, 0,0013452467227, 0,0033936649560928345, 0,004703888203948736, 0,004488115198 6, 0,0023609865456819534, -0,0013707970501855016, -0.00564080523326993, -0.0088531385899, -0.009428252466022968, -0,006394983734935522, 4.76480351940553e-18, 0,008114570751786232, 0,015200719237327576, 0,018197273835539818, 0,01482443418353796, 0,004636279307305813, -0,010356673039495945, -0,0257918 208527, -0,03587324544787407, -0,034922562539577484, -0,0123786878586, 0,011919975280761719, 0,05478153005242348, 0,10243935883045197, 0,14588103058, 0,1762896478176117, 0,18720689415931702, 0,1762896478176117, 0,14588103058, 0,10243935883045197, 0,05478153005242348, 0,011919975280761719, -0,0123786878586, -0.034922562539577484, -0.03587324544787407, -0,0257918
208527, -0,010356673039495945, 0,004636279307305813, 0,01482443418353796, 0,018197273835539818, 0,015200719237327576, 0,008114570751786232, 4.76480351940553e-18, -0.006394983734935522, -0.009428252466022968, -0,00885
31385899, -0,00564080523326993, -0,0013707970501855016, 0,0023609865456819534, 0,0044881151986, 0,004703888203948736, 0,0033936649560928345, 0,00134 52467227, -0,00054145673513, -0,0018335371278226376, -0,0021665366366505623, -0,0017323142383247614, -0.0008822851814329624, -9.884083502996931e-19, 0.0006353431381285191, 0,0002720258534, 0,0008378280326724052, 0,0005385575350373983, 0.000136698144728, -0.00025604525581002235] И хотя мы еще не вошли в разработку фильтра, вот код Python, который сгенерировал этот фильтр:
импортировать numpy как np из scipy импортного сигнала импортировать matplotlib.pyplot как plt num_taps = 51 # помогает использовать нечетное количество нажатий cut_off = 3000 # Гц sample_rate = 32000 # Гц # создаем наш фильтр нижних частот h = сигнал.firwin (num_taps, cut_off, nyq = sample_rate / 2) # построить импульсную характеристику plt.plot (h, '.-') plt.show ()Простое построение этого массива чисел с плавающей запятой дает нам импульсную характеристику фильтра:
А вот код, который использовался для получения частотной характеристики, показанной ранее. Это немного сложнее, потому что нам нужно создать массив частот по оси абсцисс.
# построить АЧХ H = np.abs (np.fft.fft (h, 1024)) # берем 1024-точечное БПФ и величину H = np.fft.fftshift (H) # сделать 0 Гц в центре w = np.linspace (-sample_rate / 2, sample_rate / 2, len (H)) # ось x plt.plot (w, H, '.-') plt.show ()Реальные и сложные фильтры
Фильтр, который я вам показал, имел реальные отводы, но отводы также могут быть сложными. Независимо от того, являются ли ответвления настоящими или сложными, не обязательно соответствовать проходящему через него сигналу, то есть вы можете пропустить сложный сигнал через фильтр с настоящими ответвлениями и наоборот. Когда ответвления действительны, частотная характеристика фильтра будет симметричной относительно постоянного тока (0 Гц).Обычно мы используем сложные отводы, когда нам нужна асимметрия, что случается не слишком часто.
В качестве примера сложных ответвлений давайте вернемся к варианту использования фильтрации, за исключением того, что на этот раз мы хотим получить другой мешающий сигнал (без необходимости перенастраивать радио). Это означает, что нам нужен полосовой фильтр, но не симметричный. Мы хотим только поддерживать (также известные как «пропускать») частоты в диапазоне от 7 кГц до 13 кГц (мы не хотим также передавать от -13 кГц до -7 кГц):
Одним из способов создания такого фильтра является создание фильтра нижних частот с частотой среза 3 кГц и последующим его сдвигом по частоте.Помните, что мы можем сдвинуть частоту x (t) (во временной области), умножив его на. В этом случае должно быть 10 кГц, что сдвигает наш фильтр на 10 кГц. Напомним, что в нашем коде Python, приведенном выше, были отводы фильтра нижних частот. Чтобы создать наш полосовой фильтр, нам просто нужно умножить эти отводы на, хотя это включает в себя создание вектора для представления времени на основе нашего периода дискретизации (инверсия частоты дискретизации):
# (h был найден с использованием первого фрагмента кода) # Сдвинуть фильтр по частоте, умножив на exp (j * 2 * pi * f0 * t) f0 = 10e3 # количество сдвинем Ts = 1.0 / sample_rate # период выборки t = np.arange (0.0, Ts * len (h), Ts) # вектор времени. аргументы (начало, остановка, шаг) exponential = np.exp (2j * np.pi * f0 * t) # это по сути сложная синусоида h_band_pass = h * exponential # выполнить сдвиг # построить импульсную характеристику plt.subplot (121) plt.plot (np.real (h_band_pass), '.-') plt.plot (np.imag (h_band_pass), '.-') plt.legend (['реальный', 'воображаемый'], loc = 1) # построить частотную характеристику H = np.abs (np.fft.fft (h_band_pass, 1024)) # берем 1024-точечное БПФ и величину H = np.fft.fftshift (H) # сделать 0 Гц в центре w = np.linspace (-sample_rate / 2, sample_rate / 2, len (H)) # ось x plt.subplot (122) plt.plot (w, H, '.-') plt.xlabel ('Частота [Гц]') plt.show ()Графики импульсной и АЧХ должны выглядеть так:
Поскольку наш фильтр не является симметричным около 0 Гц, он должен использовать сложные ответвления. Поэтому нам нужны две линии для построения этих сложных касаний. То, что мы видим на левом графике выше, по-прежнему является импульсной характеристикой.Наш график частотной характеристики — это то, что действительно подтверждает, что мы создали тот тип фильтра, на который надеялись, где он будет отфильтровывать все, кроме сигнала с центром около 0 Гц. Еще раз помните, что график выше — , а не фактический сигнал: это просто представление фильтра. Это может быть очень запутанным для понимания, потому что, когда вы применяете фильтр к сигналу и строите выходной сигнал в частотной области, во многих случаях он будет выглядеть примерно так же, как и сама частотная характеристика фильтра.
Реализация фильтра
Не будем слишком углубляться в реализацию фильтров. Скорее я сосредотачиваюсь на дизайне фильтров (в любом случае вы можете найти готовые реализации на любом языке программирования). А пока вот один вывод: чтобы отфильтровать сигнал с помощью КИХ-фильтра, вы просто сворачиваете импульсную характеристику (массив отводов) с входным сигналом. (Не волнуйтесь, свертка объясняется в следующем разделе.) В дискретном мире мы используем дискретную свертку (пример ниже).Треугольники, обозначенные буквой b, — это отводы. На блок-схеме квадраты, помеченные над треугольниками, означают задержку на один временной шаг.
Возможно, вы поймете, почему мы сейчас называем их фильтрами «отводы», исходя из того, как реализован сам фильтр.
РПИ и ИИР
Существует два основных класса цифровых фильтров: КИХ и БИХ
- Конечная импульсная характеристика (FIR)
- Бесконечная импульсная характеристика (IIR)
Мы не будем углубляться в теорию, а пока просто запомните: FIR-фильтры проще в разработке и могут делать все, что вы хотите, если вы используете достаточное количество нажатий.БИХ-фильтры более сложны и потенциально могут быть нестабильными, но они более эффективны (используют меньше ЦП и памяти для данного фильтра). Если кто-то просто дает вам список отводов, предполагается, что это отводы для КИХ-фильтра. Если они начинают упоминать «полюса», они говорят о БИХ-фильтрах. В этом учебнике мы будем придерживаться КИХ-фильтров.
Ниже приведен пример частотной характеристики, в котором сравниваются КИХ и БИХ-фильтры, которые выполняют почти одинаковую фильтрацию; у них аналогичная ширина перехода, которая, как мы узнали, будет определять, сколько потребуется ответвлений.КИХ-фильтр имеет 50 отводов, а БИХ-фильтр — 12 полюсов, что с точки зрения требуемых вычислений похоже на 12 отводов.
Урок состоит в том, что КИХ-фильтр требует значительно больше вычислительных ресурсов, чем БИХ-фильтр, для выполнения примерно такой же операции фильтрации.
Вот несколько реальных примеров FIR- и IIR-фильтров, которые вы, возможно, использовали раньше.
Если вы выполняете «скользящее среднее» по списку чисел, это просто КИХ-фильтр с нажатиями на единицы:
— h = [1 1 1 1 1 1 1 1 1 1] для фильтра скользящего среднего с размером окна 10.Это также фильтр нижних частот; это почему? В чем разница между использованием единиц и ответами, которые затухают до нуля?Ответы
Фильтр скользящего среднего — это фильтр нижних частот, потому что он сглаживает «высокочастотные» изменения, поэтому обычно люди его и используют. Причина использования ответвлений, которые затухают до нуля на обоих концах, состоит в том, чтобы избежать внезапного изменения выходного сигнала, например, если бы фильтруемый сигнал какое-то время был нулевым, а затем внезапно подскочил.
Теперь пример БИХ.Кто-нибудь из вас когда-либо делал это:
x = x * 0,99 + новое_значение * 0,01
, где 0,99 и 0,01 представляют скорость обновления значения (или скорость убывания, то же самое). Это удобный способ медленно обновлять какую-либо переменную, не запоминая несколько последних значений. На самом деле это разновидность БИХ-фильтра нижних частот. Надеюсь, вы понимаете, почему БИХ-фильтры обладают меньшей стабильностью, чем КИХ. Ценности никогда не исчезают полностью!
Свертка
Сделаем небольшое отступление, чтобы познакомить вас с оператором свертки.Не стесняйтесь пропустить этот раздел, если вы уже знакомы с ним.
Сложение двух сигналов — это один из способов объединения двух сигналов в один. В главе «Частотная область» мы исследовали, как свойство линейности применяется при сложении двух сигналов вместе. Свертка — это еще один способ объединить два сигнала в один, но он сильно отличается от простого их добавления. Свертка двух сигналов похожа на скольжение друг по другу и интеграцию. Это очень похоже на на взаимную корреляцию, если вы знакомы с этой операцией.Фактически во многих случаях это эквивалентно взаимной корреляции.
Я считаю, что операцию свертки лучше всего изучить на примерах. В этом первом примере мы сворачиваем два прямоугольных импульса вместе:
Поскольку это просто скользящее интегрирование, в результате получается треугольник с максимумом в точке, где оба прямоугольных импульса идеально совпадают. Давайте посмотрим, что произойдет, если мы свернем прямоугольный импульс с треугольным:
В обоих примерах у нас есть два входных сигнала (один красный, один синий), а затем отображается выходной сигнал свертки.Вы можете видеть, что на выходе получается объединение двух сигналов, когда один скользит по другому. Из-за этого «скользящего» характера длина вывода на самом деле больше, чем длина ввода. Если один сигнал составляет
Mотсчетов, а другой сигнал —Nотсчетов, свертка двух может датьN + M-1отсчетов. Однако такие функции, какnumpy.convolve (), имеют способ указать, нужен ли вам весь вывод (max (M, N),образцов) или только образцы, в которых сигналы полностью перекрываются (max (M, N) ) - min (M, N) + 1, если вам было интересно).Не нужно вдаваться в подробности. Просто знайте, что длина вывода свертки — это не только длина входных данных.Так почему свертка важна в DSP? Для начала, чтобы отфильтровать сигнал, мы можем просто взять импульсную характеристику этого фильтра и свернуть ее с сигналом. КИХ-фильтрация — это просто операция свертки.
Это может сбивать с толку, потому что ранее мы упоминали, что свертка принимает два сигнала и выводит один.Мы можем рассматривать импульсную характеристику как сигнал, а свертка — это, в конце концов, математический оператор, который работает с двумя одномерными массивами. Если один из этих одномерных массивов является импульсной характеристикой фильтра, другой одномерный массив может быть частью входного сигнала, а выход будет отфильтрованной версией входного сигнала.
Давайте посмотрим на другой пример, чтобы помочь с этим щелчком. В приведенном ниже примере треугольник будет представлять импульсную характеристику нашего фильтра, а зеленый сигнал — это наш сигнал, который фильтруется.
Красный выход — это отфильтрованный сигнал.
Вопрос: Какой тип фильтра был треугольником?
Answers
Он сглаживает высокочастотные компоненты зеленого сигнала (то есть резкие переходы квадрата), поэтому он действует как фильтр нижних частот.
Теперь, когда мы начинаем понимать свертку, я представлю для нее математическое уравнение. Звездочка (*) обычно используется как символ свертки:
В приведенном выше выражении — это сигнал или вход, который переворачивается и скользит по горизонтали, но его можно менять местами, и это все равно то же выражение.Как правило, более короткий массив будет использоваться как. Свертка равна взаимной корреляции, определяемой как, когда она симметрична, то есть не меняется при повороте относительно начала координат.
Дизайн фильтра
на Python
Теперь мы рассмотрим один из способов самостоятельно разработать КИХ-фильтр на Python. Хотя существует множество подходов к разработке фильтров, мы будем использовать метод, начиная с частотной области и работая в обратном направлении, чтобы найти импульсную характеристику. В конечном итоге именно так и представлен наш фильтр (его краны).
Вы начинаете с создания вектора желаемой частотной характеристики. Давайте спроектируем фильтр нижних частот произвольной формы, показанный ниже:
Код, используемый для создания этого фильтра, довольно прост:
импортировать numpy как np импортировать matplotlib.pyplot как plt H = np.hstack ((np.zeros (20), np.arange (10) / 10, np.zeros (20))) w = np.linspace (-0,5; 0,5; 50) plt.plot (w, H, '.-') plt.show ()
hstack ()— это один из способов объединения массивов в numpy. Мы знаем, что это приведет к фильтру со сложными отводами.Почему?Ответ
Это несимметрично около 0 Гц.
Наша конечная цель — найти отводы этого фильтра, чтобы мы могли его действительно использовать. Как получить ответвления, учитывая частотную характеристику? Ну, как нам преобразовать из частотной области обратно во временную? Обратное БПФ (ОБПФ)! Напомним, что функция IFFT почти такая же, как и функция FFT. Нам также необходимо выполнить IFFT-сдвиг желаемой частотной характеристики перед IFFT, а затем нам понадобится еще один IFF-сдвиг после IFFT (нет, они не отменяются, вы можете попробовать).Этот процесс может показаться запутанным. Просто помните, что вы всегда должны выполнять FFTshift после FFT и IFFshift после IFFT.
h = np.fft.ifftshift (np.fft.ifft (np.fft.ifftshift (H))) plt.plot (np.real (h)) plt.plot (np.imag (h)) plt.legend (['реальный', 'воображаемый'], loc = 1) plt.show ()Мы будем использовать эти отводы, показанные выше, в качестве нашего фильтра. Мы знаем, что импульсная характеристика отображает ответвления, поэтому то, что мы видим выше , — это наша импульсная характеристика. Давайте возьмем БПФ наших нажатий, чтобы увидеть, как на самом деле выглядит частотная область.Мы сделаем 1024 точки БПФ, чтобы получить высокое разрешение:
H_fft = np.fft.fftshift (np.abs (np.fft.fft (h, 1024))) plt.plot (H_fft) plt.show ()Посмотрите, что частотная характеристика не очень прямая … она не очень хорошо соответствует нашему оригиналу, если вы вспомните форму, для которой мы изначально хотели создать фильтр. Большая причина в том, что наша импульсная характеристика не перестает затухать, то есть левая и правая стороны не достигают нуля. У нас есть два варианта, которые позволят ему упасть до нуля:
Вариант 1: Мы «закрываем» нашу текущую импульсную характеристику так, чтобы она уменьшалась до 0 с обеих сторон.Он включает в себя умножение нашей импульсной характеристики на «оконную функцию», которая начинается и заканчивается на нуле.
# После создания h с помощью предыдущего кода создайте и примените окно окно = np.hamming (len (h)) h = h * окноВариант 2: Мы повторно генерируем нашу импульсную характеристику, используя большее количество точек, чтобы у нее было время затухать. Нам нужно добавить разрешение к нашему исходному массиву частотной области (так называемая интерполяция).
H = np.hstack ((np.zeros (200), np.arange (100) / 100, np.нули (200))) w = np.linspace (-0,5; 0,5; 500) plt.plot (w, H, '.-') plt.show () # (остальной код тот же)Оба варианта работали. Какой бы вы выбрали? Второй метод привел к большему количеству нажатий, но первый метод привел к не очень резкой частотной характеристике и не очень крутому спаду. Существует множество способов создания фильтра, каждый со своими компромиссами. Многие считают проектирование фильтров искусством.
Введение в формирование импульса
Мы кратко представим очень интересную тему DSP — формирование импульсов.Мы рассмотрим эту тему более подробно в отдельной главе позже, см. «Формирование импульса». Это стоит упомянуть наряду с фильтрацией, потому что формирование импульса — это, в конечном счете, тип фильтра, используемого для определенной цели, со специальными свойствами.
Как мы узнали, цифровые сигналы используют символы для представления одного или нескольких битов информации. Мы используем схему цифровой модуляции, такую как ASK, PSK, QAM, FSK и т. Д., Чтобы модулировать несущую, чтобы информацию можно было отправлять по беспроводной сети. Когда мы моделировали QPSK в главе «Цифровая модуляция», мы моделировали только одну выборку на символ, т.е.е., каждое созданное нами комплексное число было одной из точек созвездия — это был один символ. На практике мы обычно генерируем несколько выборок для каждого символа, и причина кроется в фильтрации.
Мы используем фильтры для создания «формы» наших символов, потому что форма во временной области меняет форму в частотной области. Частотная область сообщает нам, какой спектр / полосу пропускания будет использовать наш сигнал, и мы обычно хотим минимизировать его. Важно понимать, что спектральные характеристики (частотная область) символов основной полосы частот не изменяются, когда мы модулируем несущую; он просто сдвигает основную полосу вверх по частоте, в то время как форма остается прежней, что означает, что объем используемой полосы пропускания остается прежним.Когда мы используем 1 отсчет на символ, это похоже на передачу прямоугольных импульсов. Фактически, BPSK с использованием 1 выборки на символ — это , просто квадратная волна из случайных единиц и -1:
И, как мы узнали, прямоугольные импульсы неэффективны, потому что они используют избыточное количество спектра:
Таким образом, мы «формируем импульс» для этих блочно-выглядящих символов, чтобы они занимали меньшую полосу пропускания в частотной области. Мы «формируем импульс», используя фильтр нижних частот, потому что он отбрасывает высокочастотные компоненты наших символов.Ниже показан пример символов во временной (вверху) и частотной (внизу) областях до и после применения фильтра формирования импульсов:
Обратите внимание, насколько быстрее сигнал падает по частоте. Боковые лепестки ниже на ~ 30 дБ после формирования импульса; это в 1000 раз меньше! И что еще более важно, главный лепесток уже, поэтому для того же количества бит в секунду используется меньший спектр.
На данный момент имейте в виду, что распространенные фильтры формирования импульсов включают:
- Фильтр приподнятого косинуса
- Корневой фильтр с приподнятым косинусом
- Sinc фильтр
- Фильтр Гаусса
Эти фильтры обычно имеют параметр, который можно настроить для уменьшения используемой полосы пропускания.Ниже показаны временная и частотная области фильтра с приподнятым косинусом с различными значениями параметра, определяющего крутизну спада.
Вы можете видеть, что меньшее значение уменьшает используемый спектр (для того же объема данных). Однако, если значение слишком низкое, тогда символам временной области требуется больше времени, чтобы спадать до нуля. Фактически, когда символы никогда полностью не распадаются до нуля, что означает, что мы не можем передавать такие символы на практике. Обычно значение около 0,35.
Вы узнаете намного больше о формировании импульсов, включая некоторые специальные свойства, которым должны удовлетворять фильтры формирования импульсов, в главе «Формирование импульсов».
Руководство для ученых и инженеров по цифровой обработке сигналов Стивен В. Смит, доктор философии.
Цифровые фильтры — очень важная часть DSP. Фактически, их необыкновенные
производительность — одна из ключевых причин того, что DSP стал таким популярным. В виде
Упомянутые во введении фильтры имеют два применения: разделение сигнала , и
сигнал восстановление . Разделение сигналов необходимо, когда сигнал был
загрязнены помехами, шумом или другими сигналами.Например, представьте
прибор для измерения электрической активности сердца ребенка (ЭКГ), пока он еще
в утробе матери. Необработанный сигнал, вероятно, будет искажен дыханием и
сердцебиение матери. Для разделения этих сигналов можно использовать фильтр, чтобы
их можно анализировать индивидуально.Восстановление сигнала используется, когда сигнал был каким-либо образом искажен. Для
Например, аудиозапись, сделанная с использованием плохого оборудования, может быть отфильтрована для улучшения
представляют звук в том виде, в каком он действительно произошел.Другой пример — снятие размытия.
изображения, полученного неправильно сфокусированным объективом или шаткой камерой.Эти проблемы можно решить с помощью аналоговых или цифровых фильтров. Который
лучше? Аналоговые фильтры дешевы, быстры и имеют большой динамический диапазон в обоих случаях.
амплитуда и частота. Для сравнения, цифровые фильтры значительно превосходят
уровень производительности, который может быть достигнут. Например, низкочастотный цифровой
Фильтр, представленный в главе 16, имеет коэффициент усиления 1 +/- 0.0002 от постоянного тока до 1000 герц,
и коэффициент усиления менее 0,0002 для частот выше 1001 герц. Целиком
переход происходит в пределах всего 1 герца. Не ожидайте этого от схемы операционного усилителя!
Цифровые фильтры могут обеспечить производительность в тысяч раз лучше, чем у аналоговых.
фильтры. Это кардинально влияет на то, как возникают проблемы с фильтрацией.
подошел. При использовании аналоговых фильтров упор делается на устранение ограничений
электроника, такая как точность и стабильность резисторов и конденсаторов.Для сравнения, цифровые фильтры настолько хороши, что производительность фильтра невысока.
часто игнорируется. Акцент смещается на ограничения сигналов , а
теоретических, вопросов по их обработке.В DSP принято говорить, что входные и выходные сигналы фильтра находятся в интервале времени .
домен . Это связано с тем, что сигналы обычно создаются путем дискретизации на регулярной основе.
интервалы время . Но это не единственный способ отбора проб.В
Второй наиболее распространенный способ выборки — через равные интервалы в пространстве . Для
Например, представьте себе одновременное снятие показаний с массива тензодатчиков.
устанавливается с шагом в один сантиметр по длине крыла самолета.
Возможны многие другие домены; тем не менее, время и пространство, безусловно, самые
общий. Когда вы видите термин временной области в DSP, помните, что он может
фактически относятся к образцам, взятым с течением времени, или это может быть общая ссылка на любые
домен, в котором берутся образцы.Как показано на рис. 14-1, каждый линейный фильтр имеет импульсную характеристику, ступенчатую
отклик и частотная характеристика. Каждый из этих ответов содержит полные
информация о фильтре, но в другой форме. Если один из трех
указано, два других фиксированы и могут быть рассчитаны напрямую. Все три
эти представления важны, потому что они описывают, как фильтр будет
реагируют при разных обстоятельствах.Самый простой способ реализовать цифровой фильтр — это свертка
входной сигнал с импульсной характеристикой цифрового фильтра .Все возможные линейные фильтры
можно сделать таким образом. (Это должно быть очевидно. Если это не так, вы, вероятно,
у вас нет подготовки, чтобы понять этот раздел о дизайне фильтров. Пытаться
повторяя предыдущий раздел об основах DSP). Когда импульс
ответ используется таким образом, разработчики фильтров дают ему специальное имя: фильтр
ядро.Существует также другой способ создания цифровых фильтров, называемый рекурсией. Когда фильтр
реализуется путем свертки, каждая выборка на выходе вычисляется по
взвешивает выборок на входе и складывает их вместе.Рекурсивные фильтры
являются расширением этого, используя ранее рассчитанные значения из вывода ,
помимо точек из ввода . Вместо использования ядра фильтра рекурсивные фильтры
определяются набором коэффициентов рекурсии. Об этом методе и пойдет речь.
подробно в Главе 19. На данный момент важно, чтобы все линейные фильтры
иметь импульсный отклик, даже если вы не используете его для реализации фильтра. К
найти импульсную характеристику рекурсивного фильтра, просто подать импульс и
посмотрим, что получится.Импульсные характеристики рекурсивных фильтров складываются
синусоид, которые экспоненциально затухают по амплитуде. В принципе, это делает их
импульсные характеристики бесконечно длинные . Однако со временем амплитуда падает.
ниже шума округления системы, а остальные отсчеты могут быть
игнорируется. Потому чтоэтой характеристики рекурсивные фильтры также называются бесконечной импульсной характеристикой.
или БИХ-фильтры. Для сравнения, фильтры, выполняемые сверткой, называются Finite
Импульсная характеристика или КИХ-фильтры.Как вы знаете, импульсная характеристика является выходом системы, когда на входе
импульс . Таким же образом, переходная характеристика является выходом, когда вход
это шаг (также называемый кромкой и откликом кромки ). Поскольку ступенька
интеграл импульса, переходная характеристика является интегралом импульсной характеристики.
Это дает два способа найти ступенчатую характеристику: (1) подать ступенчатую форму волны в
фильтр и посмотреть, что получится, или (2) интегрировать импульсную характеристику.(Быть
математически правильно: интегрирование используется с непрерывными сигналами, а
(дискретное интегрирование (), т.е. текущая сумма, используется с дискретными сигналами). В
частотную характеристику можно найти, взяв ДПФ (используя алгоритм БПФ)
импульсной характеристики. Это будет рассмотрено позже в этой главе. В
частотная характеристика может быть нанесена на линейную вертикальную ось, например, в (c), или на
логарифмическая шкала (децибелы), как показано на (d).Линейная шкала лучше всего подходит для
показывает пульсацию и спад полосы пропускания, а шкала децибел необходима для
показать затухание в полосе задерживания.Не помните децибелы? Вот краткий обзор. Бел (в честь
Александр Грэхем Белл) означает, что мощность изменяется на коэффициент , равный десяти . Для
Например, электронная схема с 3 белками усиления производит
выходной сигнал с мощностью в 10 × 10 × 10 = 1000 раз больше входной. Децибел
(дБ) составляет одну десятую бел.Следовательно, значения децибел: -20 дБ, -10 дБ, 0 дБ,
10 дБ и 20 дБ означают отношения мощности: 0,01, 0,1, 1, 10 и 100 соответственно. В
Другими словами, каждые десять децибел означают, что мощность изменилась в раз
десять.Вот загвоздка: обычно вы хотите работать с сигналом с амплитудой , а не с его
мощность . Например, представьте себе усилитель с усилением 20 дБ. По определению,
это означает, что мощность сигнала увеличилась в 100 раз.С
амплитуда пропорциональна квадратному корню из мощности, амплитуда
выходная амплитуда в 10 раз больше входной. В то время как 20 дБ означает коэффициент 100
по мощности это означает только 10 раз по амплитуде. Каждые двадцать децибел означают
что амплитуда изменилась в десять раз. В форме уравнения:В приведенных выше уравнениях используется десятичный логарифм; однако многие компьютерные
языки предоставляют функцию только для логарифма с основанием и (натуральный логарифм,
письменный журнал e x или ln x ).Натуральный логарифм можно использовать, изменив приведенные выше уравнения: дБ = 4,342945 log e ( P 2 / P 1 ) и дБ = 8,685890 log e ( A 2 / A 1 ).Поскольку децибелы являются способом выражения отношения между двумя сигналами, они
идеально подходит для описания коэффициента усиления системы, т. е. отношения между выходом и
входной сигнал. Однако инженеры также используют децибелы для определения амплитуды.
(или мощность) одиночного сигнала , ссылаясь на какой-то стандарт.Например,
термин: дБВ означает, что сигнал соотносится со среднеквадратичным значением 1 В.
Аналогичным образом, дБм означает, что опорный сигнал дает 1 мВт на 600 Ом.
нагрузка (около 0,78 В, действующее значение).Если вы больше ничего не понимаете в децибелах, запомните две вещи: во-первых, -3 дБ означает, что амплитуда снижена до 0,707 (и, следовательно, мощность
снижено до 0,5). Во-вторых, запомните следующие преобразования децибел
и соотношения амплитуды :Проектирование аналогового фильтра
: раскрытие тайны | Максим Интегрированный
Аннотация: В этой статье показано, как создавать аналоговые фильтры.Он начинается с изучения основ фильтров, затем знакомит с основными типами фильтров, такими как Баттерворт, Чебышев и Бессель, а затем проводит читателя через процесс разработки фильтров нижних и верхних частот. Включены вывод уравнений и схемная реализация.
Там джунгли.
Небольшое племя, живущее в густой пустыне, пользуется большим спросом у охотников за головами с окрестных равнин. Известное по всей стране своим эзотерическим опытом, это племя Аналоговых Инженеров, которые живут в самых дальних регионах левой половины Равнин, за джунглями Лапласа.
Гуру аналоговых инженеров — конструктор аналоговых фильтров, который восседает на троне своего королевства и делится мудростью. Вы никогда не увидите его, даже по предварительной записи, и вы называете его «сэр».
Бесчисленные страницы уравнений, которые можно найти в большинстве книг по проектированию фильтров, могут напугать маленьких собак и цифровых дизайнеров. Эта статья прокладывает путь практическому инженеру и раскрывает тайну конструкции фильтра, позволяя быстро и с минимумом математических вычислений конструировать аналоговые фильтры непрерывного действия.
Теория аналоговой электроники
У аналоговой электроники есть две разные стороны: теория, преподаваемая академическими учреждениями (уравнения устойчивости, расчеты фазового сдвига и т. Д.), И практическая сторона, знакомая большинству инженеров (избегайте колебаний, настраивая коэффициент усиления с помощью конденсатора и т. К сожалению, конструкция фильтра прочно основана на давно установленных уравнениях и таблицах теоретических результатов. Конструкция фильтра на основе теоретических уравнений может оказаться сложной задачей. Следовательно, это обсуждение использует минимум математики — либо для перевода теоретических таблиц в практические значения компонентов, либо для получения отклика фильтра общего назначения.
Основы
Простые RC-фильтры нижних частот имеют передаточную функцию:
Каскадирование таких фильтров усложняет реакцию, приводя к квадратным уравнениям в знаменателе передаточной функции. Таким образом, знаменатель передаточной функции любого фильтра нижних частот второго порядка равен as² + bs + c. Подстановка значений для a, b и c определяет отклик фильтра по частоте. Любой, кто помнит математику средней школы, заметит, что приведенное выше выражение равно нулю для определенных значений «s», задаваемых уравнением:
При значениях «s», для которых это квадратное уравнение равно нулю, передаточная функция теоретически имеет бесконечный выигрыш.Эти значения, которые определяют производительность каждого типа фильтра по частоте, известны как полюса квадратного уравнения. Полюсы обычно встречаются парами в форме комплексного числа (a + jb) и его комплексно сопряженного числа (a — jb). Член jb иногда равен нулю.
Мысль о передаточной функции с бесконечным усилением может напугать нервных читателей, но на практике это не проблема. Действительная часть полюса «а» указывает, как фильтр реагирует на переходные процессы, а его мнимая часть «jb» указывает отклик по частоте.Пока эта действительная часть отрицательна, система стабильна. В следующем тексте объясняется, как преобразовать таблицы полюсов, найденные во многих учебниках, в значения компонентов, подходящие для проектирования схем.
Типы фильтров
Наиболее распространены ответы фильтров типа Баттерворта, Чебышева и Бесселя. Доступно много других типов, но 90% всех приложений можно решить с помощью одного из этих трех. Баттерворт обеспечивает ровный отклик в полосе пропускания и адекватную скорость спада.Хороший универсальный фильтр Баттерворта прост для понимания и подходит для таких приложений, как обработка звука. Чебышев дает гораздо более крутой спад, но пульсация полосы пропускания делает его непригодным для аудиосистем. Он лучше всего подходит для приложений, в которых полоса пропускания включает только одну интересующую частоту (например, получение синусоидальной волны из прямоугольной волны путем фильтрации гармоник).
Фильтр Бесселя дает постоянную задержку распространения по входному частотному спектру.Следовательно, подача прямоугольной волны (состоящей из основной гармоники и множества гармоник) на вход фильтра Бесселя дает выходную прямоугольную волну без выброса (все частоты задерживаются на одинаковую величину). Другие фильтры задерживают гармоники на разную величину, что приводит к выбросу выходного сигнала. Другой популярный фильтр, эллиптический тип, является гораздо более сложным фильтром, который не будет обсуждаться в этом тексте. Подобно ответу Чебышева, у него есть пульсация в полосе пропускания и серьезный спад за счет пульсации в полосе задерживания.
Стандартные фильтрующие блоки
Общая структура фильтра (, рис. 1a, ) позволяет реализовать схему пропускания верхних или нижних частот путем замены конденсаторов или резисторов вместо компонентов с G1 по G4. Учитывая влияние этих компонентов на цепь обратной связи операционного усилителя, можно легко получить фильтр нижних частот, превратив G2 / G4 в конденсаторы, а G1 / G3 в резисторы. (Выполнение обратного дает реализацию highpass.)
Рисунок 1. Заменяя G1 на G4 в общем блоке фильтров (a), вы можете реализовать фильтр lowpass (b) или фильтр highpass (c).
Передаточная функция для фильтра нижних частот (рисунок 1b):
Это уравнение проще с проводимостью. Замените конденсаторы с проводимостью sC, а резисторы с проводимостью G. Если это кажется сложным, вы можете «нормализовать» уравнение. Установите резисторы на 1 Ом или конденсаторы на 1Ф и измените окружающие компоненты, чтобы они соответствовали отклику. Таким образом, при всех значениях резисторов, равных 1 Ом, передаточная функция нижних частот будет:
Эта передаточная функция описывает отклик стандартного фильтра нижних частот второго порядка.Теперь мы возьмем теоретические таблицы полюсов, которые описывают три основных отклика фильтра, и переведем их в реальные значения компонентов.
Процесс проектирования
Чтобы определить тип необходимого фильтра, вы должны использовать приведенные выше описания для выбора необходимой производительности полосы пропускания. Самый простой способ определить порядок фильтрации — разработать каскад фильтра 2-го порядка, а затем при необходимости каскадировать несколько его версий. Проверьте, дает ли результат желаемое отклонение полосы задерживания, а затем перейдите к правильному расположению полюсов, как показано в таблицах в Приложении .Как только положения полюсов будут установлены, значения компонентов можно будет вскоре вычислить.
Во-первых, преобразуйте положение каждого полюса в квадратичное выражение, аналогичное выражению в знаменателе нашего общего фильтра 2-го порядка. Если квадратное уравнение имеет полюсы из (a ± jb), то оно имеет корни из (s — a — jb) и (s — a + jb). Когда эти корни перемножаются, получается квадратное выражение s² — 2as + a² + b².
В таблицах полюсов «a» всегда отрицательно, поэтому для удобства мы объявляем s² + 2as + a² + b² и используем величину «a» независимо от его знака.Чтобы применить это на практике, рассмотрим фильтр Баттерворта 4-го порядка. Полюса и квадратичное выражение, соответствующие каждому положению полюса, следующие:
Полюса (a ± jb) Квадратичное выражение -0,9239 ± j0,3827 сек² + 1,8478 сек + 1 -0,3827 ± j0,9239 сек² + 0,7654 сек + 1 Используя эту информацию, вы можете разработать фильтр нижних частот Баттерворта 4-го порядка. Просто подставьте значения из приведенных выше квадратных выражений в знаменатель уравнения 4.Таким образом, C2C4 = 1 и 2C4 = 1,8478 в первом фильтре, что означает, что C4 = 0,9239F и C2 = 1,08F. Для второго фильтра C2C4 = 1 и 2C4 = 0,7654, что означает, что C4 = 0,3827F и C2 = 2,61F. Все резисторы в обоих фильтрах равны 1 Ом. Каскадирование этих двух фильтров 2-го порядка дает отклик Баттерворта 4-го порядка с частотой спада 1 рад / с, но значения компонентов невозможно найти. Если указанные выше значения частоты или компонентов не подходят, читайте дальше.
Бывает, что если выдержать соотношение реактивных сопротивлений к резисторам, отклик схемы не изменится.Поэтому вы можете выбрать резисторы 1 кОм. Чтобы гарантировать, что реактивные сопротивления увеличиваются в той же пропорции, что и сопротивления, разделите номиналы конденсаторов на 1000.
У нас все еще есть идеальный отклик Баттерворта, но, к сожалению, частота спада составляет 1рад / с. Чтобы изменить частотную характеристику схемы, мы должны поддерживать отношение реактивных сопротивлений к сопротивлениям, но просто на другой частоте. Для спада 1 кГц, а не 1рад / с, емкость конденсатора должна быть дополнительно уменьшена в 2π × 1000 раз.Таким образом, реактивное сопротивление конденсатора не достигает исходного (нормированного) значения до более высокой частоты. Результирующий фильтр нижних частот Баттерворта 4-го порядка со спадом 1 кГц принимает форму , рис. 2, .
Рис. 2. Эти две неидентичные секции фильтра 2-го порядка образуют фильтр нижних частот Баттерворта 4-го порядка.
Используя описанную выше методику, вы можете получить любой отклик фильтра четного порядка путем каскадирования фильтров 2-го порядка. Обратите внимание, однако, что фильтр Баттерворта 4-го порядка не получается простым вычислением компонентов для фильтра 2-го порядка и последующим каскадным соединением двух таких ступеней.Необходимо разработать два фильтра 2-го порядка, каждый с разным расположением полюсов. Если фильтр имеет нечетный порядок, вы можете просто каскадировать фильтры 2-го порядка и добавить RC-цепь, чтобы получить дополнительный полюс. Например, фильтр Чебышева 5-го порядка с пульсацией 1 дБ имеет следующие полюса:
Полюса Квадратичное выражение -0,2265 ± j0,5918 с² + 0,453 с + 0,402 2,488 с² + 1,127 с + 1 -0,08652 ± j0,9575 с² + 0.173 с + 0,924 1,08 с² + 0,187 с + 1 -0,2800 см. Текст Чтобы обеспечить соответствие общему фильтру, описываемому уравнением 4, и гарантировать, что последний член равен единице, первые две квадратичные величины были умножены на константу. Таким образом, в первом фильтре C2C4 = 2,488 и 2C4 = 1,127, что означает, что C4 = 0,5635F и C2 = 4,41F. Для второго фильтра C2C4 = 1,08 и 2C4 = 0,187, что означает, что C4 = 0,0935F и C2 = 11,55F.
Ранее было показано, что RC-цепь имеет полюс, когда 1 + sCR = 0: s = -1 / CR.Если R = 1, то для получения последнего полюса при s = -0,28 необходимо установить C = 3,57F. Используя резисторы 1 кОм, вы можете нормализовать частоту спада 1 кГц, как показано на Рисунок 3 . Таким образом, дизайнеры могут смело создавать фильтры нижних частот любого порядка на любой частоте.
Рисунок 3. Чебышевский фильтр нижних частот 5-го порядка с пульсацией 1 дБ состоит из двух неидентичных секций 2-го порядка и выходной RC-цепи.
Вся эта теория применима также к конструкции фильтров верхних частот.Было показано, что простой RC-фильтр нижних частот имеет передаточную функцию:
Аналогичным образом простой RC-фильтр верхних частот имеет передаточную функцию:
Нормализация этих функций в соответствии с нормализованными таблицами полюсов дает TF = 1 / (1 + s) для низких частот и TF = 1 / (1 + 1 / s) для высоких частот.
Обратите внимание, что положения полюсов пропускания верхних частот «s» могут быть получены путем инвертирования положений полюсов прохода нижних частот. Вставка этих значений в блок фильтра верхних частот обеспечивает правильную частотную характеристику.Чтобы получить передаточную функцию для блока фильтра верхних частот, нам нужно вернуться к передаточной функции блока фильтра нижних частот. Таким образом, из
мы получаем передаточную функцию эквивалентного блока фильтра верхних частот путем замены конденсаторов и резисторов:
Опять же, жизнь намного проще, если конденсаторы нормализованы вместо резисторов:
Уравнение 9 — это передаточная функция блока фильтра верхних частот. На этот раз мы рассчитываем номиналы резисторов, а не конденсаторов.Учитывая общий отклик фильтра верхних частот, мы можем получить положения полюсов фильтра верхних частот, инвертируя положения полюсов фильтра нижних частот и продолжая, как и раньше. Однако легче сказать, чем сделать инверсию сложного полюса. В качестве примера рассмотрим рассмотренный ранее фильтр Чебышева 5-го порядка с пульсацией 1 дБ. Он имеет два полюсных положения (-0,2265 ± j0,5918).
Самый простой способ инвертировать комплексное число — это умножить и разделить комплексное сопряжение, таким образом получив действительное число в числителе.Затем вы найдете обратную величину, инвертируя дробь следующим образом:
Инвертирование этого выражения дает положения полюсов, которые затем могут быть преобразованы в соответствующее квадратичное выражение, и значения рассчитываются, как и раньше. Результат:
Поляки Квадратичное выражение -0,564 ± j1,474 с² + 1,128 с + 2,490 0,401 с² + 0,453 с + 1 Из уравнения 2 мы можем вычислить значения компонентов первого фильтра как R2R4 = 0.401 и 2R2 = 0,453, что означает, что R2 = 0,227 Ом и R4 = 1,77 Ом. Затем эту процедуру можно повторить для других полюсов.
Поскольку было показано, что s = -1 / CR, более простым подходом является разработка фильтра нижних частот с использованием подходящих полюсов нижних частот, а затем обработка каждого полюса в фильтре как единой RC-цепи. Чтобы инвертировать каждый полюс lowpass, чтобы получить соответствующий полюс highpass, просто инвертируйте значение CR. После определения расположения полюсов фильтра верхних частот мы обеспечиваем правильную частотную характеристику, вставляя конденсаторы и резисторы.
Нормированное значение конденсатора было рассчитано для реализации с фильтром нижних частот, предполагая, что R = 1 Ом. Следовательно, значение CR равно значению C, а величина, обратная значению C, является полюсом верхних частот. Рассмотрение этого полюса как нового значения R дает соответствующее значение высокочастотного компонента.
Рассматривая снова фильтр нижних частот Чебышева 5-го порядка с пульсацией 1 дБ, расчетные значения конденсатора составляют C4 = 0,5635F и C2 = 4,41F. Чтобы получить эквивалентные значения резистора верхних частот, инвертируйте значения C (для получения местоположения полюсов верхних частот) и рассматривайте эти полюса как новые нормированные значения резистора: R4 = 1.77 и R2 = 0,227. Этот подход дает те же результаты, что и более формальный метод, упомянутый ранее.
Таким образом, схема, показанная на Рисунке 3, теперь может быть преобразована в фильтр верхних частот со спадом 1 кГц путем инвертирования нормированных значений конденсаторов, вставки резисторов и конденсаторов и соответствующего масштабирования значений. Ранее мы разделили на 2πfR, чтобы нормализовать значения низких частот. Коэффициент масштабирования в этом случае равен 2πfC, где C — емкость конденсатора, а f — частота в герцах. В результате получается схема , рисунок 4, , а моделирование SPICE показывает ожидаемые характеристики на выходе каждого фильтра (, рисунок 5, ).
Рис. 4. Перестановка резисторов и конденсаторов в схеме на рис. 3 дает фильтр высоких частот Чебышева 5-го порядка с пульсацией 1 дБ.
Рис. 5. Эти выходы SPICE моделируют отклик цепей Чебышева верхних и нижних частот.
Заключение
Используя вышеупомянутые методы, вы можете разработать фильтры нижних и верхних частот с откликом на любой частоте. Полосовые и полосовые фильтры также могут быть реализованы (с одним операционным усилителем) с использованием методов, аналогичных показанным, но эти приложения выходят за рамки данной статьи.Однако вы можете реализовать полосовой и полосовой фильтры путем каскадного подключения фильтров нижних и верхних частот. Информацию об операционных усилителях Maxim можно найти в разделе «Усилители и компараторы».
Приложение
Расположение полюсов Баттерворта Заказать Реальный Воображаемое -а ± jb 2 0,7071 0,7071 3 0.5000 0,8660 1,0000 4 0,9239 0,3827 0,3827 0,9239 5 0.8090 0,5878 0,3090 0,9511 1,0000 6 0,9659 0.2588 0,7071 0,7071 0,2588 0,9659 7 0,9010 0,4339 0,6235 0,7818 0,2225 0,9749 1,0000 8 0,9808 0,1951 0.8315 0,5556 0,5556 0,8315 0,1951 0,9808 9 0,9397 0,3420 0,7660 0,6428 0,5000 0,8660 0,1737 0,9848 1.0000 10 0,9877 0,1564 0,8910 0,4540 0,7071 0,7071 Конструкция аналогового фильтра
Скалы и ущелья .. Создание аналогового фильтра нижних частот
Это пятая в серии статей по базовым концепциям сбора цифровых данных. В первом первом блоге мы говорили о том, как разные стратегии сбора данных дают нам разные, но одинаково правильные (или неправильные) результаты.Во второй части мы обсудили основы выборки, алиасинг и непоправимые ошибки, которые они вызывают, а в третьей части мы начали обсуждение того, какие стратегии фильтрации и частоты дискретизации необходимы для уменьшения ошибок наложения имен до «приемлемых» уровни. , четвертый, , охватывает плюсы и минусы типов фильтров, которые мы могли бы использовать для защиты от псевдонимов. Здесь и в следующем мы обсудим концепции оборудования, необходимые для достижения этих целей.
Философия .. Будьте проще
Мы собираемся обсудить стратегии, используемые для разработки полезных аналоговых фильтров нижних частот из базовых строительных блоков. Мы не собираемся уходить далеко в неизведанное, поэтому нам не нужно беспокоиться о стабильности и тому подобном. Надеюсь, это не обидит наших читателей, более склонных к математике.
Итак, давайте создадим несколько фильтров
Как только Шеннон и его соавторы обнаружили основные концепции и проблемы, связанные с измерениями цифровых данных, появились решения проблемы наложения спектров.Были разработаны аналоговые фильтры нижних частот, которые ослабляли энергию выше частоты Найквиста ( F N ) и, следовательно, уменьшали наложение спектров. Позже, когда вычислительные мощности увеличились, к делу присоединились цифровые фильтры.
Итак, приступим к аналоговым фильтрам… В следующий раз мы сделаем гибридный / цифровой ( SD ).
Столбы … Основные строительные блоки
На рисунке 1 показаны принципиальная схема операционного усилителя и передаточная функция однополюсного фильтра.Его особенности / характеристики:
- Его частота среза ( F C , где затухание = 3 дБ, усиление ~ 0,707) и усиление на низких частотах регулируются резисторами и конденсаторами в цепи.
- I скатывается на -6 дБ / октава = -20 дБ / декада (что является причудливым способом сказать, что его высокочастотное затухание прямо пропорционально частоте).
- Фаза (запаздывание) равна нулю на нулевой частоте, проходит через 45 градусов при F C и приближается к 90 градусам на высокой частоте.
Это недостаточно резкий, чтобы быть полезным в качестве фильтра сглаживания. Возможно, мы могли бы соединить их несколько последовательно, чтобы сделать многополюсный фильтр. Результат соединения 4 из них последовательно (что приводит к умножению передаточных функций) показан на рисунке 2.
На высоких частотах он катится в 4 раза быстрее (хорошо), но его затухание (амплитудные искажения) в полосе пропускания (ниже F C ) довольно плохое.Мы можем добиться большего.
Давайте сделаем перерыв, чтобы попросить вас присоединиться к обсуждению.
Если повезет, я вызвал несколько вопросов и / или разногласий в этих блогах.
Например, первый блог вызвал комментарий / вопрос о моем заявлении о том, что мне не нравятся фильтры Бесселя. Думаю, что ответил, что в предыдущая запись . Вы согласны?
Внизу страницы вы найдете способы связаться со мной .Двухполюсная цепь на помощь
К счастью, есть инструмент получше.На рисунке 3 показаны принципиальная схема и передаточные функции нескольких двухполюсных фильтров с разным демпфированием.
Критические характеристики:
- Помимо возможности регулировки частоты среза ( F C ), мы также можем контролировать «пикообразность» ( Q ) передаточной функции. На рисунке показаны амплитудные и фазовые характеристики для различных Qs (0,5, 0,707, 1.0 и 3.0.).
- На частотах значительно выше F C все они спадают на -12 дБ / октаву.
- Фаза начинается с 0 и проходит через 90 градусов при F C на своем пути до 180 градусов с бесконечной частотой. Более высокое значение Qs приводит к более быстрому изменению фазы около F C .
Если мы соединим несколько таких цепей последовательно, мы сможем построить многополюсный фильтр.Например, если бы мы объединили четыре 2-полюсные схемы на рисунке 3 для создания 8-полюсного фильтра, мы получили бы передаточную функцию, показанную на рисунке 4. Его коэффициент затухания на высокой частоте составляет -8 x 6 = -48 дБ / октаву. и он довольно плоский в полосе пропускания (< F C ). Неплохой фильтр нижних частот, но мы можем сделать лучше.
Это основная идея. Добавление большего количества (правильно настроенных) полюсов (и нулей, как мы вскоре увидим) даст более четкий фильтр.На рисунке 5 показан эффект добавления дополнительных полюсов.
Каждый полюс увеличивает крутизну спада на 6 дБ / октаву и обеспечивает большее затухание высоких частот.
Это так просто, или нет?
Как разработать фильтр, отвечающий нашим требованиям? К счастью, здесь нас опередили умные люди.
В 1930 году Стивен Баттерворт разработал семейство наборов фильтров, названных в его честь, а в 1949 году У. Э. Томпсон применил функции Бесселя для управления коэффициентами фильтра для создания набора фильтров « Бесселя » с различными желательными характеристиками.Они стали стандартами в отрасли.
Конструкции 8-полюсных фильтров Бесселя и Баттерворта показаны на рисунке 6.
В левом кадре показаны отдельные передаточные функции четырех двухполюсных каскадов. Частоты и Qs каскадов показаны в нижнем левом углу. В правом кадре показан конечный результат: продукт отдельных каскадов, полученный при последовательном соединении четырех цепей. На вставке в левом нижнем углу показан увеличенный вид полосы пропускания фильтра.
Сравнение двух стратегий показывает:
- Обе конструкции имеют спад на 48 дБ / октаву на высокой частоте
- В конструкции Баттерворта используются каскады на более низкой частоте и с гораздо более высокой добротностью. Это дает более плоскую полосу пропускания и спад на более низкой частоте.
- Комбинация полюсов и нулей в конструкции Бесселя дает постоянную задержку / линейную фазу (см. Обсуждение в четвертом блоге ).
Эти фильтры использовались до 1975 года.
Потом пришли нули
В конце 70-х появился новый вид фильтра, в который вошли «нули». Нуль может быть создан путем инвертирования двухполюсного отклика с нулевым демпфированием для получения передаточной функции, показанной на рисунке 7.
Его основные характеристики:
- Прирост значительно ниже F C составляет 1.
- Прирост составляет ~ 0 при F C
- Крутизна усиления намного выше F C составляет +12 дБ / октаву.Это бесконечно на бесконечной частоте.
- Фазовый сдвиг 180 o на F C .
Здесь нам нужно разобраться с какой-то странной номенклатурой. Для создания такой формы фильтра требуется двухполюсная схема. Значит, засчитывается как два нуля!
Чтобы создать фильтр, нули должны быть объединены с парами полюсов, чтобы уменьшить усиление на высокой частоте. Полезный фильтр должен иметь количество полюсов, равное или большее, чем нулей.
Введите эллиптические фильтры
Фильтры с нулями называются Elliptical.
На рисунке 9 показаны характеристики эллиптического фильтра с 8 полюсами и 8 нулями, который оптимизирован для характеристик подавления псевдонимов. Он был предложен Tustin Electronics ( R.I.P. ) в середине 1980-х годов.
Его основные характеристики:
- Он имеет пульсацию 0,5% P-P в полосе пропускания (пульсации полосы пропускания — характерная черта эллиптических фильтров).
- Он очень быстро скатывается до пика пульсации -84 дБ (15848/1) при F / F C = 1.5. F / F C для затухания 1000/1 составляет 1,41. Согласно правилам, описанным в предыдущем блоге, это позволит минимальное соотношение выборки S / F D = 2,41.
- Фаза выше отсечки действительно тупая (где это не имеет особого значения).
Обратите внимание, что я не указал степень затухания фильтра, потому что это не имеет большого значения. Важнейшей особенностью является соотношение частот, при котором достаточное затухание.
Фильтр Тастина обладает замечательными характеристиками, которые вряд ли можно найти в современных системах. Важнейшей особенностью является пара полюсов с Q> 10. Этого очень сложно добиться по практическим причинам. Эти системы были построены эльфами с помощью крошечных отверток.
Этот фильтр является примером использования нулей для обеспечения «оптимального» отклонения псевдонимов. Использование нулей и полюсов также предлагает возможности для оптимизации других характеристик.Примеры можно найти здесь .
Подробный анализ производительности и полезности всех этих фильтров можно найти в предыдущем блоге .
В следующем блоге будет рассмотрено следующее поколение систем защиты от псевдонимов: фильтры с гибридной передискретизацией и сигма-дельта ( SD ).
Список литературы
Следующие веб-указатели предоставят вам дополнительную информацию и, в некоторых случаях, другой взгляд на операцию фильтрации нижних частот.
https://en.wikipedia.org/wiki/Bessel_filter
https://en.wikipedia.org/wiki/Butterworth_filter
https://en.wikipedia.org/wiki/Elliptic_filter
http://www.analog.com/media/en/training-seminars/design-handbooks/Basic-Linear-Design/Chapter8.pdf
http://www.electronics-tutorials.ws/filter/second-order-filters.html
http://www.pfinc.com/paper_briefs/anti_alias_brief.pdf
http://www.freqdev.com/guide/analog.html
https: // www.maximintegrated.com/en/app-notes/index.mvp/id/733
Отправить комментарий или вопрос на Strether
Одна из причин, по которой я веду эти блоги, состоит в том, чтобы начать обсуждение. Пожалуйста, обращайтесь ко мне с любыми вопросами или комментариями, которые могут у вас возникнуть.
Вы можете принять участие по:
- Ввод комментариев / вопросов ниже в Раздел комментариев в конце блога. Очевидно, это будет доступно всем читателям.
- Свяжитесь со мной напрямую. Я отвечу конфиденциально и (надеюсь) быстро. Если возможно, ваш вопрос может стать темой будущего блога.
Этот блог предназначен для семинара … не для лекции. Мне нужна ваша помощь и отзывы, чтобы все было хорошо!
Заявление об ограничении ответственности
Strether не имеет официального отношения к Mide или enDAQ, линейке продуктов Mide, и не поддерживает продукцию Mide или любого другого поставщика, если это явно не обсуждается в его сообщениях в блоге.
Дополнительные ресурсы
Если вы хотите узнать немного больше о различных аспектах испытаний и анализа на удар и вибрацию, загрузите нашу бесплатную электронную книгу «Обзор испытаний на удар и вибрацию». Там есть несколько примеров, предыстория и множество ссылок, по которым вы можете узнать больше. И, как всегда, не стесняйтесь обращаться к нам, если у вас есть какие-либо вопросы!
Проектирование банков цифровых фильтров с использованием вейвлетов | Журнал EURASIP о достижениях в обработке сигналов
1. А. Амбеде, К.Г. Смита, А.П. Винод, Гибкие универсальные и неоднородные блоки цифровых фильтров низкой сложности с высоким частотным разрешением для многостандартных радиостанций. IEEE Trans. Система очень крупномасштабной интеграции (СБИС). 23 (4), 631–641 (2015)
Статья
Google Scholar
2. З. Фанг, С. Пенгланг, Построение блоков фильтров с неоднородной модуляцией DFT посредством фазовой модуляции. J. Electron. Инф. Technol. 39 (3), 2169–2174 (2017)
Google Scholar
3. J.Z. Цзян, Ф. Чжоу, П.Л. Шуй, Разработка двухканального банка фильтров биортогонального графа на основе лифтинга. Сигнальный процесс IET. 10 (6), 670–675 (2016)
Статья
Google Scholar
4. J.Z. Цзян, Ф. Чжоу, П.Л. Шуй, С. Оуян, Теория и разработка двумерного модуля фильтров DFT с произвольными матрицами модуляции и децимации. Цифра. Сигнальный процесс. 44 , 123–130 (2015)
MathSciNet
СтатьяGoogle Scholar
5. D.B.H. Тай, З. Лин, Дизайн банков фильтров почти ортогональных графов. Сигнальный процесс IEEE. Lett. 22 (6), 701–704 (2015)
Статья
Google Scholar
6. F. Zhou, P.L. Шуй, Дж. З. Цзян, Дизайн двухмерных модифицированных блоков фильтров с модуляцией DFT на основе метода множителя Лагранжа. J. Electron. Инф. Technol. 39 (5), 1261–1265 (2017)
Google Scholar
7. Ю.С. Вон, К.У. Bae, N.H. Myung, Метод проектирования полосового фильтра с усиленным подавлением полосы задерживания с использованием спиральных SIR. Электрон. Lett. 48 (17), 1067–1068 (2012)
Артикул
Google Scholar
8. И. Добеши, Ортонормированные базисы всплесков с компактным носителем. Commun. Pure Appl. Математика. 41 , 909–996 (1988)
MathSciNet
СтатьяGoogle Scholar
9. Дж. Шен, Г. Странг, Нули многочленов Добеши. Proc. Являюсь. Математика. Soc. 124 (12), 3819–3833 (1996)
Артикул
Google Scholar
10. К. Вонеш, Т. Блю, М. Унсер, Обобщенные семейства вейвлетов Добеши. IEEE Trans. Сигнальный процесс. 55 (9), 4415–4429 (2007)
MathSciNet
СтатьяGoogle Scholar
11. г.Strang, Создание и сравнение вейвлетов (Техническая статья, Департамент математики, Массачусетский технологический институт, Кембридж, 1994), стр. 1–10
MATH
Google Scholar
12. К. Тасвелл, Семейства вейвлет-фильтров Добеши, выбранных по ограничению и оптимизированные для поиска, вычисляемые с помощью спектральной факторизации (Технический документ, Computational Toolsmiths, Stanford, 2000)
Книга
Google Scholar
13. М. Оиси, С. Моро, Т. Мацумото, Модифицированный метод анализа цепей с использованием вейвлет-преобразования Хаара с адаптивным разрешением — для цепей с формой волны с резкими выпуклыми диапазонами. Европейская конф. Теория схем (ECCTD) 1 (1), 299–302 (2009)
Google Scholar
14. М. Оиси, С. Моро, Т. Мацумото, Точность метода анализа цепей с использованием вейвлет-преобразования с адаптивным разрешением. Конференция IEEE Region 10 (TENCON) 1 (1), 1177–1181 (2010)
Google Scholar
15. Х.М. Се, С.С.Чан, Т.И. Юк, Разработка банков неравномерных рекомбинационных фильтров с идеальной реконструкцией и гибкими рациональными коэффициентами дискретизации. IEEE Trans. Circuits Syst. I — Обычные документы 52 (9), 1965–1981 (2005)
Статья
Google Scholar
16. Л. Фанг, В. Чжун, К. Чжан, Разработка M-канальных линейно-фазовых неоднородных фильтров с произвольными рациональными коэффициентами дискретизации. Сигнальный процесс IET. 10 (2), 106–114 (2016)
Статья
Google Scholar
17. W. Zhang, Y. Chen, Z. Dou, J. Hu, Низкая сложность и узкополосные блоки фильтров для программно определяемых радиоприложений (13-я Международная конференция IEEE по обработке сигналов (ICSP), Чэнду, 2016), стр. 1171–1175
Google Scholar
18. Б. Боашаш (ред.), Частотно-временной анализ и обработка сигналов — исчерпывающий справочник , 2-е изд. (Academic Press, Нью-Йорк, 2015)
Google Scholar
19. П.П. Вайдьянатан, Банки фильтров в цифровых коммуникациях. IEEE Circuits Syst. Mag. 1 (2), 4–25 (2001)
Google Scholar
20. X. Chen, F.J. Harris, E. Venosa, B.D. Rao, Банки фильтров анализа / синтеза без максимального прореживания: приложения для широкополосной цифровой фильтрации. IEEE Trans. Сигнальный процесс. 62 (4), 852–867 (2014)
MathSciNet
СтатьяGoogle Scholar
21. Маллат С.Г. Теория разложения сигналов с разным разрешением: вейвлет-представление. IEEE Trans. Pattern Anal. Мах. Интеллект. 11 (7), 674–693 (1989)
Статья
Google Scholar
22. И. Добеши, Десять лекций по вейвлетам, Региональная конференция CBMS-NSF. Серия в Прил. Математика (SIAM) 61, Филадельфия, Пенсильвания, 1992
23. А. Салазар и др., Автоматическое обнаружение мошенничества с кредитными картами на основе нелинейной обработки сигналов.IEEE Int. Carnahan Conf. Security Technol. (ICCST) 1 (1), 207–212 (2012)
Google Scholar
24. К. Пурвуайер, Р. Хейджер, Безопасное использование ADS-B в слежении за УВД. Tyrrhenian Int. Цифра мастерской. Commun. Расширенный обзор. Самолеты (TIWDC / ESAV) 1 (1), 35–40 (2014)
Google Scholar
25. Р. Парсех, К. Кансанен, Эффекты разнесения в оценке гаусс-марковского процесса по каналу с замираниями.IEEE Int. Конф. Commun. (ICC) 1 (1), 4644–4649 (2014)
MATH
Google Scholar
26. К. Сунг-Ын и др., Передача звука через человеческое тело с помощью метода цифровой модуляции Уивера (DWM). Аня. IEEE Syst. Конференция (SysCon) 1 (1), 176–179 (2014)
Google Scholar
27. М. Веттерли, К. Херли, Вейвлеты и банки фильтров: теория и дизайн.IEEE Trans. Сигнальный процесс. 40 (9), 2207–2232 (1992)
Артикул
Google Scholar
28. E.S. Филатова, Д. Филатов, А.Д. Стоцкая, Г. Дубровский, Модель представления динамики энергопотребления в системе прогнозирования электрической нагрузки. IEEE NW Россия Молодые исследователи Электрическая электроника. Англ. Конференция (EIConRusNW) 1 (1), 175–179 (2015)
Статья
Google Scholar
29. С.Н. Mate, Идентификация изменяющейся во времени системы с использованием подхода на основе вейвлетов с использованием нескольких базисных функций вейвлетов. 2-й Int. Конференция Электрон. Commun. Syst. (ICECS) 1 (1), 441–446 (2015)
Google Scholar
30. N.W.A. Lidula, R.M.M.P. Нишшанка, С. Wijesundara, W.L.K.D. Виджеманна, W.N.L. Weerakkody, Разработка тестовой системы микросетей для анализа переходных процессов. Moratuwa Eng. Res. Конференция (MERCon) 1 (1), 88–93 (2015)
Статья
Google Scholar
31. А. Коэн, И. Добеши, Б. Джаверт, П. Виал, Вейвлеты многомасштабного анализа и быстрые алгоритмы на интервале. C. R. Acad. Sci. Париж, сер. i Math 316 , 417–421 (1992)
MathSciNet
МАТЕМАТИКАGoogle Scholar
32. А.Н. Акансу, Р.А. Haddad, Разложение сигналов с несколькими разрешениями — преобразования, поддиапазоны и вейвлеты , 2-е изд. (Academic Press, 2001)
33. Х. Янгми, П.Хёнджу, З. Фанг, Разработка банка многоуровневых вейвлет-фильтров с использованием теоремы Квиллена-Суслина для полиномов Лорана. IEEE Trans. Сигнальный процесс. 62 (20), 5348–5358 (2014)
MathSciNet
СтатьяGoogle Scholar
34. A.I. Маркушевич, Теория функций комплексного переменного , 2-е изд. (AMS Chelsea Publishing, Нью-Йорк, 2011 г.)
Google Scholar
35. J.D. Certic, Эффективные структуры цифровых фильтров на основе секций всепроходных фильтров, Телекоммуникационный форум (TELFOR) , 19-е изд. (2011), стр. 743–750
Google Scholar
36. Л. Цзянь-ао, многомерные блоки PR-фильтров с FIR-фильтрами. Int. Конф. Commun. Circuits Syst. Proc. 1 , 162–166 (2006)
Google Scholar
37. К. Авчи и Э.Гюмюссой, Проектирование банков косинусно-модулированных M-каналов на основе экспоненциального окна, 24-я Конференция по обработке сигналов и передаче данных (SIU), Зонгулдак, 845–848, 2016 г.
38. С. Дхабу, В.А. Прасад, Разработка модифицированных частотных преобразований второго порядка на основе переменных цифровых фильтров с большим диапазоном частот среза и улучшенными характеристиками переходной полосы. IEEE Trans. Система очень крупномасштабной интеграции (СБИС). 24 (2), 413–420 (2016)
Статья
Google Scholar
39. З. Сонгбай, З. Лей, Общий метод синтеза симметричного полосового фильтра Чебышева четного порядка. Микроволновая конф. Proc. (APMC) 1 (1), 667–669 (2012)
Google Scholar
40. Р. Шауманн, Х. Сяо, М.Э. Ван Валкенбург, Разработка аналоговых фильтров , 2-е изд. (Oxford University Press, США, 2009)
Google Scholar
41. Д. Вэй, А.В. Оппенгейм. Алгоритмы линейного программирования для проектирования разреженных фильтров. IEEE Trans. Сигнальный процесс. 58 (3), 1605–1617 (2010)
MathSciNet
СтатьяGoogle Scholar
42. Д. Вэй, А.В. Оппенгейм, алгоритм ветвей и границ для проектирования разреженных фильтров с квадратичными ограничениями. IEEE Trans. Сигнальный процесс. 61 (4), 1006–1018 (2013)
Артикул
Google Scholar
43. С. Прити, М.Дж. Шила, Эффективная по площади конструкция фильтра верхних и нижних частот для приложений DWT. Int. Конф. Электрон. Commun. Syst. (ICECS) 1 , 1–5 (2014)
Google Scholar
44. F. Ramirez-Echeverria, A. Sarr, Y.S. Шмалий, Оптимальная память для дискретных КИХ-фильтров в пространстве состояний. IEEE Trans. Сигнальный процесс. 62 , 557–561 (2014)
MathSciNet
СтатьяGoogle Scholar
45. Ф. Дин, Ю. Ван, Дж. Дин, Рекурсивные алгоритмы определения параметров наименьших квадратов для систем с цветным шумом с использованием техники фильтрации и вспомогательной модели. IEEE Trans. Цифровой сигнальный процесс. 37 , 100–108 (2015)
Статья
Google Scholar
46. Й. Лю, Ф. Дин, Й. Ши, Эффективный метод иерархической идентификации для общих двухскоростных систем дискретизации данных. Automatica 50 , 962–970 (2014)
MathSciNet
СтатьяGoogle Scholar
47. А. Аггарвал, М. Кумар, Т.К. Рават и др., Оптимальный дизайн двумерных КИХ-фильтров с квадрантно-симметричными свойствами с использованием ограничений дробной производной. Circuits Syst. Сигнальный процесс. 35 (6), 2213–2257 (2016)
Статья
Google Scholar
48. Н. Рашми, Г. Бегум, В. Сингх, Удаление шума ЭКГ с использованием вейвлет-преобразования и фильтров (Международная конференция по беспроводной связи, обработке сигналов и сети (WiSPNET), Ченнаи, 2017), стр.2395–2400
Google Scholar
49. М. Шарма, П.В. Ахут, Р.Б. Пачори, В. Гадре, Метод параметризации для разработки совместных частотно-временных оптимизированных баз биортогональных вейвлетов с дискретным временем. Signal Process., 107–120 (2017)
Статья.

 С. 32.
С. 32.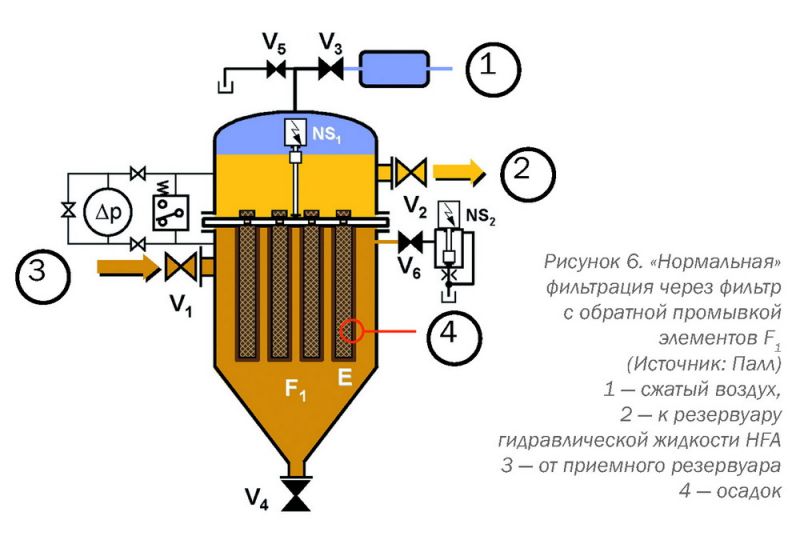 43rd Annual Symp. Freq. Control, 1989, p.596-605
43rd Annual Symp. Freq. Control, 1989, p.596-605 В. Исследование и разработка физических методов проектирования высокоизбирательных акустоэлектронных приборов с малым вносимым затуханием диссертация на соискание ученой степени кандидата технических наук автореферат диссертации на соискание ученой степени кандидата технических наук / Москва, 2003/
В. Исследование и разработка физических методов проектирования высокоизбирательных акустоэлектронных приборов с малым вносимым затуханием диссертация на соискание ученой степени кандидата технических наук автореферат диссертации на соискание ученой степени кандидата технических наук / Москва, 2003/ 7 См/м.
7 См/м.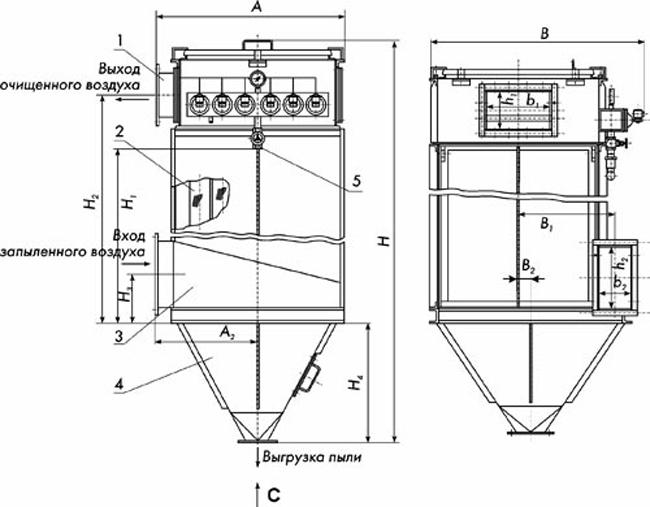 47 / 8.40
47 / 8.40