В чем измеряется си путь измеряется в: Какая единица измерения в СИ является основной для измерения пути? А)сантиметр Б)метр
Содержание
Единицы измерения расстояний и редактирование—Справка
При редактировании единицы карты для фрейма данных используются при получении и вводе измерений и расстояний. Единицами карты называются единицы, используемые для отображения пространственных данных во фрейме данных. Единицы карты определяются системой координат фрейма данных. При редактировании все значения, которые вы вводите, по умолчанию будут считаться введенными в единицах карты. Вы можете посмотреть, какие единицы используются системой координат, если зайдёте в диалоговое окно Свойства фрейма данных (Data Frame Properties) на закладку Общие (General).
Иногда при создании объектов необходимо ввести значения, которые записаны в других единицах измерения, отличных от единиц карты. Когда вы вводите измерения, в ряде случаев возможен ввод значения в единицах измерения, отличных от единиц карты, с помощью добавления аббревиатур единиц измерения.
Например, представьте, что данные имеют систему координат State Plane и линейными единицами измерения являются футы. Вы получили измерения в метрах. Вместо преобразования измерений в футы, вы можете указать аббревиатуру для метров, m, после значения измерения и инструменты корректно преобразуют это расстояние.
Вы получили измерения в метрах. Вместо преобразования измерений в футы, вы можете указать аббревиатуру для метров, m, после значения измерения и инструменты корректно преобразуют это расстояние.
Когда требуется ввести расстояние в инструменты редактирования, то всегда есть возможность указать единицы измерения и ввести число, которое будет преобразовано в единицы карты. Аббревиатуры единиц измерения работают только при использовании системы координат проекции, а не географической системы координат для фрейма данных.
Следующие секции описывают основные сокращения, которые поддерживаются для ввода при редактировании, а также их применение.
Метрические единицы
| Единицы расстояния | Аббревиатура | Метров в единице | Описание |
|---|---|---|---|
Километр | Км | 1,000 | 1000 метров |
Метр | М | 1 | Международная единица |
Сантиметр | См | . | Ровно 1/100 метра |
Миллиметр | Мм | 0.001 | 1/1000 метра |
Метрические единицы
Британские единицы
| Единицы расстояния | Аббревиатура | Метров в единице | Описание |
|---|---|---|---|
Фут | Фт | 0.3048 | Стандартные футы используются в США. Также назывался британским футом и использовался во многих странах до введения метрической системы измерений. |
Миля | Мл | 1,609. | Также определяемая как стандартная миля, равная 5,280 стандартных футов. |
Морская миля | Нм | 1,852 | Морская миля — это единица измерения расстояний, используемая в основном в навигации на море и в авиации. Морская миля определяется как среднее расстояние на земной поверхности в одной минуте широты. В 1929 году морская миля была точно определена как 1852 метра или 6,076.11549 футов, эта единица расстояния известна как международная морская миля. |
Чейн | Ch | 20.1168 | 66 международных футов. |
Ярд | Yd | 0. | 3 международных фута. |
Род | Rd | 5.0292 | 1/4 чейна, или 16.5 футов. |
Линк | Lk | 0.201168 | 1/100 чейна или 66/100 фута. |
Дюйм | Д (in) | 0.0254 | 1/12 международного фута. |
Британские единицы
Геодезические единицы измерений США
| Единицы расстояния | Аббревиатура | Метров в единице | Описание |
|---|---|---|---|
Геодезический фут | ftUS | 0. | Геодезические футы используются в Государственной системе координат США. В США фундаментальные геодезические единицы, такие как род, чейн, миля, акр, секция и округ связаны с геодезическим футом. Точный перевод американского геодезического фута в метры может быть выполнен путём умножения на дробь 1,200/3,937. |
Геодезическая миля | miUS | 1,609.3472186944 | 5,280 геодезических футов. |
Геодезический чейн | chUS | 20.1168402337 | 66 геодезических футов. |
Геодезический род | rdUS | 5. | 1/4 геодезического чейна. |
Геодезический линк | lkUS | 0.2011684023 | 1/100 геодезического чейна. |
Геодезический ярд | ydUS | 0.9144018288 | 3 геодезических фута. |
Геодезические единицы измерений США
Ввод определенных местоположений (DD, DMS, DDM, MGRS, USNG и UTM)
В командах редактирования, которые требуют ввода определенных местоположений, вы можете указывать местоположения с помощью пары координат широта/долгота, местоположения в системе грид координат Military Grid Reference System (MGRS), местоположение в системе координат U.S. National Grid (USNG) или с помощью координат в системе координат UTM. По умолчанию единицами измерения являются единицы карты, но вы можете нажать кнопку Единицы чтобы выбрать единицы для ввода координат.
По умолчанию единицами измерения являются единицы карты, но вы можете нажать кнопку Единицы чтобы выбрать единицы для ввода координат.
Это те же форматы, которые используются в команде Перейти к точке XY (Go To XY). Ниже приведены указания для ввода таких значений. Их можно использовать для команды Абсолютные XY (Absolute XY) и таких команд, как Переместить в, которые позволяют перемещать вершины или элементы топологии в заданную точку.
- Помните, что x — это значение долготы (Восточной/Западной), а y — значение широты (Северной/Южной), они указываются именно в таком порядке. Сферические координаты не всегда указываются в таком же порядке, поэтому убедитесь, что в диалоговом окне вы сначала ввели значение долготы. Например, если вам даны значения 17.1325, -60.666, нужно уточнить какое из этих значений является широтой, а какое долготой. Наиболее удобным способом однозначного задания координат является указание полушария с помощью букв В, З, С, Ю (E, W, N, S).
- Если вы работаете в форматах Десятичные градусы (DD), Градусы Минуты Секунды (DMS) или Градусы, десятичные минуты (DM), значения координат можно внести с отрицательным знаком, если точка находится в западном или южном полушарии, или добавить символы E, W, N, S.

- Значения координат в форматах DMS или DM можно разделять пробелами или специальными символами °, ‘, » (удобно, когда вы копируете значения координат из других диалоговых окон или приложений), можно сочетать оба способа.
- Независимо от того, какой формат координат (DD, DMS или DM) вы используете, значения можно ввести в любом из них, после чего они автоматически конвертируются в выбранный.
- Если вы работаете с форматами DD и DM, то введенные значения координат всегда конвертируются в строки с отрицательными значениями для западного и южного полушарий.
- Если вы используете формат DMS, то введенные координат конвертируются в строки с буквами E, W, N, S для определения полушария, а также со специальными символами °, ‘, «.
- При использовании систем координат MGRS или USNG, убедитесь, что в строке координат нет пробелов.
Примеры корректного ввода координат в виде долгота-широта
-45 | -45 |
45 W | 45 S |
45. | 45.50S |
W45 | S45 |
45 30.5W | 44 30.5S |
45° 30’30″W | 45°30’30″N |
45 30 30 W | 45 30 30 N |
-45 30 30 | 45 30 30 |
45 30.50W | 45 30.50 |
-45.50833 | 45.50833 |
Примеры корректного ввода координат в форматах MGRS и USNG
18SUH | 100,000-метровый квадрат | 0-разрядная координата |
18SUH64 | 10,000-метровый квадрат | 2-разрядная координата |
18SUH6743 | 1,000-метровый квадрат | 4-разрядная координата |
18SUH678432 | 100-метровый квадрат | 6-разрядная координата |
18SUH67894321 | 10-метровый квадрат | 8-разрядная координата |
18SUH6789043210 | 1-метровый квадрат | 10-разрядная координата |
Примеры корректного ввода координат в формате UTM
17R 419230 2714967 | 1-метровый квадрат | 13-разрядная координата |
Коэффициенты конвертации
Для конвертации из одной системы измерений в другую используются специальные коэффициенты пересчёта.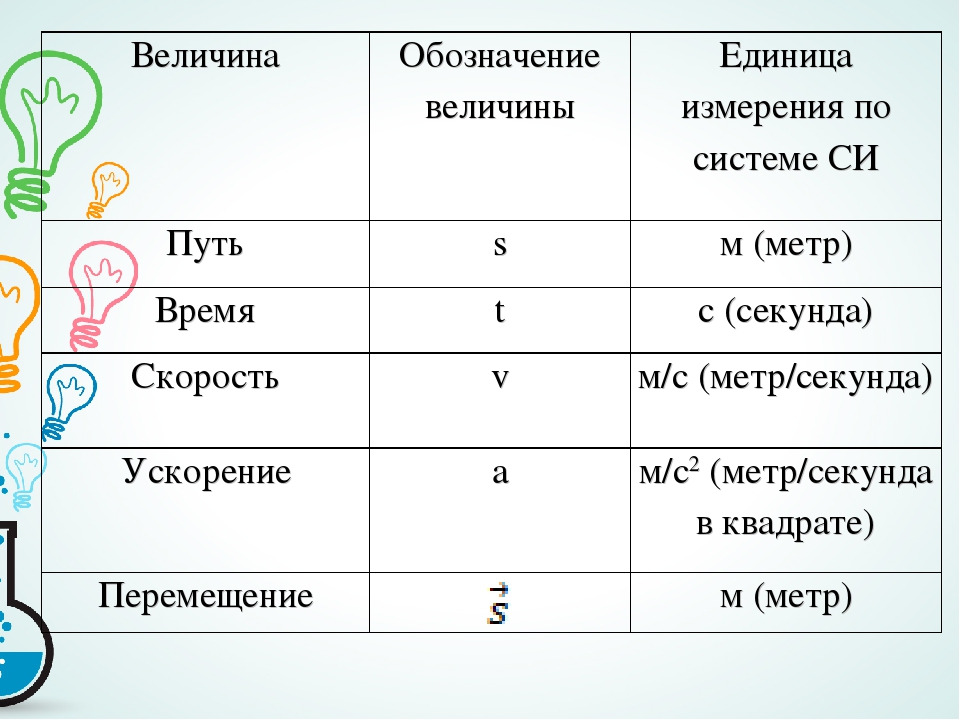 Для конвертации значений из одной системы единиц измерения в другую следует использовать соответствующие коэффициенты пересчёта. Например, чтобы пересчитать футы в сантиметры, надо умножить футы на число 30,48 (27 футов x 30,48 = 822,96 сантиметров). Их список содержится в PDF файле коэффициентов пересчета.
Для конвертации значений из одной системы единиц измерения в другую следует использовать соответствующие коэффициенты пересчёта. Например, чтобы пересчитать футы в сантиметры, надо умножить футы на число 30,48 (27 футов x 30,48 = 822,96 сантиметров). Их список содержится в PDF файле коэффициентов пересчета.
Если ссылка не работает, то можно открыть файл conversion_constants.pdf из папки \Documentation в директории установки ArcGIS. Для просмотра этого документа нужна программа Adobe Reader.
О геодезических футах США
В 1959 году Национальное Бюро стандартов и Служба береговой и геодезической съёмки США решили переопределить отношение дюйм-сантиметр. Решили, что один дюйм равен ровно 2,54 сантиметрам, а один фут — ровно 0,3048 метрам. Однако в данном соглашении оговаривается, что более старое значение 39,37 дюймов в одном метре будет относиться к геодезическим футам США (U.S. survey foot).
Одной из причин этой оговорки является то, что государственные системы координат, которые созданы на основе национальной геодезической сети, основываются на отношении метра к дюйму в соотношении 1 к 39,37.
Разница между этими двумя значениями одного фута невелика, две миллионных, однако она всё же влияет на точность измерений. Основные объекты геодезической съёмки — роды, чейны, акры, статутные мили, округа и районы — все привязаны к соотношению 39,37 дюймов в одном метре.
Таблица геодезических футов США представляет исправленные значения (геодезические значения) с помощью таблицы преобразования с коэффициентом 39,37.
Связанные темы
Отзыв по этому разделу?
Единицы измерения
Этот урок не будет новым для новичков. Все мы слышали со школы такие понятия как сантиметр, метр, километр. А когда речь заходила о массе, обычно говорили грамм, килограмм, тонна.
Сантиметры, метры и километры; граммы, килограммы и тонны носят одно общее название — единицы измерения физических величин.
В данном уроке мы рассмотрим наиболее популярные единицы измерения, но не будем сильно углубляться в эту тему, поскольку единицы измерения уходят в область физики. Сегодня мы вынуждены изучить часть физики, поскольку нам это необходимо для дальнейшего изучения математики.
Сегодня мы вынуждены изучить часть физики, поскольку нам это необходимо для дальнейшего изучения математики.
Единицы измерения длины
Для измерения длины предназначены следующие единицы измерения:
- миллиметры;
- сантиметры;
- дециметры;
- метры;
- километры.
Самая маленькая единица измерения это миллиметр (мм). Миллиметры можно увидеть даже воочию, если взять линейку, которой мы пользовались в школе каждый день
Подряд идущие друг за другом маленькие линии это и есть миллиметры. Точнее, расстояние между этими линиями равно одному миллиметру (1 мм):
Следующая единица измерения это сантиметр (см). На линейке каждый сантиметр обозначен числом. К примеру наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке выделен числом 15.
В одном сантиметре 10 миллиметров. Между одним сантиметром и десятью миллиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 см = 10 мм
Вы можете сами убедиться в этом, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.
Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.
Следующая единица измерения длины это дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 дм = 10 см
Вы можете убедиться в этом, если посчитаете количество сантиметров на следующем рисунке:
Вы обнаружите, что количество сантиметров равно 10.
Следующая единица измерения это метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 м = 10 дм
К сожалению, метр нельзя проиллюстрировать на рисунке, потому что он достаточно великоват. Если вы хотите увидеть метр в живую, возьмите рулетку. Она есть у каждого в доме. На рулетке один метр будет обозначен как 100 см. Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:
Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:
1 м = 10 дм = 100 см
100 получается путём перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдём к следующей единице измерения длины, которая называется километр.
Километр считается самой большой единицей измерения длины. Есть конечно и другие более старшие единицы, такие как мегаметр, гигаметр тераметр, но мы не будем их рассматривать, поскольку для дальнейшего изучения математики нам достаточно и километра.
В одном километре тысяча метров. Между одним километром и тысячью метрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:
1 км = 1000 м
В километрах измеряются расстояния между городами и странами. К примеру, расстояние от Москвы до Санкт-Петербурга около 714 километров.
Международная система единиц СИ
Международная система единиц СИ — это некоторый набор общепринятых физических величин.
Основное предназначение международной системы единиц СИ — достижение договоренностей между странами.
Мы знаем, что языки и традиции стран мира различны. С этим ничего не поделать. Но законы математики и физики одинаково работают везде. Если в одной стране «дважды два будет четыре», то и в другой стране «дважды два будет четыре».
Основная проблема заключалась в том, что для каждой физической величины существует несколько единиц измерения. К примеру, мы сейчас узнали, что для измерения длины существуют миллиметры, сантиметры, дециметры, метры и километры. Если несколько ученых, говорящих на разных языках, соберутся в одном месте для решения какой-нибудь задачи, то такое большое многообразие единиц измерения длины может породить между этими учеными противоречия.
Один ученый будет заявлять, что в их стране длина измеряется в метрах. Второй может сказать, что в их стране длина измеряется в километрах. Третий может предложить свою единицу измерения.
Поэтому была создана международная система единиц СИ. СИ это аббревиатура от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ).
СИ это аббревиатура от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ).
В СИ приведены наиболее популярные физические величины и для каждой из них определена своя общепринятая единица измерения. К примеру, во всех странах при решении задач условились, что длину будут измерять в метрах. Поэтому, при решении задач, если длина дана в другой единице измерения (например, в километрах), то её обязательно нужно перевести в метры. О том, как переводить одну единицу измерения в другую, мы поговорим немного позже. А пока нарисуем свою международную систему единиц СИ.
Наш рисунок будет представлять собой таблицу физических величин. Каждую изученную физическую величину мы будем включать в нашу таблицу и указывать ту единицу измерения, которая принята во всех странах. Сейчас мы изучили единицы измерения длины и узнали, что в системе СИ для измерения длины определены метры. Значит наша таблица будет выглядеть так:
Единицы измерения массы
Масса – это величина, обозначающая количество вещества в теле.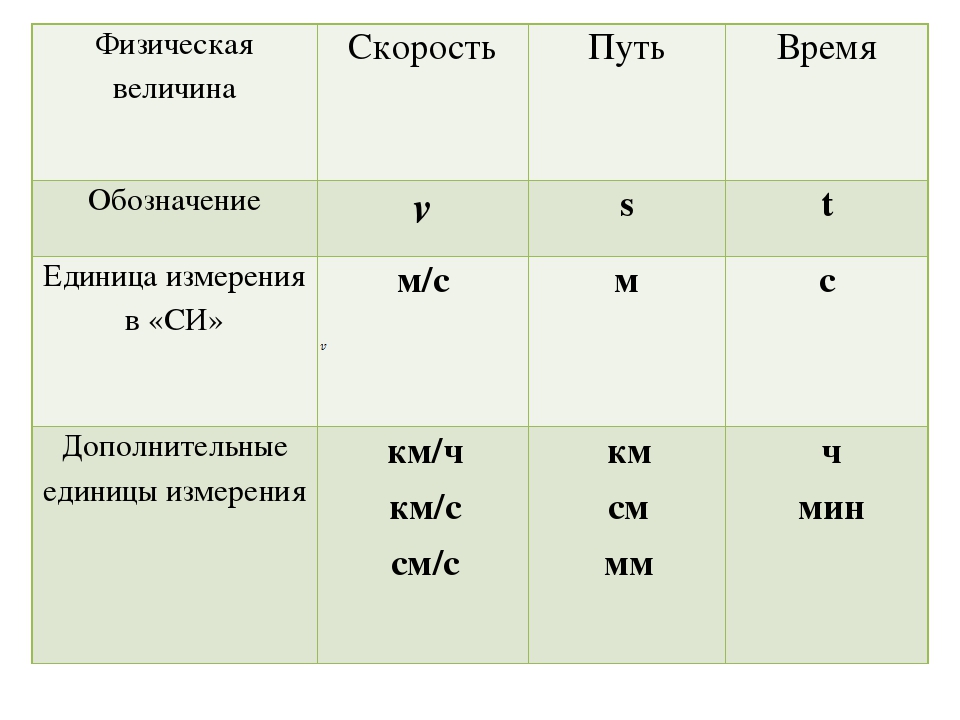 В народе массу тела называют весом. Обычно, когда что-либо взвешивают, говорят «это весит столько-то килограмм», хотя речь идёт не о весе, а о массе этого тела.
В народе массу тела называют весом. Обычно, когда что-либо взвешивают, говорят «это весит столько-то килограмм», хотя речь идёт не о весе, а о массе этого тела.
Вместе с тем, масса и вес это разные понятия. Вес — это сила с которой тело действует на горизонтальную опору. Вес измеряется в ньютонах. А масса это величина, показывающая количество вещества в этом теле.
Но ничего страшного нет в том, если вы назовёте массу тела весом. Даже в медицине говорят «вес человека», хотя речь идёт о массе человека. Главное быть в курсе, что это разные понятия
Для измерения массы используются следующие единицы измерения:
- миллиграммы;
- граммы;
- килограммы;
- центнеры;
- тонны.
Самая маленькая единица измерения это миллиграмм (мг). Миллиграмм скорее всего вы никогда не примените на практике. Их применяют химики и другие ученые, которые работают с мелкими веществами. Для вас достаточно знать, что такая единица измерения массы существует.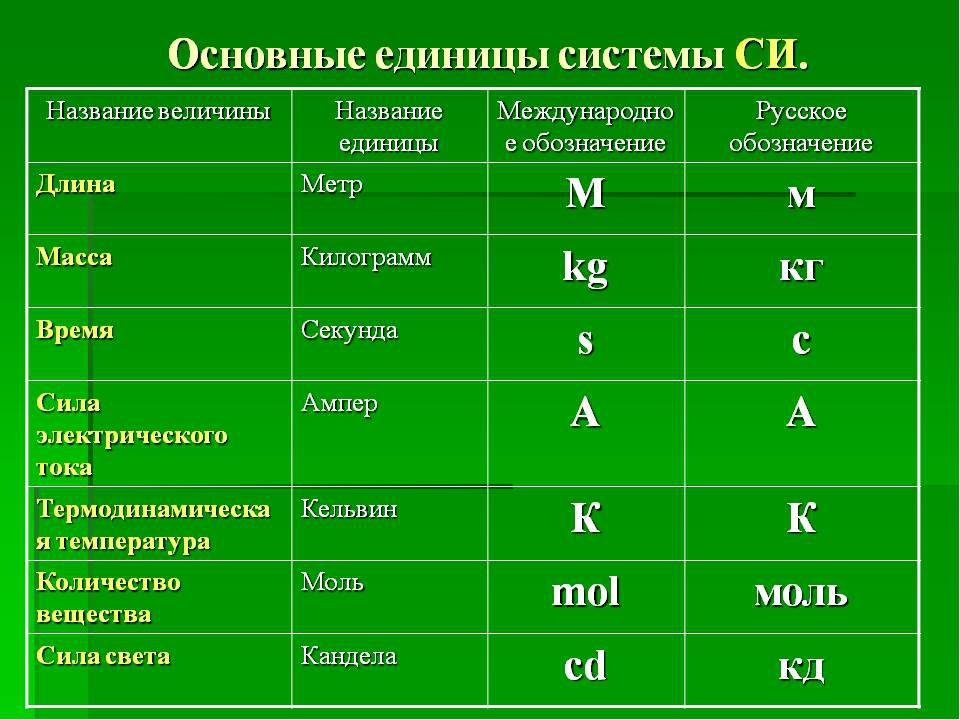
Следующая единица измерения это грамм (г). В граммах принято измерять количество того или иного продукта при составлении рецепта.
В одном грамме тысяча миллиграммов. Между одним граммом и тысячью миллиграммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:
1 г = 1000 мг
Следующая единица измерения это килограмм (кг). Килограмм это общепринятая единица измерения. В ней измеряется всё что угодно. Килограмм включен в систему СИ. Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «масса»:
В одном килограмме тысяча граммов. Между одним килограммом и тысячью граммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:
1 кг = 1000 г
Следующая единица измерения это центнер (ц). В центнерах удобно измерять массу урожая, собранного с небольшого участка или массу какого-нибудь груза.
В одном центнере сто килограммов. Между одним центнером и ста килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:
1 ц = 100 кг
Следующая единица измерения это тонна (т). В тоннах обычно измеряются большие грузы и массы больших тел. Например, масса космического корабля или автомобиля.
В одной тонне тысяча килограмм. Между одной тонной и тысячью килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:
1 т = 1000 кг
Единицы измерения времени
Что такое время думаем объяснять не нужно. Каждый знает что из себя представляет время и зачем оно нужно. Если мы откроем дискуссию на то, что такое время и попытаемся дать ему определение, то начнем углубляться в философию, а это нам сейчас не нужно. Лучше начнём с единиц измерения времени.
Для измерения времени предназначены следующие единицы измерения:
- секунды;
- минуты;
- часы;
- сутки.

Самая маленькая единица измерения это секунда (с). Есть конечно и более маленькие единицы такие как миллисекунды, микросекунды, наносекунды, но их мы рассматривать не будем, поскольку на данный момент в этом нет смысла.
В секундах измеряются различные показатели. Например, за сколько секунд спортсмен пробежит 100 метров. Секунда включена в международную систему единиц СИ для измерения времени и обозначается как «с». Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «время»:
Следующая единица измерения времени это минута (м). В одной минуте 60 секунд. Между одной минутой и шестьюдесятью секундами можно поставить знак равенства, поскольку они обозначают одно и то же время:
1 м = 60 с
Следующая единица измерения это час (ч). В одном часе 60 минут. Между одним часом и шестьюдесятью минутами можно поставить знак равенства, поскольку они обозначают одно и то же время:
1 ч = 60 м
К примеру, если мы изучали этот урок один час и нас спросят сколько времени мы потратили на его изучение, мы можем ответить двумя способами: «мы изучали урок один час» или так «мы изучали урок шестьдесят минут».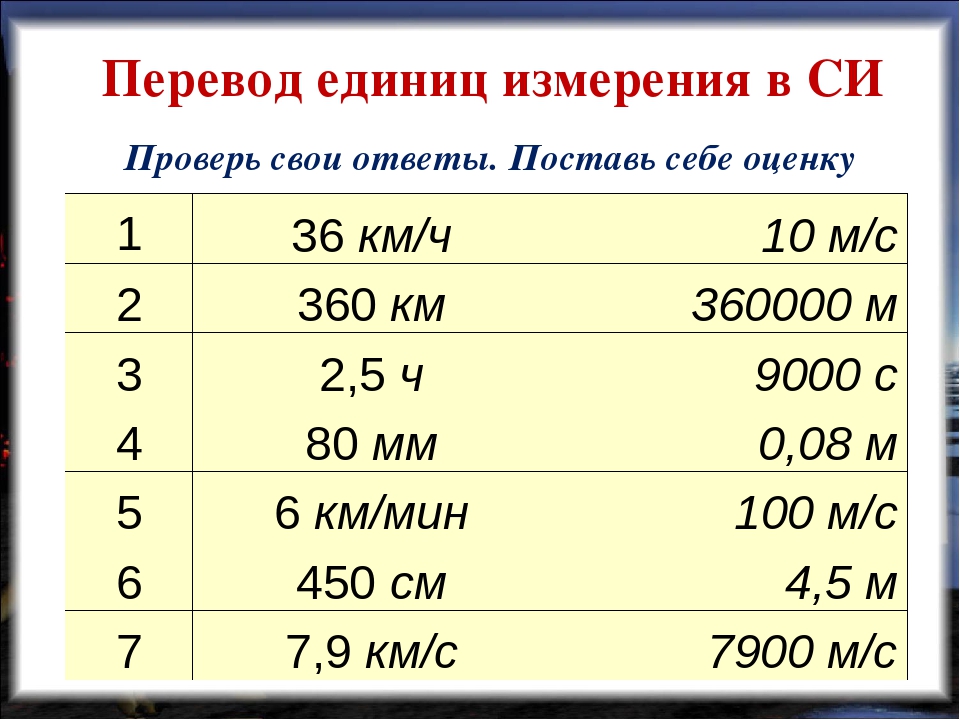 В обоих случаях, мы ответим правильно.
В обоих случаях, мы ответим правильно.
Следующая единица измерения времени это сутки. В сутках 24 часа. Между одними сутками и двадцатью четырьмя часами можно поставить знак равенства, поскольку они обозначают одно и то же время:
1 сут = 24 ч
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
| Параметр | ИСД-5 Стандарт | Примечания |
|---|---|---|
| Диапазон измеряемых скоростей, м/с | 0,01 – 50 | Типичные значения. Чем меньше рабочее расстояние до объекта, тем меньше минимальные и максимальные измеряемые скорости. |
| Точность измеряемой скорости (стандартное отклонение)*, % | ±0,07 ±0,02 | Без усреднения С усреднением 0,2 — 0,3 с, при V > 1 м/с |
| Абсолютная точность измеряемой длины*, % | <±0,05 | При предварительной калибровке на длинах пути >2 м.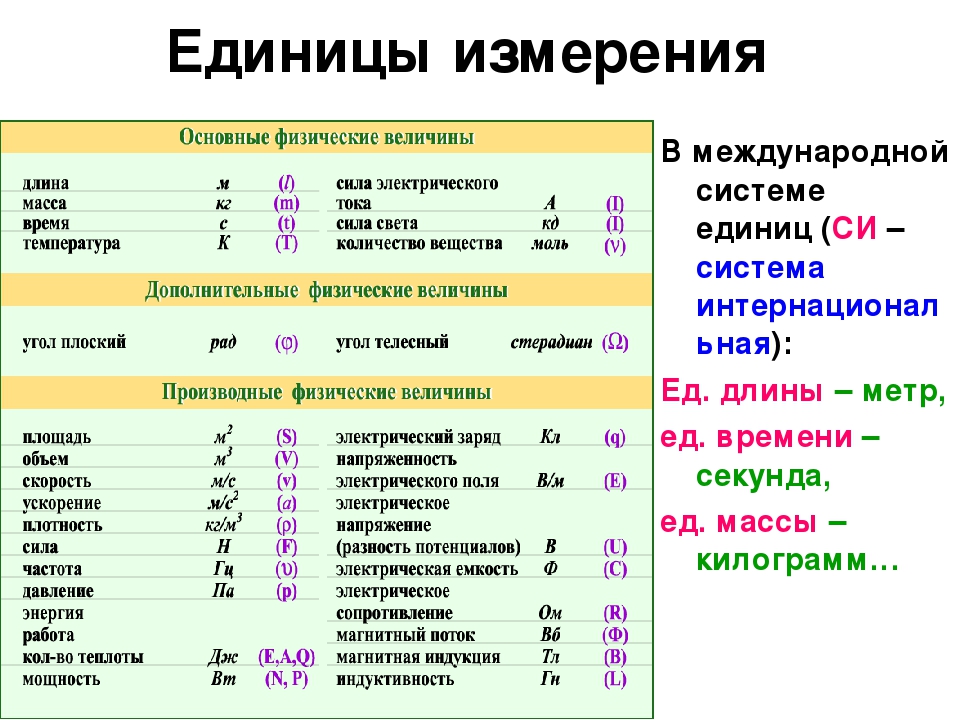 |
| Частота измерений, Гц | 20 — 100 | |
| Номинальные расстояния от оптики сенсора до поверхности, см | 5±2,10±3,15±5, 30±10, 60±20 и 130 ±40. Другие по заказу. | Указывается при заказе |
| Допустимый диапазон изменения расстояния | ±20-25% от номинала | Зависит от типа поверхности (амплитуда сигнала снижается на краях диапазона) |
| Тип излучателя | Диодный лазер видимого или ИК диапазона, 5, 12,40 мВт | класс 3B – 3R |
| Питание | 9 — 36 (импульсный преобразователь, изолированный) | Встроенные линейные стабилизаторы 5В в датчике и блоке обработки сигнала |
Потребляемая мощность, Вт Блок обработки | 0,3 — 2 Вт | |
| 1 Вт | ||
| Диапазон рабочих температур, ˚С | -20° С … + 60°С (-40…+400 в термокожухе) | -30…+50 – с системой термостабилизации (опция), (-50.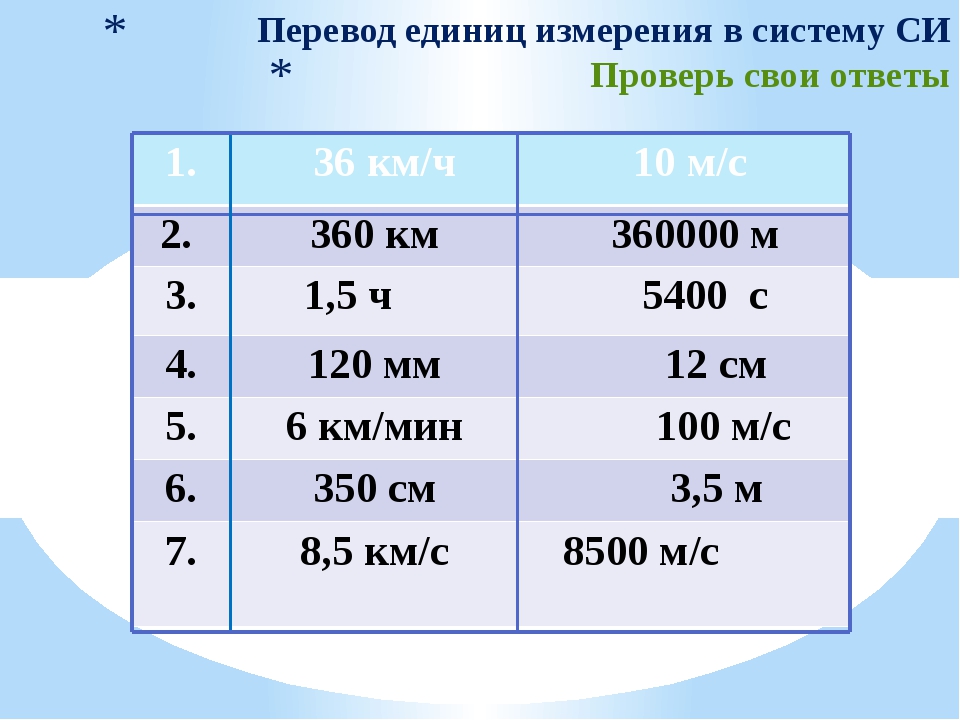 .+80˚С в защитном кожухе с подачей воздуха под давлением (опция)). .+80˚С в защитном кожухе с подачей воздуха под давлением (опция)). |
| Вес, г | 300 — 400 | |
| Размеры корпуса, мм | 120x100x35 | Без разъемов, бленд и крепежных гнезд. Подробнее — см. рисунок |
| Длина кабеля от датчика до ПРЦ обработки, м (по заказу — до 15 метров) | 2,5 | Используется стандартный кабель RS-232 или VGA с разъемами DB9. Для удлинения кабеля их можно соединять последовательно. |
| Класс защиты от внешней среды | IP67 | |
| Блок обработки сигнала: | ||
Размеры корпуса, мм Вес, г | 120х100х35 350 | |
Выходные сигналы блока обработки: Аналоговый: Частотный: Цифровой: | Скорость, 150 мВ/м/с, до 3В. Путь, 2000 Имп/м (=скорость 2000 Гц/м/с), меандр 0 – 3 В, ТТЛ совместимый, до 200 КГц. Передача всех параметров по сети LAN. | Типичные значения, могут настраиваться пользователем (см. Разрядность ЦАП и частоты – 12 бит. |
| Физическая задержка обновления выходных сигналов (latency) | 9 – 31 мс | Стабильна при данной частоте измерений(=½ времени измерения), без усреднения. Подробнее см. далее. |
| Поставляемое ПО для работы с ИСД-5 | — Программа для считывания данных по сети, отображение данных и параметров датчика, сохранение в файл ASCII. — Программа для диагностики датчика. — Пример работы в LabView 8.2.1 — DLL считывания данных по сети для встраивания в ПО пользователя. — Конфигурирование параметров – по сети, через любой браузер. | Подробнее см. далее. Возможно создание специализированного ПО по ТЗ заказчика. |
Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Чтобы сразу практиковаться, приходите в современную школу для подростков Skysmart. Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → |
Средняя путевая скорость V ср. V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это
длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже разбираемся, как строить графики кинематических величин
и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии. 2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8
м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Примеров механического движения в жизни — масса. Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!
Новое небо: как в России за одну ночь изменилась схема воздушного движения
- Павел Аксенов
- Би-би-си
Автор фото, Getty Images
В ночь на четверг в России начала действовать новая система воздушного движения. Эту реформу можно сравнить с одновременным изменением правил дорожного движения и сети автомобильных дорог. Пилоты теперь беспокоятся о безопасности полетов, а авиакомпании пытаются приспособиться к переменам. Зачем нужны были изменения и как теперь будут летать самолеты над Россией?
Новая система воздушного движения в России заработает в полночь по всемирному координированному времени — или в три часа по московскому.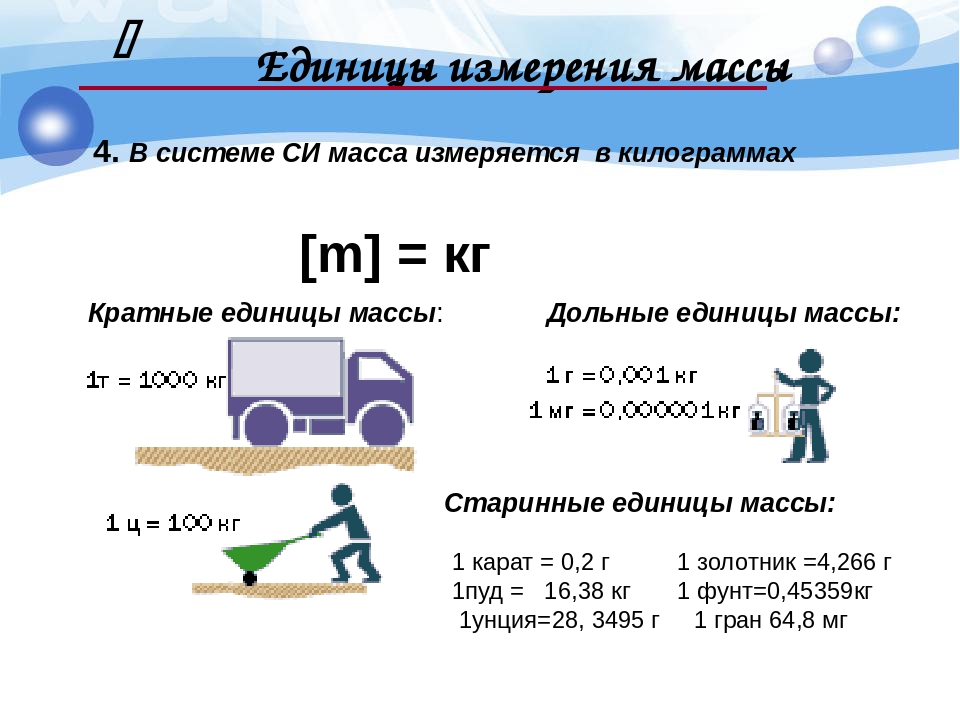
Некоторые правила вступят в силу по всей стране, некоторые изменения коснутся только московского аэроузла, но, поскольку он связан авиационными маршрутами с соседними, то они окажут влияние на всю европейскую часть российского воздушного пространства.
Изменения затронут районы полетной информации Москвы, Архангельска, Вологды, Екатеринбурга, Котласа, Ростова-на-Дону, Самары, Санкт-Петербурга, Сыктывкара и Тюмени.
Эта реформа призвана упростить работу экипажей самолетов и диспетчеров, а также уменьшить задержки во время полетов.
В декабре 2019 года Максим Акимов, который на тот момент занимал пост вице-премьера и как раз отвечал за транспорт, заявил, что новая схема позволит авиакомпаниям на 15% сократить время нахождения самолетов в московской воздушной зоне, на 14% снизится расход топлива, а время задержек при взлетах и посадках уменьшится на 70%.
С другой стороны, как выяснилось за несколько дней до вводе этой схемы, электронная навигационная система, которую используют российские летчики во время полета, не была полностью готова к нововведениям — в нее не были загружены данные многих российских аэропортов. Теперь в течение некоторого времени пилотам необходимо будет вносить эти сведения вручную, читать бумажные карты, а также активно пользоваться в полете подсказками диспетчеров.
Теперь в течение некоторого времени пилотам необходимо будет вносить эти сведения вручную, читать бумажные карты, а также активно пользоваться в полете подсказками диспетчеров.
В компаниях отнеслись к этим изменениям всерьез. Как минимум в одной крупной российской авиакомпании S7 подготовку к работе в новых условиях прошли все пилоты. СМИ сообщали о возможной отмене части рейсов «Победы» из-за новой схемы.
Русская служба Би-би-си объясняет, зачем нужна новая схема, как она будет работать и как к ней относятся пилоты.
Футы вместо метров и сложных формул
Два главных нововведения системы — измерение высоты полета в футах, а не метрах, а также измерение давления — до сих пор оно отсчитывалось от давления на уровне взлетно-посадочной полосы каждого аэродрома, а теперь будет отсчитываться от уровня моря. Это очень важные изменения.
Что происходит сейчас. Воздушное пространство делится на верхнее, где самолеты летят от одного пункта к другому, и нижнее, где они маневрируют, готовясь к посадке или после взлета.
До сих пор в России высота полета в «верхнем» пространстве измерялась в футах, как и во всем мире, а высота в «нижнем» — в метрах.
Иностранные самолеты, как и современные российские, на которых летают авиакомпании, используют систему измерения высоты в футах. До сих пор такая практика создавала неудобства для работы экипажа, которому приходилось пересчитывать высоту при переходе из одного пространства в другое по формуле, а также используя специальные таблицы перевода некоторых часто встречающихся высот из метров в футы, которые крепились в кабине (это упрощало работу в условиях повышенной занятости экипажа). Эти расчеты, например, нужны были для связи с диспетчером.
Что меняется. Теперь для оценки высоты полета самолета в кабине на приборах, при переговорах пилотов и общении экипажа с диспетчерами будут использоваться только футы, хотя диспетчеры по просьбе пилота могут выдать ему информацию в метрах.
Правда, экипажам старых советских самолетов, например Ан-2 или Ту-154, придется теперь наоборот пересчитывать свою высоту, которая на приборах будет показана в метрах, в футы.
Зачем это нужно. Это было необходимо сделать для того, чтобы привести стандарты российской гражданской авиации к мировым, освободить экипаж от ненужной заботы по пересчету данных и упростить общение с диспетчерами.
Как рассказал во время онлайн-семинара в начале ноября глава Межрегиональной общественной организации пилотов и граждан-владельцев воздушных судов Владимир Тюрин, метрическую систему будет продолжать использовать МЧС, министерство обороны, ФСБ, а также прочие государственные службы, имеющие свою авиацию — в их составе больше самолетов, построенных или разработанных в советское время и рассчитанных на метрическую систему.
Измерять высоту в метрах также придется при заходе на посадку в отдельные, например, военные аэродромы.
После перехода России на футы измерять высоту в нижнем воздушном пространстве в метрах будет только одна страна — Таджикистан, рассказал Тюрин. Высоту в метрах во всех пространствах — и в верхнем, и в нижнем — измеряют в Китае, Монголии и Северной Корее.
В советские времена высота во всех пространствах тоже измерялась в метрах. На ее измерение в футах в верхнем воздушном пространстве Россия перешла В 2011 году.
Уровень моря вместо уровня аэропорта
Что происходит сейчас. Второе важное изменение — измерение давления. Вернее, та точка, от которой его надо отсчитывать. Давление воздуха — важный параметр в авиации, поскольку оно служит для определения высоты.
До сих пор в России использовалась система калибровки альтиметров — приборов для измерения высоты таким образом, чтобы они отсчитывали высоту от уровня, на котором расположена взлетно-посадочная полоса.
Эта система в авиации называется QFE. Она не очень удобна, поскольку требует постоянного внесения корректировок в приборы, ведь самолет летит из аэропорта, расположенного на одной высоте, в аэропорт, расположенный на другой. QFE аэродрома назначения пилоту сообщает диспетчер.
Что изменится. Теперь российская гражданская авиация будет использовать другую систему, где каждый альтиметр будет откалиброван по уровню моря, а садиться самолет будет на аэродром с поправкой на его высоту.
Теперь российская гражданская авиация будет использовать другую систему, где каждый альтиметр будет откалиброван по уровню моря, а садиться самолет будет на аэродром с поправкой на его высоту.
Другими словами, пилот всегда будет знать свою высоту относительно уровня моря, но ему надо будет каждый раз делать поправку на то, что поверхность земли под ним с этим уровнем не совпадает.
Зачем это нужно. Это, во-первых, освободит экипаж от калибровки альтиметров, ведь теперь они всегда будут мерять давление относительного одного «нулевого» показателя.
Во-вторых, все самолеты в одной воздушной зоне будут отсчитывать свою высоту от некоего единого для всех уровня, что упростит управление воздушным движением.
В третьих, это также приведет систему воздушного движения в России к мировым стандартам.
Эти два новых правила будут действовать на всей территории Российской Федерации.
Новая схема полетов над Москвой
Что происходит сейчас. Нововведение, которое касается только Московского узлового диспетчерского района (МУДР), но также окажет заметное влияние и на соседние районы — в нем полностью изменена схема полетов. Таким образом изменения коснутся всей европейской части России.
Нововведение, которое касается только Московского узлового диспетчерского района (МУДР), но также окажет заметное влияние и на соседние районы — в нем полностью изменена схема полетов. Таким образом изменения коснутся всей европейской части России.
МУДР включает в себя пространство вокруг Москвы. Его границы проходят на удалении 150-180 километров. В пределах МУДР расположены аэропорты Домодедово, Шереметьево, Внуково и 13 аэродромов государственной и экспериментальной авиации.
Полет в гражданской авиации строится вокруг так называемых аэронавигационных точек. Этими точками на аэронавигационных картах покрыт весь мир. Для каждой из них определены географические координаты, а также принадлежность к определенному государству и диспетчерской зоне.
Автор фото, Marina Lystseva/TASS
Подпись к фото,
В новой системе воздушного движения взлетные курсы самолетов не будут пересекаться
Каждая точка обозначается пятибуквенным кодом. Иногда такой код выбирают созвучным с местом на карте, городом, горой или другим местом на карте, но чаще всего он не значит ничего.
Иногда такой код выбирают созвучным с местом на карте, городом, горой или другим местом на карте, но чаще всего он не значит ничего.
Пилоты строят маршрут полета от точки к точке, внося их в бортовой компьютер самолета. Этими же точками пользуются и аэронавигационные службы, выстраивающие схемы захода на посадку в аэропорт, взлета из него, стандартные маршруты полетов.
Что изменится. Нововведения, которые коснутся МУДР, полностью перестроят этот район — изменится расположение и названия точек, маршруты движения, границы различных аэронавигационных районов, даже стандартные схемы полета самолетов, например, в зоне ожидания.
Зачем это нужно. Реформа схемы воздушного движения позволит выстроить маршруты движения самолетов более оптимально, так, чтобы они не пересекались, например, на взлете и посадке.
Это поможет, в частности, в случае, когда один самолет вылетает из аэропорта, а второй собирается заходить на посадку и его курс находится в опасной близости со взлетным курсом первого.
Кроме того, воздушное движение в московском аэронавигационном районе осложнено наличием различных запретных зон, также осложняющих маневрирование самолета в воздухе.
Как рассказал на семинаре Владимир Тюрин, эти проблемы касались и обычных пассажиров, которые прилетали в Москву, например, вечером, во время активного воздушного движения — иногда самолет десятки минут кружил перед посадкой в ожидании своей очереди.
Он также рассказал, что для ожидающих самолетов будет введена так называемая «веерная» схема полета, которая позволит более оперативно перестраиваться из полетного режима ожидания и заходить на посадку, чем сейчас, когда самолеты движутся по овальной траектории.
Активность радиообмена пилотов и диспетчеров также будет заметно снижена за счет того, что воздушные потоки будут разведены — пилотам гораздо реже будет нужна помощь диспетчера.
Задача новой системы — оптимизировать воздушное движение так, чтобы самолет как можно меньше находился в воздухе в районе Москвы.
Последствия: необновленные карты и посадки по бумажным картам
Реформа организации воздушного движения в России — сложная задача. Она требует внесения изменений в огромное число документов, перенастройку аппаратуры и работы многих людей и служб.
В результате за несколько дней до начала работы выяснилось, что из-за большого объема информации компании, предоставляющие аэронавигационные услуги, в частности — готовящие электронные карты для навигационных приборов — не успели внести в них все изменения.
На мировом рынке аэронавигационных услуг существует два крупных игрока — компании Jeppesen (подразделение корпорации Boeing) и Lido (входит в Lufthansa Group). В России действуют системы обеих этих компаний — часть авиаперевозчиков использует одну, часть другую.
РБК обратило внимание на внутреннюю презентацию авиакомпании «Аэрофлот», в которой говорилось об этой проблеме. У Русской службы Би-би-си имеется аналогичный документ авиакомпании Azur Air, в котором перечислены аэропорты, о которых в системе Jeppesen отсутствует обновленная информация.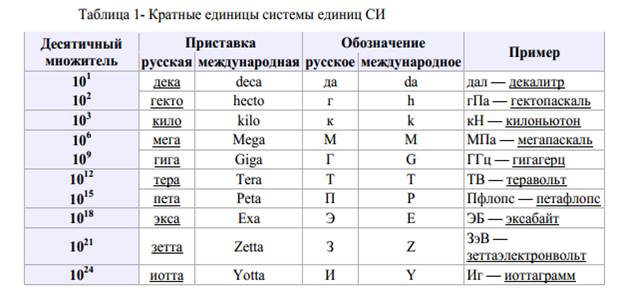
Автор фото, Getty Images
Подпись к фото,
При посадке теперь экипажи будут измерять высоту в футах
Это аэропорты Раменского, Ярославля, Магаса, Нарьян-Мара, Грозного, Таганрога, Астрахани, Белоярского, Советского, Ижевска, Кирова (Победилово), Кургана, Калуги (Грабцево), Иваново (Южный), Липецка, Ухты, Воркуты, Пензы, Курска, Петрозаводска.
Компания Jeppesen, как говорится в документе Azur Air, обещает полностью исправить ситуацию только к следующему циклу обновления в конце декабря.
Полеты в зонах, где были изменены аэронавигационные точки и маршруты, дело довольно сложное, рассказал Би-би-си пилот одной из российских авиакомпаний, он не уполномочен давать комментарии СМИ. Если раньше при подготовке к полету в навигационную систему просто вносились их названия, а она выстраивала маршрут на их основе, то теперь каждый раз перед полетом надо фактически внести в него координаты точек, которых пока нет в системе, а также высоту и скорость самолета для каждой из них.
Другой пилот — командир воздушного судна в компании «Аэрофлот» Андрей Литвинов — считает, что пилоты вполне смогут воспользоваться и бумажными картами: «Если там каких то схем нет в электронном виде — значит, будут им перед вылетом давать бумажные карты. Мы всю жизнь летали по бумажным картам и никаких проблем».
Глава Росавиации Александр Нерадько 24 ноября написал письмо в российские авиакомпании, призвав их подготовить экипажи для полетов с использованием процедуры векторения.
В таком режиме полета диспетчер дает пилоту четкое направление движения — курс, высоту, скорость. После нескольких последовательных указаний диспетчера самолет заходит на посадку, используя бортовую аппаратуру и наземные системы.
В компаниях отнеслись к этим изменениям всерьез. Как минимум в одной крупной российской авиакомпании S7 подготовку к работе в новых условиях прошли все пилоты. СМИ сообщали о возможной отмене более 100 рейсов «Победы» из-за новой схемы.
Впоследствии, как сообщает агентство РБК, авиакомпания отменила более 100 рейсов, и, кроме того, ввела в состав экипажей на некоторых других летчиков-инструкторов, которые будут помогать экипажу справляться со сложностями в полете.
Русская служба Би-би-си обратилась в несколько российских авиакомпаний, включая «Победу» с вопросом о том, как они собираются решать эту проблему.
Автор фото, Getty Images
Подпись к фото,
Высоту в верхнем воздушном пространстве измеряют в футах в России с 2011 года
Опрошенные Би-би-си пилоты считают, что главной причиной такой ситуации стала Росавиация, которая слишком поздно предоставила информацию в соответствующие структуры.
«Привело к этой ошибке то, что Росавиация не заблаговременно сообщила о переходе. Это надо было заранее делать, вносить все данные. Но вот они этого не сделали», — рассказал Би-би-си Андрей Литвинов.
Другой российский пилот, пожелавший остаться неназванным, рассказал, что российские диспетчерские службы тренируются уже несколько месяцев, готовясь к переходу на новую систему, а летный состав авиакомпаний никаких тренировок не проходил.
Единицы измерения скорости
☰
В международной системе единиц СИ скорость измеряется в метрах в секунду (м/с). Однако, нередко скорость измеряют в километрах в час (км/ч). Также иногда используют другие единицы измерения.
При решении задач важно уметь переводить скорость из одних единиц измерения в другие, так как бывает, что в задаче одни величины даны в системе СИ, а другие — нет.
Если скорость тела равна 1 км/ч, то чему она будет равна в пересчете на метр в секунду? В 1 километре 1000 метров. В 1 часе 60 минут, в каждой минуте 60 секунд, таким образом в 1 часе 60 * 60 = 3600 секунд. Значит,
1 км/ч = 1 * 1000 м / 3600 с = 0,27(7) м/c (≈ 0,28 м/с)
Если скорость тела равна 360 км/ч, то в пересчете на м/с получим:
1 км/ч = 360 * 1000 м / 3600 с = 3600 м / 36 с = 100 м/с.
Что, если нам нужно км/ч выразить в км/с. Например, скорость ракет и спутников при взлете очень большая, и выражать ее в метрах и часах не рационально.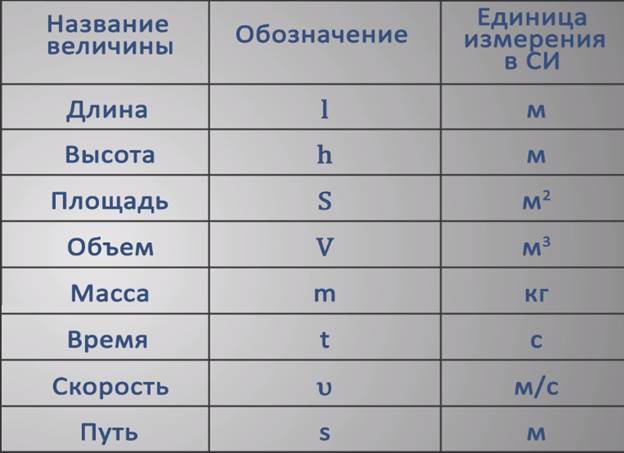 Поэтому не очень подходят единицы км/ч и м/с. Допустим, дана скорость равная 54000 км/ч, надо выразить в км/с:
Поэтому не очень подходят единицы км/ч и м/с. Допустим, дана скорость равная 54000 км/ч, надо выразить в км/с:
54000 км/ч = 54000 км / 3600 c = 15 км/с
Выше переводились более крупные единицы в более мелкие. Теперь рассмотрим примеры, когда более мелкие единицы надо перевести в более крупные.
Если скорость тела равна 1 м/с, то чему она будет равна при пересчете в км/ч? 1 метр составляет тысячную долю километра, т. е. 0,001 км = 1 м. Другими словами, надо 1 поделить на 1000 (1/1000). Секунда составляет 1/3600 долю часа. Таким образом, получаем:
1 м/с = 1 * (1/1000) км / (1/3600) ч = 3600 / 1000 (км/ч) = 3,6 км/ч
Если скорость тела равна 50 м/с, то получить ее в км/ч можно так:
(50 / 1000) км / (1/3600) ч = (5 / 100) * 3600 (км/ч) = 5 * 36 (км/ч) = 180 км/ч
или так, учитывая, что мы знаем, сколько км/ч равен 1 м/с:
50 м/c * 3,6 км/ч = 180 км/ч
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению. ..
..
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки.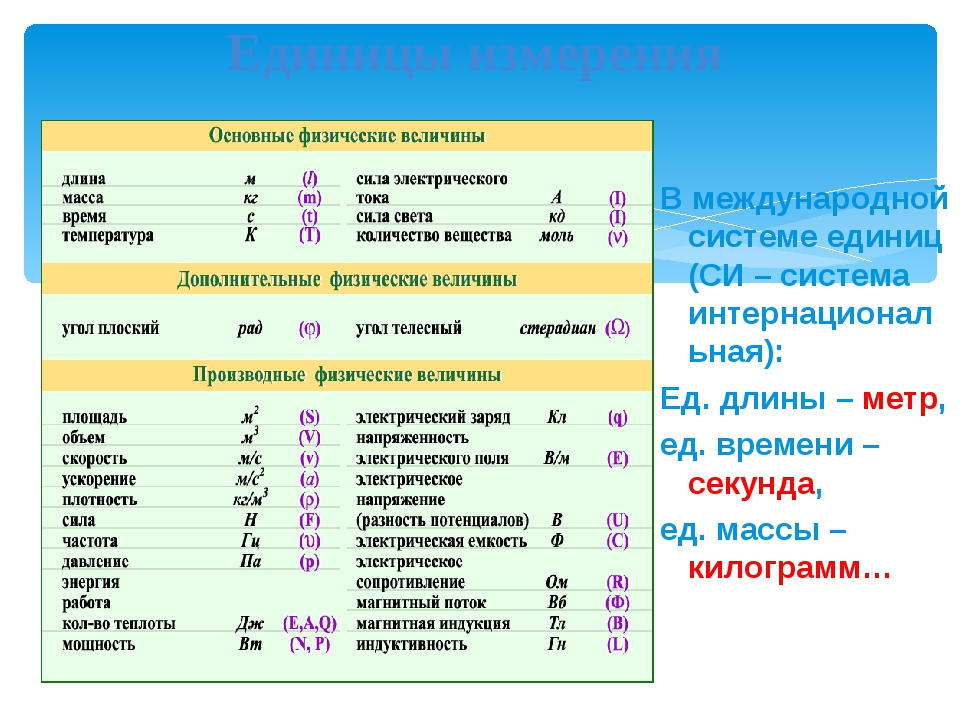 их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Расстояние и смещение — Резюме — Гипертекст по физике
- … движение
- смещение
- скорость…
Гипертекст по физике
© 1998–2021 Гленн Элерт
Автор, иллюстратор, веб-мастер
Нет постоянных условий.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снарядов
- Параметрические уравнения
- Динамика I: Сила
- Силы
- Сила и масса
- Действие-реакция
- Масса
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Кадры справки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые машины
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Вращательная динамика
- Статика вращения
- Угловой момент
- Энергия вращения
- Прокатный
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Простой генератор гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа вещества
- Газовые законы
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (световой)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводников
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- цепей постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC цепи
- Цепи РЛ
- Цепи LC
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Относительность
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированные вещества
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика вкусов
- Стандартная модель
- Помимо стандартной модели
- Относительность
- Фонды
- Квартир
- Международная система единиц
- Гауссова система единиц
- Британо-американская система единиц
- Разные единицы
- Время
- Преобразование единиц
- Измерение
- Значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение векторов
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая таблица элементов
- Люди в физике
- Квартир
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- glennelert.нас
- Behance
- Твиттер
- YouTube
- Аффилированные сайты
- hypertextbook.com
- midwoodscience.org
- Предисловие
Измерения в химии — Химия
Глава 1 — Измерения в химии
Это содержимое также можно загрузить в виде PDF-файла для печати или интерактивного PDF-файла.Для интерактивного PDF-файла требуется Adobe Reader для полной функциональности.
Этот текст опубликован под лицензией Creative Commons, для ссылки и адаптации нажмите здесь.
Разделы:
Раздел 1: Химия и вещества
Что такое химия?
Физические и химические свойства
Элементы и соединения
Смеси
Состояния материи
Раздел 2: Как ученые изучают химию
Научный метод
Раздел 3: Научная нотация
Видеоуроки
Практические задачи
Раздел 4: Единицы измерения
Международная система единиц и метрическая система
Производные единицы СИ
Раздел 5: Проведение измерений в лаборатории
Precision vs.Точность
Значимые цифры
Точные числа
Правила округления
Видеоурок
Расчеты со значащими цифрами
Преобразование и важность единиц
Коэффициенты преобразования
Краткое содержание главы
Список литературы
Раздел 1: Химия и вещества
Что такое химия?
Все вокруг нас состоит из химикатов.От цвета, который делает розу такой красной, до бензина, которым наполняются наши автомобили, и кремниевых чипов, питающих наши компьютеры и сотовые телефоны… Химия повсюду! Понимание того, как химические молекулы образуются и взаимодействуют для создания сложных структур, позволяет нам использовать силу химии и использовать ее, как набор инструментов, для создания многих современных достижений, которые мы наблюдаем сегодня. Это включает в себя достижения в медицине, связи, транспорте, строительной инфраструктуре, науке о продуктах питания и сельском хозяйстве, а также почти во всех других технических областях, которые вы можете себе представить.
Химия — одна из отраслей науки. Наука — это процесс, с помощью которого мы узнаем о естественной Вселенной, наблюдая, проверяя, а затем создавая модели, объясняющие наши наблюдения. это процесс, с помощью которого мы узнаем о естественной Вселенной, наблюдая, проверяя, а затем создавая модели, которые объясняют наши наблюдения. Поскольку физическая вселенная настолько обширна, существует множество различных областей науки (рис. 1.1). Таким образом, химия изучает материю, биология изучает живые существа, а геология изучает горные породы и землю.Математика — это язык науки, и мы будем использовать его для передачи некоторых идей химии.
Хотя мы разделяем науку на разные области, между ними есть много общего. Например, некоторые биологи и химики так много работают в обеих областях, что их работа называется биохимией. Точно так же геология и химия пересекаются в области, называемой геохимией. На рисунке 1.1 показано, сколько отдельных областей науки связаны между собой.
Рисунок 1.1: Отношения между некоторыми из основных отраслей науки. Химия находится более или менее посередине, что подчеркивает ее важность для многих областей науки.
Физические и химические свойства
Часть понимания материи заключается в том, чтобы ее описать. Один из способов, которым химики описывают материю, — это относить разные свойства к разным категориям. Свойства, которые химики используют для описания материи, делятся на две основные категории.Физические свойства — это характеристики, которые описывают вещество, такие как температура кипения, точка плавления и цвет. Физические изменения, такие как плавление твердого вещества в жидкость, не изменяют химическую структуру этого вещества. Химические свойства — это характеристики, которые описывают, как химическая структура вещества изменяется во время химической реакции. Примером химического свойства является воспламеняемость — способность материала гореть — потому что горение (также известное как горение) изменяет химический состав материала.
Элементы и соединения
Любой образец вещества, который имеет одинаковые физические и химические свойства во всем образце, называется веществом. Есть два типа веществ. Вещество, которое не может быть разбито на химически более простые компоненты, является элементом. Алюминий, который используется в банках с газировкой, является элементом. Вещество, которое можно разбить на химически более простые компоненты (поскольку оно содержит более одного элемента), представляет собой соединение. Вода — это соединение, состоящее из водорода и кислорода.Сегодня в известной вселенной около 118 элементов, которые организованы на фундаментальной диаграмме, называемой Периодической таблицей элементов (рис. 1.2). Напротив, на сегодняшний день ученые идентифицировали десятки миллионов различных соединений.
Наименьшая часть элемента, которая поддерживает идентичность этого элемента, называется атомом. Атомы очень крошечные; чтобы сделать линию длиной в 1 дюйм, вам понадобится 217 миллионов атомов железа! Точно так же самая маленькая часть соединения, которая поддерживает идентичность этого соединения, называется молекулой.Молекулы состоят из атомов, которые соединены вместе и ведут себя как единое целое (рис. 1.2). Ученые обычно работают с миллионами атомов и молекул одновременно. Когда ученый работает
Рисунок 1.2: ( Верхняя панель) Периодическая таблица элементов — это организованная диаграмма, которая содержит все известные химические элементы. ( Нижняя панель ) Слева от стрелки показан один атом кислорода и два атома водорода. Каждый из них представляет собой отдельные элементы.Когда они объединены с правой стороны, они образуют единую молекулу воды (H 2 O). Обратите внимание, что вода определяется как соединение, потому что каждая отдельная молекула состоит из более чем одного типа элементов, в данном случае из одного атома кислорода и двух атомов водорода.
с большим количеством атомов или молекул одновременно, ученый изучает макроскопическое представление Вселенной. Однако ученые могут также описывать химические явления на уровне отдельных атомов или молекул, что называется микроскопической точкой зрения.В этой книге мы увидим примеры как макроскопических, так и микроскопических точек зрения (рис. 1.3).
Рисунок 1.3: Сколько молекул необходимо для точки в предложении? Хотя мы не замечаем этого с макроскопической точки зрения, материя состоит из микроскопических частиц, настолько крошечных, что нужны миллиарды их, чтобы образовать пятнышко, которое мы можем увидеть невооруженным глазом. X25 и X400000000 указывают, сколько раз изображение было увеличено.
Смеси
Материал, состоящий из двух или более веществ, представляет собой смесь.В смеси отдельные вещества сохраняют свою химическую идентичность. Многие смеси представляют собой очевидные комбинации двух или более веществ, например смесь песка и воды. Такие смеси называют гетерогенными смесями. В некоторых смесях компоненты настолько тесно связаны, что действуют как единое вещество, хотя это не так. Смеси с однородным составом называются гомогенными смесями. Гомогенные смеси, которые перемешиваются настолько тщательно, что ни один компонент не может наблюдаться независимо от другого, называются растворами.Растворенный в воде сахар является примером решения. Металлический сплав, такой как сталь, является примером твердого раствора. Воздух, состоящий в основном из азота и кислорода, представляет собой газообразный раствор.
Рисунок 1.4: Гетерогенные и однородные смеси. Смесь содержит более одного вещества. На верхней панели вы видите пример неоднородной смеси масла и воды. Смесь неоднородна, потому что вы можете визуально увидеть два разных компонента в смеси.На нижней панели вы видите пример однородной смеси, кофе. Он однороден, потому что вы не можете различить множество различных компонентов, из которых состоит чашка кофе (вода; кофеин; кофейные алкалоиды и дубильные вещества). Все выглядит одинаково. Если смесь однородная, а также прозрачная или прозрачная, ее называют раствором. В нашем примере кофе — это раствор; однако концентрированный эспрессо может быть очень непрозрачным и представлять собой только гомогенную смесь, а не раствор.
Состояния материи
Другой способ классификации материи — описать ее как твердое тело, жидкость или газ, как это было сделано в примерах растворов выше. Эти три описания, каждое из которых подразумевает, что материя обладает определенными физическими свойствами, представляют три фазы материи. Твердое тело имеет определенную форму и определенный объем. Жидкости имеют определенный объем, но не определенную форму; они принимают форму своих контейнеров. У газов нет ни формы, ни объема, они расширяются, заполняя свои сосуды.Каждый день мы сталкиваемся с материей в каждой фазе. Фактически, мы регулярно встречаем воду во всех трех фазах: лед (твердая), вода (жидкость) и пар (газ).
Из нашего опыта работы с водой мы знаем, что вещества могут переходить из одной фазы в другую при подходящих условиях. Обычно изменение температуры вещества (и реже оказываемого на него давления) может вызвать фазовый переход или физический процесс, в котором вещество переходит из одной фазы в другую (рис. 1.5). Фазовые изменения имеют определенные названия в зависимости от того, какие фазы задействованы, как показано в Таблице 1.1.
Рисунок 1.5. Анализ фазовых изменений. ( Верхняя панель ) Фотография кипящей воды демонстрирует фазовый переход воды из жидкой фазы в газообразную. Обратите внимание, что фазовые изменения — это физическое свойство молекулы. Вода остается неизменной по химическому составу (H 2 O) в твердом, жидком или газообразном состоянии. ( Нижняя панель ) Изменение температуры может вызвать фазовые изменения. Выше — температурная шкала фазовых переходов воды.Если добавить тепла к твердому льду, вода растает при 0 o C и закипит при 100 o C. Если вы уберете тепло от газообразной воды, она будет конденсироваться в жидкое состояние при 100 o C и замерзнуть 0 o C.
Итак, рис. 1.6 «Классификация материи» иллюстрирует взаимосвязь между различными способами классификации материи.
Рисунок 1.6 Классификация материи. Вещество можно классифицировать по-разному в зависимости от его свойств
(Вернуться к началу)
Раздел 2: Как ученые изучают химию
Научный метод
Как работают ученые? Как правило, они следуют процессу, называемому научным методом.Научный метод — это организованная процедура изучения ответов на вопросы. Чтобы найти ответ на вопрос (например, «Почему птицы летают к экватору Земли в холодные месяцы?»), Ученый выполняет следующие шаги, которые также показаны на рисунке 1.7.
Рис. 1.7 Общие шаги научного метода. В реальной жизни шаги могут быть не такими четкими, как описано здесь, но большинство научных работ следует этому общему плану.
Предложите гипотезу. Ученый генерирует проверяемую идею или гипотезу, чтобы попытаться ответить на вопрос или объяснить, как устроена естественная вселенная. Некоторые люди используют слово теория вместо гипотезы, но слово гипотеза — правильное слово в науке. В научных приложениях слово теория — это общее утверждение, описывающее большой набор наблюдений и данных. Теория представляет собой высший уровень научного понимания и построена на широком спектре фактических знаний или данных.
Проверить гипотезу. Ученый оценивает гипотезу, разрабатывая и проводя эксперименты для ее проверки. Если гипотеза проходит проверку, это может быть правильным ответом на вопрос. Если гипотеза не проходит проверку, это может быть плохой ответ.
При необходимости уточните гипотезу. В зависимости от результатов экспериментов, ученый может захотеть изменить гипотезу, а затем снова проверить ее. Иногда результаты показывают, что исходная гипотеза полностью ошибочна, и в этом случае ученый должен будет разработать новую гипотезу.
Не все научные исследования достаточно просты, чтобы их можно было разделить на эти три отдельных этапа. Но эти шаги представляют собой общий метод, с помощью которого ученые узнают о нашей естественной вселенной.
(Вернуться к началу)
Раздел 3: Научная нотация
Изучение химии может включать очень большие числа. Он также может включать в себя очень маленькие числа. Записать такие числа и использовать их в длинной форме проблематично, потому что мы потратим слишком много времени на написание нулей и, вероятно, сделаем много ошибок! Решение этой проблемы есть.Это называется научным обозначением.
Научная нотация позволяет нам выражать очень большие и очень маленькие числа, используя степень 10.
Напомним, что:
10
0 = 1 10 1 = 10 10 2 = 100
10
3 = 1000 10 4 = 10000 10 5 = 100000
Как видите, степень возведения 10 равна количеству нулей, следующих за 1. Это поможет определить, какой показатель использовать, когда мы выражаем числа в экспоненциальной нотации.
Возьмем очень большое число:
579, 000, 000, 000
и выразите это в экспоненциальной нотации.
Сначала мы находим коэффициент, который представляет собой число от 1 до 10, которое будет умножено на 10 в некоторой степени.
Наш коэффициент: 5,79
Это число будет умножено на 10 в некоторой степени. Теперь давайте разберемся, что это за сила.
Мы можем сделать это, посчитав количество позиций, которые стоят между концом исходного числа и новой позицией десятичной точки в нашем коэффициенте.
5. 7 9 0 0 0 0 0 0 0 0 0
↑ ↑
Сколько там позиций?
Мы видим, что между десятичной запятой и концом исходного числа есть 11 позиций. Это означает, что наш коэффициент 5,79 будет умножен на 10 в 11-й степени.
Наше число, выраженное в экспоненциальном представлении:
5,79 x 10
11
А как насчет очень маленьких чисел?
Вы можете вспомнить, что:
10
-1 = 0.1 10 -2 = 0,01 10 -3 = 0,001
10
-4 = 0,0001 10 -5 = 0,00001
Количество пробелов справа от десятичной точки для нашей 1 равно числу в экспоненте, стоящему за отрицательным знаком. Это полезно иметь в виду, когда мы выражаем очень маленькие числа в научных обозначениях.
Вот очень маленькое число:
0,0000642
Выразим это число в научных обозначениях.
Наш коэффициент будет 6.42
Это число будет умножено на 10 в некоторой степени, которая будет отрицательной. Давайте выясним правильную мощность. Мы можем выяснить это, посчитав, сколько позиций находится между десятичной точкой в нашем коэффициенте и десятичной точкой в нашем исходном числе.
0. 0 0 0 0 6 4 2
↑ ↑
Сколько позиций?
Между нашей новой десятичной точкой и десятичной точкой в исходном числе 5 позиций, поэтому наш коэффициент будет умножен на 10 в отрицательной пятой степени.
Наш номер в экспоненциальном формате:
6,42 х 10
-5
Вы можете использовать эти методы для выражения любого большого или малого числа в экспоненциальной нотации.
ВИДЕОУЧЕБНИК ДЛЯ ЗНАЧИТЕЛЬНЫХ ЦИФР:
(Вернуться к началу)
Раздел 4: Единицы измерения
Международная система единиц и метрическая система
Международная система единиц, сокращенно SI от французской Système International D’unités, является основной системой единиц измерения, используемой в науке.С 1960-х годов Международная система единиц была принята на международном уровне как стандартная метрическая система. Базовые единицы СИ основаны на физических стандартах. Определения базовых единиц СИ изменялись и продолжают изменяться, а новые базовые единицы добавляются по мере развития науки. Каждая базовая единица СИ, кроме килограмма, описывается стабильными свойствами Вселенной.
Существует семь базовых единиц, которые перечислены в Таблице 1.2. В химии в основном используются пять основных единиц измерения: моль для количества, килограмм для массы, метр для длины, второй для времени и кельвин для температуры.Градус Цельсия ( o C) также обычно используется для измерения температуры. Числовое соотношение между градусами Кельвина и градусами Цельсия выглядит следующим образом:
К =
o С + 273
Размер каждой базовой единицы определяется международным соглашением. Например, килограмм определяется как масса специального металлического цилиндра, хранящегося в хранилище во Франции (рис. 1.8). Другие базовые единицы имеют аналогичные определения. Размеры базовых блоков не всегда удобны для всех измерений.Например, метр — довольно большая единица измерения ширины чего-то столь узкого, как человеческий волос. Вместо того, чтобы сообщать диаметр волоса как 0,00012 м или даже 1,2 × 10 -4 м, SI также предоставляет серию префиксов, которые могут быть прикреплены к единицам измерения, создавая единицы, которые больше или меньше по степени 10, известные как метрическая система.
Рисунок 1.8 Килограмм. Эталон килограмма — платино-иридиевый цилиндр, хранящийся в особом хранилище во Франции.Источник: Wikimedea (https://commons.wikimedia.org/wiki/File:National_prototype_kilogram_K20_replica.jpg)
Общие префиксы и их мультипликативные коэффициенты перечислены в Таблице 1.3 «Префиксы, используемые с единицами SI». (Возможно, вы уже заметили, что основная единица измерения килограмм представляет собой комбинацию префикса килограмм, означающего 1000 ×, и единицы массы, грамма.) Некоторые префиксы образуют кратную исходной единице: 1 килограмм равен 1000 граммов ( или 1 кг = 1 000 г), а 1 мегаметр равен 1 000 000 метров (или 1 Мм = 1 000 000 м).Другие префиксы составляют часть исходной единицы. Таким образом, 1 сантиметр равен 1/100 метра, 1 миллиметр равен 1/1000 метра, 1 микрограмм равен 1/1000000 грамма и так далее.
Масса
Килограмм является основной единицей массы в Международной системе единиц. Килограмм равен 1000 граммам. Грамм — это относительно небольшое количество массы, поэтому большие массы часто выражаются в килограммах. Когда измеряются очень крошечные количества вещества, мы часто используем миллиграммы, которые равны 0.001 грамм. Есть множество больших, меньших и промежуточных единиц массы, которые также могут быть подходящими. В конце 18 века килограмм был массой литра воды. В 1889 году из платино-иридиевого сплава был изготовлен новый международный прототип килограмма. Килограмм равен массе этого международного прототипа, который хранится в Париже, Франция.
Масса и вес — это не одно и то же. Хотя мы часто используем термины масса и вес как синонимы, у каждого из них есть свое определение и использование.Масса объекта — это мера количества вещества в нем. Масса (количество вещества) объекта остается неизменной независимо от того, где он находится. Например, перемещение кирпича на Луну не приводит к исчезновению или удалению какой-либо находящейся в нем материи.
Вес объекта определяется силой, которую гравитация оказывает на объект. Вес равен массе объекта, умноженной на местное ускорение свободного падения. Таким образом, на Земле вес определяется силой притяжения между объектом и Землей.Поскольку сила тяжести неодинакова в каждой точке поверхности Земли, вес объекта не постоянен. Гравитационное притяжение объекта меняется в зависимости от его положения относительно Земли или другого объекта, создающего гравитацию. Например, человек, который весит 180 фунтов на Земле, весил бы всего 45 фунтов, если бы он находился в неподвижном положении на высоте 4000 миль над поверхностью Земли. Этот же человек весил бы на Луне всего 30 фунтов, потому что гравитация Луны составляет лишь одну шестую гравитации Земли.Однако масса этого человека будет одинаковой в каждой ситуации. Для научных экспериментов важно измерять массу вещества, а не вес, чтобы сохранить согласованность результатов независимо от того, где вы проводите эксперимент.
Длина
Единица измерения длины в системе СИ — метр. В 1889 году измеритель представлял собой слиток из платино-иридиевого сплава, хранившийся в условиях, установленных Международным бюро стандартов.В 1960 году это определение стандартного измерителя было заменено определением, основанным на длине волны излучения криптона-86. В 1983 году это определение было заменено следующим: метр — это длина пути, пройденного светом в вакууме за интервал времени в секунду.
Температура
В научном контексте слова тепло и температура НЕ означают одно и то же. Температура представляет собой среднюю кинетическую энергию частиц, составляющих материал.Повышение температуры материала увеличивает его тепловую энергию. Тепловая энергия — это сумма кинетической и потенциальной энергии частиц, из которых состоит материал. Предметы не «содержат» тепло; скорее они содержат тепловую энергию. Тепло — это движение тепловой энергии от более теплого объекта к более холодному. Когда тепловая энергия переходит от одного объекта к другому, температура обоих объектов изменяется.
Термометр — это прибор, измеряющий температуру. Название состоит из слова «термо», что означает тепло, и «метр», что означает измерение.Температура вещества прямо пропорциональна средней кинетической энергии, которую оно содержит. Чтобы средняя кинетическая энергия и температура вещества были прямо пропорциональны, необходимо, чтобы при нулевой температуре средняя кинетическая энергия также была равна нулю. Это было необходимо для использования в расчетах в науке для третьей шкалы температур, в которой ноль градусов соответствует нулевой кинетической энергии, то есть точке, в которой молекулы перестают двигаться. Эта температурная шкала была разработана лордом Кельвином.Лорд Кельвин заявил, что не существует верхнего предела того, насколько горячими могут быть вещи, но есть предел того, насколько холодными могут быть вещи. В 1848 году Уильям лорд Кельвин разработал идею абсолютного нуля, то есть температуры, при которой молекулы перестают двигаться и, следовательно, имеют нулевую кинетическую энергию. Это известно как температурная шкала Кельвина.
Шкала Цельсия основана на температуре замерзания и кипения воды. Таким образом, 0 o C — это точка замерзания воды, а 100 o C — температура кипения воды.Большинство из нас знакомы с температурами ниже точки замерзания воды. Должно быть очевидно, что даже несмотря на то, что температура воздуха может составлять -5 o C, молекулы воздуха все еще движутся (т.е. 0 o C не является абсолютным нулем). Такие вещества, как газообразный кислород и газообразный азот, уже расплавились и превратились в пар при температурах ниже -150 o C.
Шкала Фаренгейта также определяется точкой замерзания и температурой кипения воды. Однако шкала отличается от шкалы Кельвина и Цельсия.По шкале Фаренгейта точка замерзания воды составляет 32 o F, а точка кипения воды составляет 212 o F. Для преобразования шкалы Фаренгейта в шкалу Цельсия можно использовать следующие преобразования:
[
o C] = ([ o F] -32) × 5/9 или [ o F] = [ o C] × 9/5 + 32
Температурная шкала Кельвина имеет нулевое значение при абсолютном нуле (определено как -273,15 o C) и использует ту же шкалу градусов, что и шкала Цельсия.Следовательно, математическая связь между шкалой Цельсия и шкалой Кельвина составляет
.
К =
o С + 273,15
В случае шкалы Кельвина знак градуса не используется. Температуры выражаются просто как 450 К и всегда положительны.
Время
Единицей измерения времени в системе СИ является секунда. Второй изначально определялся как крошечная часть времени, необходимого Земле для обращения вокруг Солнца. С тех пор его определение несколько раз менялось.Определение секунды (установлено в 1967 г. и подтверждено в 1997 г.): продолжительность 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Сумма
Химики используют термин моль для обозначения большого количества атомов или молекул. Подобно тому, как дюжина подразумевает 12 вещей, моль (моль) представляет 6,022 × 10 23 единиц. Число 6,022 × 10 23 , названное числом Авогадро в честь химика XIX века Амедео Авогадро, — это число, которое мы используем в химии для обозначения макроскопических количеств атомов и молекул.Таким образом, если у нас есть 6,022 × 10 23 атомов кислорода, мы говорим, что у нас есть 1 моль атомов кислорода. Если у нас есть 2 моля атомов Na, у нас будет 2 × (6,022 × 10 23 ) атомов Na, или 1,2044 × 10 24 атомов Na. Аналогично, если у нас есть 0,5 моль молекул бензола (C 6 H 6 ), мы имеем 0,5 × (6,022 × 10 23 ) C 6 H 6 молекул, или 3,011 × 10 23 C 6 H 6 молекул.
Производные единицы СИ
Производные единицы представляют собой комбинации основных единиц СИ.Единицы можно умножать и делить, так же как числа можно умножать и делить. Например, площадь квадрата со стороной 2 см составляет 2 см × 2 см или 4 см2 (читается как «четыре сантиметра в квадрате» или «четыре квадратных сантиметра»). Обратите внимание, что мы возведем в квадрат единицу длины, сантиметр, чтобы получить производную единицу площади, квадратный сантиметр.
Объем
Объем — важная величина, в которой используется производная единица. Объем — это количество пространства, которое занимает данное вещество, геометрически определяемое как длина × ширина × высота.Каждое расстояние может быть выражено с помощью единицы измерения, поэтому объем имеет производную единицу m × m × m, или m 3 (читается как «кубические метры» или «кубические метры»). Кубический метр — это довольно большой объем, поэтому ученые обычно выражают объемы в единицах 1/1000 кубического метра. У этой единицы есть собственное название — литр (L). Литр немного больше 1 кварты США по объему. (Таблица 1.4) дает приблизительные эквиваленты для некоторых единиц, используемых в химии.) Как показано на Рисунке 1.9 «Литр», литр также равен 1 000 см 3 .По определению, в 1 л содержится 1000 мл, поэтому 1 миллилитр и 1 кубический сантиметр представляют один и тот же объем.
1 мл = 1 см 3
Рисунок 1.9: Литр. Литр — это куб со стороной 10 см (1/10 метра). Миллилитр, 1/1000 литра, равен 1 кубическому сантиметру (1 см 3 ).
Энергетика
Энергия, еще одна важная величина в химии, — это способность выполнять работу.Например, перемещение коробки с книгами из одной стороны комнаты в другую требует энергии. Его производная единица: кг · м 2 / с 2 . (Точка между килограммами и м 2 единиц означает, что единицы умножаются вместе, а затем весь член делится на s 2 .) Поскольку эта комбинация громоздка, эта совокупность единиц переопределяется как джоуль (Дж) , которая является единицей измерения энергии в системе СИ. Также широко используется более старая единица энергии — калория (cal). Всего:
4.184 Дж = 1 ккал
Обратите внимание, что это отличается от нашего обычного использования больших «калорий» или «кал», указанных на пищевых упаковках в США. Большой «Cal» на самом деле является килокалорией или ккал (рис. 1.10). Обратите внимание, что все химические процессы или реакции происходят с одновременным изменением энергии, и эта энергия может храниться в химических связях.
Рисунок 1.10: Разница между килокалориями в научном и обычном использовании . Калории, представленные на упаковке пищевых продуктов, на самом деле относятся к килокалориям с научной точки зрения.
Плотность
Плотность определяется как масса объекта, деленная на его объем; он описывает количество вещества, содержащегося в данном объеме пространства.
плотность = масса / объем
Таким образом, единицы плотности — это единицы массы, разделенные на единицы объема: г / см3 или г / мл (для твердых и жидких веществ соответственно), г / л (для газов), кг / м3 и т. Д. . Например, плотность воды составляет около 1,00 г / мл, а плотность ртути — 13.6 г / мл. Ртуть более чем в 13 раз плотнее воды, а это означает, что она содержит в 13 раз больше вещества в том же объеме пространства. Плотность воздуха при комнатной температуре около 1,3 г / л.
Раздел 5: Проведение измерений в лаборатории
Прецизионность против точности
Важно отметить различную терминологию, которую мы используем, когда говорим в науке. Один из таких наборов терминов — точность и аккуратность. Хотя в ненаучном сообществе понятие «точность» и «аккуратность» часто используются как синонимы, очень важно понимать разницу между этими терминами.Точность говорит вам, насколько близки два измерения друг к другу, а точность говорит вам, насколько близко измерение к известному значению. Измерение может быть точным, но не точным, или точным, но неточным; эти два термина НЕ связаны. Хорошую аналогию можно найти в игре в дартс (рис. 1.11). Игрок, который всегда попадает в одно и то же место слева от доски для дротика, будет точным, но не очень точным. Однако игрок в дартс, который находится по всей доске, но в среднем попадает в центр доски, будет точным, но не точным.Хороший игрок в дартс, как и хороший ученый, хочет быть точным и аккуратным.
Рисунок 1.11: Разница между точностью и прецизионностью. С помощью игры в дартс можно показать разницу между точностью и точностью.
Взято из: https://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Reliability_and_validity.svg/717px-Reliability_and_validity.svg.png
Обычно в лаборатории точность — это мера того, насколько хорошо откалибровано ваше оборудование.Например, если ваши весы откалиброваны правильно, вы можете проводить очень точные, повторяющиеся измерения, но измерения не будут отражать истинное значение. С другой стороны, точность обычно определяется тем, насколько осторожен ученый при проведении измерений. Если вы проявите неосторожность и пролили часть образца по пути, ваши измерения в повторных экспериментах не будут точными, даже если ваши весы будут точными.
Значимые цифры
Важно понимать, что значения в научных измерениях никогда не бывают точными на 100%.Наши инструменты измеряют только с определенной степенью точности. Таким образом, мы можем выбрать разные инструменты для измерения в зависимости от уровня точности, который нам необходим для эксперимента. Из-за присущей неточности любого измеряемого числа мы должны отслеживать различные уровни точности каждого числа со значащими цифрами. Под значащими цифрами измеряемой величины понимаются все достоверно известные цифры и первая неопределенная или оценочная цифра. Нет смысла сообщать какие-либо цифры после первой неопределенной, поэтому это последняя цифра, указанная в измерении.Нули используются, когда необходимо поставить значащие цифры на их правильные позиции. Таким образом, нули могут быть значащими цифрами, а могут и не быть. Значимые цифры применимы в реальном мире, поскольку они позволяют нам количественно оценить точность любого типа измерения. Чтобы определить, сколько чисел в измерении имеет значение, вы можете следовать осторожному набору правил, показанных ниже и справа.
Рисунок 1.12: Измерение объекта по правильному количеству значащих цифр.
Сколько цифр должно быть показано в этом измерении?
Правильный ответ — 3! Два, которые вы знаете наверняка + предполагаемое положение… для этого значения оно будет близко к 1.37
Точные числа
Точные числа — это числа, которые не измеряются научными приборами. Они либо используются в качестве определений для определения понятия или терминологии, либо создаются путем подсчета общего количества чего-то присутствующего. Примером точного числа может быть количество яиц в коробке или определенная единица измерения, например 100 см на 1 м. Точные числа, такие как количество людей в комнате, НЕ влияют на количество значащих цифр в расчетах, сделанных с измеренными значениями.
Правила округления
В научных операциях правила округления могут немного отличаться от тех, к которым вы привыкли. Обычные правила округления предполагают, что если число 4 или меньше, оно должно быть округлено до меньшего числа, тогда как если оно равно 5 или больше, оно должно быть округлено в большую сторону. Однако обратите внимание, что 5 находится прямо посередине и вызывает проблемы при использовании этих обычных правил округления. Если у вас есть большой набор данных чисел, который вам нужно округлить, использование этого правила округления приведет к смещению в вашем наборе данных (т.е. 4/9 времени вы будете округлять в меньшую сторону, и 5/9 времени вы будете округлять в большую сторону). В большом наборе данных такое смещение недопустимо.
В научном округлении мы обычно используем правило под названием «Округление до четного». В этой системе округления правила одинаковы для 4 и ниже, вы округляете до меньшего числа, а для 6 и выше вы округляете до большее число. Однако, если число, которое вы округляете, равно 5, вы округляете до четного числа. Это помогает уменьшить смещение выборки, которое может возникнуть при округлении больших наборов данных.
Расчеты со знаками
Прежде чем выполнять какие-либо научные вычисления, необходимо осознать, что все измеряемые числа хороши ровно настолько, насколько хорош инструмент, используемый для их измерения. Даже с использованием самого лучшего доступного инструмента измеренное число никогда не будет точным на 100%. Ученые используют правило «достаточно хорошей» точности, означающее, что мы допускаем некоторую погрешность, присущую каждому измерению, которое мы делаем, при условии, что конечный результат достаточно близок к желаемому.Эта концепция становится опасной, когда мы начинаем использовать эти «достаточно хорошие» числа для любых расчетов, если мы не будем внимательно следить за нашими значащими цифрами, наши числа могут быстро потерять свой «достаточно хороший» статус. Чтобы защитить свои «достаточно хорошие» числа, научное сообщество установило определенные правила для выполнения любых расчетов; в этом разделе нам нужно уделить внимание только двум очень важным правилам: правилу сложения / вычитания и правилу умножения / деления.
Правило сложения / вычитания:
- Найдите число с наименьшим количеством десятичных знаков и отслеживайте количество десятичных знаков
- Выполните сложение / вычитание
- Округлите окончательный ответ до наименьшего числа десятичных знаков, найденных на этапе 1
Правило умножения / деления:
- Подсчитайте количество значащих цифр в каждом числе (отслеживайте количество значащих цифр)
- Выполните умножение / деление
- Округлите окончательный ответ до наименьшего числа значащих цифр, найденных на этапе 1
Расчет сложных задач:
- Используя порядок операций, разбейте проблему на несколько этапов
- Выполните любые шаги сложения / вычитания в соответствии с правилом сложения / вычитания (пока не округляйте, просто отслеживайте правильное количество десятичных знаков при нахождении числа значащих цифр)
- Выполните умножение / деление по правилу умножения / деления
- Округлите окончательный ответ до правильного числа значащих цифр
Преобразование и важность единиц
Умение преобразовывать одну единицу в другую — важный навык.Например, медсестра с таблетками аспирина 50 мг, которая должна дать пациенту 0,2 г аспирина, должна знать, что 0,2 г равняется 200 мг, поэтому необходимо 4 таблетки. К счастью, есть простой способ преобразовать одну единицу в другую.
Коэффициенты преобразования
Если вы выучили единицы СИ и префиксы, описанные в разделе 1.4 «Единицы измерения», то вы знаете, что 1 см составляет 1/100 метра или:
100 см = 1 м
Предположим, мы делим обе части уравнения на 1 м (как число, так и единицу; обратите внимание, что критически важно всегда записывать ваши единицы! Это позволяет избежать путаницы и ошибок при преобразовании.):
Пока мы выполняем одну и ту же операцию с обеими сторонами знака равенства, выражение остается равенством. Посмотрите на правую часть уравнения; теперь у него такое же количество в числителе (вверху), что и в знаменателе (внизу). Любая дробь, имеющая одинаковое количество в числителе и знаменателе, имеет значение 1:
.
Мы знаем, что 100 см — это 1 м, поэтому у нас одинаковое количество сверху и снизу нашей дроби, хотя оно выражается в разных единицах.Дробь, у которой в числителе и знаменателе есть эквивалентные величины, но выраженные в разных единицах, называется коэффициентом преобразования
.
Обратите внимание, что коэффициенты преобразования могут быть записаны с использованием любого члена в числителе или знаменателе и использоваться в зависимости от проблемы, которую вы хотите решить. Это потому, что оба члена равны 1
Вот простой пример. Сколько сантиметров в 3.55 м? Возможно, вы сможете определить ответ в уме. Если в каждом метре 100 см, то 3,55 м равняется 355 см. Чтобы решить проблему более формально с коэффициентом преобразования, мы сначала записываем заданное нам количество, 3,55 м. Затем мы умножаем это количество на коэффициент преобразования, который совпадает с умножением на 1. Мы можем записать 1 как 100 см / 1 м и умножить:
Поскольку m, сокращение для метров, встречается как в числителе, так и в знаменателе нашего выражения, они сокращаются.Последний шаг — выполнить расчет, который остается после отмены единиц. Обратите внимание, что КРИТИЧНО сохранить правильные единицы в окончательном ответе, иначе это не будет иметь смысла. Обобщенное описание этого процесса выглядит следующим образом:
количество (старые единицы) × коэффициент пересчета = количество (новые единицы)
Вам может быть интересно, почему мы используем кажущуюся сложной процедуру прямого преобразования. В более поздних исследованиях проблемы преобразования, с которыми вы столкнетесь, не всегда будут такими простыми.Если вы овладеете техникой применения коэффициентов пересчета, вы сможете решить большое количество разнообразных задач.
В предыдущем примере мы использовали дробь 100 см / 1 м в качестве коэффициента преобразования. Равен ли коэффициент преобразования 1 м / 100 см также 1? Да, это так; в числителе у него такое же количество, что и в знаменателе (за исключением того, что они переворачиваются). Почему мы не использовали этот коэффициент преобразования? Если бы мы использовали второй коэффициент преобразования, исходная единица не была бы отменена, и результат был бы бессмысленным.Вот что мы получили бы:
НЕПРАВИЛЬНОЕ ИСПОЛЬЗОВАНИЕ ФАКТОРА ПРЕОБРАЗОВАНИЯ !!
Вы можете видеть, что ни одна из единиц не отменена. Чтобы ответ был осмысленным, мы должны сконструировать коэффициент преобразования в форме, которая приведет к отмене исходной единицы. На рис. 1.13 «Концептуальная карта конверсий» показана концептуальная карта для построения правильного преобразования.
Рис. 1.13. Концептуальная карта конверсий. Вот как вы создаете коэффициент преобразования для преобразования одной единицы в другую.
(Вернуться к началу)
Краткое содержание главы
Ссылки:
Материалы Главы 1 были адаптированы и изменены из следующих ресурсов Creative Commons, если не указано иное:
1. Анонимно. (2012) Введение в химию: общие, органические и биологические (V1.0). Опубликовано по лицензии Creative Commons by-NC-sa 3.0. Доступно по адресу: http://2012books.lardbucket.org/books/introduction-to-chemistry-general-organic-and-biological/index.html
2. Поульсен Т. (2010) Введение в химию. Опубликовано по лицензии Creative Commons by-NC-sa 3.0. Доступно по адресу: http://openedgroup.org/books/Chemistry.pdf
3. OpenStax (2015) Атомы, изотопы, ионы и молекулы: строительные блоки. OpenStax CNX. Доступно по адресу: http://cnx.org/contents/be8818d0-2dba-4bf3-859a-737c25fb2c99@12.
Международная система измерений (SI)
Метрическая система была разработана во время Французской революции, а стандарты для метра и килограмма были установлены 22 июня 1799 года.
Метрическая система представляла собой элегантную десятичную систему, в которой единицы одного и того же типа определялись степенью десяти. Степень разделения была относительно простой, поскольку различные единицы были названы с предисловиями, указывающими порядок величины разделения. Таким образом, 1 килограмм был 1000 граммов, потому что килограммов — означает 1000.
В отличие от английской системы, в которой 1 миля составляет 5280 футов, а 1 галлон равен 16 чашкам (или 1229 драмов, или 102,48 джиггера), метрическая система явно привлекала ученых.В 1832 году физик Карл Фридрих Гаусс активно продвинул метрическую систему и использовал ее в своей основательной работе по электромагнетизму.
Формализация измерения
Британская ассоциация развития науки (BAAS) начала свою деятельность в 1860-х годах, систематизируя необходимость согласованной системы измерения в научном сообществе. В 1874 году BAAS представила систему измерений cgs (сантиметр-грамм-секунда). В системе cgs в качестве основных единиц использовались сантиметр, грамм и секунда, а другие значения были взяты из этих трех основных единиц.Измерение cgs для магнитного поля было гаусс , из-за более ранней работы Гаусса по этому вопросу.
В 1875 году было введено соглашение о едином метре. В то время существовала общая тенденция к тому, чтобы блоки были практичными для использования в соответствующих научных дисциплинах. Система cgs имела некоторые недостатки масштаба, особенно в области электромагнетизма, поэтому в 1880-х годах были введены новые единицы измерения, такие как ампер (для электрического тока), ом (для электрического сопротивления) и вольт (для электродвижущей силы).
В 1889 году в соответствии с Общей конвенцией мер и весов (или CGPM, аббревиатура французского названия) система перешла на новые базовые единицы измерения: метр, килограмм и секунда. Начиная с 1901 года было предложено ввести новые базовые блоки, например, для электрического заряда, чтобы завершить систему. В 1954 году в качестве основных единиц были добавлены ампер, Кельвин (для температуры) и кандела (для силы света).
CGPM переименовал ее в Международную систему измерений (или SI, от французского Systeme International ) в 1960 году.С тех пор моль был добавлен в качестве базового количества вещества в 1974 году, таким образом доведя общее количество базовых единиц до семи и завершив современную систему единиц СИ.
Базовые блоки SI
Система единиц СИ состоит из семи основных единиц, а также ряда других единиц, производных от этих основ. Ниже приведены базовые единицы СИ вместе с точными определениями , которые показывают, почему определение некоторых из них заняло так много времени.
- метр (м) — Базовая единица длины; определяется длиной пути, пройденного светом в вакууме за промежуток времени 1/299 792 458 секунды.
- килограмм (кг) — Базовая единица массы; равняется массе международного прототипа килограмма (введен в эксплуатацию ГКПМ в 1889 г.).
- секунда (с) — Базовая единица времени; длительность 9 192 631 770 периодов излучения, соответствующая переходу между двумя сверхтонкими уровнями основного состояния в атомах цезия 133.
- ампер (А) — Базовая единица электрического тока; постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины, с ничтожно малым поперечным сечением цепи и размещать на расстоянии 1 метра в вакууме, создавал бы между этими проводниками силу, равную 2 x 10 -7 ньютона на метр длины.
- Кельвин (градусы К) — основная единица термодинамической температуры; доля 1 / 273,16 термодинамической температуры тройной точки воды (тройная точка — это точка на фазовой диаграмме, где три фазы сосуществуют в равновесии).
- моль (моль) — Базовая единица вещества; количество вещества в системе, которая содержит столько элементарных объектов, сколько атомов в 0,012 кг углерода 12. При использовании моля должны быть указаны элементарные объекты, которые могут быть атомами, молекулами, ионами, электронами, другими частицами, или определенные группы таких частиц.
- кандела (кд) — Базовая единица силы света; сила света в заданном направлении источника, который испускает монохроматическое излучение с частотой 540 x 10 12 герц и имеет силу излучения в этом направлении 1/683 ватт на стерадиан.
Производные единицы SI
Из этих базовых единиц выводятся многие другие единицы. Например, единица измерения скорости в системе СИ — м / с (метр в секунду), используя базовую единицу длины и базовую единицу времени для определения длины, пройденной за заданный период времени.
Перечисление всех производных единиц здесь было бы нереалистичным, но в целом, когда термин определен, соответствующие единицы СИ будут введены вместе с ними. Если вы ищете единицу, которая не определена, посетите страницу единиц СИ Национального института стандартов и технологий.
Под редакцией Энн Мари Хелменстайн, Ph.D.
7 основных единиц метрической системы
Метрическая система представляет собой структуру единиц измерения, которая выросла с момента ее рождения в 1874 году в дипломатическом соглашении до более современной Генеральной конференции по мерам и весам, или CGPM ( Conferérence Générale des Poids et Measures ).Современная система правильно называется Международной системой единиц или СИ, аббревиатура от французского Le Système International d’Unités. Сегодня большинство людей используют метрики и СИ как синонимы.
7 основных метрических единиц
Метрическая система — это основная система единиц измерения, используемая в науке. Каждая единица считается размерно независимой от других. Эти измерения представляют собой измерения длины, массы, времени, электрического тока, температуры, количества вещества и силы света.Вот определения семи основных единиц:
- Длина: метр (м) Метр — это метрическая единица измерения длины. Он определяется как длина пути, который свет проходит в вакууме за 1/299 792 458 секунды.
- Масса: Килограмм (кг) Килограмм — это метрическая единица массы. Это масса международного прототипа килограмма: стандартная платина / иридий массой 1 кг, размещенная недалеко от Парижа в Международном бюро мер и весов (BIPM).
- Время: Секунды Базовая единица времени — секунда. Второй определяется как продолжительность 9 192 631 770 колебаний излучения, соответствующих переходу между двумя сверхтонкими уровнями цезия-133.
- Электрический ток: Ампер (А) Основной единицей электрического тока является ампер. Ампер определяется как постоянный ток, который, если его поддерживать в двух бесконечно длинных прямых параллельных проводниках с ничтожно малым круглым поперечным сечением и размещать на расстоянии 1 м в вакууме, создавал бы силу между проводниками, равную 2 x 10 -7. ньютона на метр длины.
- Температура: Кельвин (K) Кельвин — это единица термодинамической температуры. Это доля 1 / 273,16 термодинамической температуры тройной точки воды. Шкала Кельвина является абсолютной шкалой, поэтому здесь нет градуса.
- Количество вещества: моль (моль) Моль определяется как количество вещества, которое содержит столько элементов, сколько атомов в 0,012 кг углерода-12. Когда используется моль, необходимо указать объекты.Например, объектами могут быть атомы, молекулы, ионы, электроны, коровы, дома или что-то еще.
- Сила света: кандела (кд) Единицей силы света или света является кандела. Кандела — это сила света в заданном направлении источника, излучающего монохроматическое излучение с частотой 540 x 10 12 герц с интенсивностью излучения в этом направлении 1/683 ватт на стерадиан.
Эти определения на самом деле являются методами реализации единицы.Каждая реализация была создана с уникальной прочной теоретической базой для получения воспроизводимых и точных результатов.
Другие важные метрические единицы
В дополнение к семи основным единицам обычно используются другие метрические единицы:
- Литр (л) В то время как метрической единицей объема является кубический метр, м 3 , наиболее часто используемой единицей измерения является литр. Литр равен по объему одному кубическому дециметру, дм 3 , что представляет собой куб, равный 0.По 1 м с каждой стороны.
- Ангстрем (Å) Один Ангстрем равен 10 -8 см или 10 -10 м. Названный в честь Андерса Йонаса Ангстрома, прибор используется для измерения длины химической связи и длины волны электромагнитного излучения.
- Кубический сантиметр (см 3 ) Кубический сантиметр — это обычная единица измерения твердого объема. Соответствующей единицей измерения объема жидкости является миллилитр (мл), который равен одному кубическому сантиметру.
метров (м) — НПЛ
С 1983 года измеритель во всем мире определяется как длина пути, проходимого светом в вакууме за промежуток времени 1/299 792 458 секунды.Это определение может быть реализовано просто и точно с использованием современных методов, а скорость света считается универсальной константой, что делает ее идеальной в качестве основы для стандарта длины.
Определение счетчика можно практически реализовать двумя способами:
Время пролета — импульс света посылается по измеряемой длине. Время, за которое свет проходит это расстояние, в секундах, умноженное на скорость света (299 792 458 метров в секунду), дает длину в метрах.Поскольку скорость света очень велика, этот метод легче применять на больших расстояниях. Однако при измерении астрономических расстояний необходимо учитывать эффекты гравитационного поля.
Интерферометрия — метод интерферометрии позволяет измерять длину в единицах длины волны света. Используя источник света известной и стабильной длины волны, можно напрямую измерить длину до 100 метров с точностью до 1 части на несколько миллионов.
Точное измерение длины и точное определение необходимы во всем современном мире.От мельчайших деталей на микрочипе, стандартной резьбы на гайках и болтах до больших сложных узлов современных авиалайнеров — взаимозаменяемость и воспроизводимость важны в глобальной экономике, где элементы поступают из разных стран, но при этом должны идеально подходить друг к другу. , первый раз.
Лазеры, используемые в настоящее время для реализации измерителя, обеспечивают очень стабильные оптические частоты (или длины волн в вакууме) за счет сервоуправления испускаемым ими светом для определенных эталонных значений поглощения в таких газах, как йод, содержащихся в небольших газовых ячейках.Однако их точность ограничена движением молекул газа в лазерном луче при комнатной температуре. Заменяя молекулы йода на атомы или ионы, такие как иттербий или стронций, которые удерживаются в электромагнитных или оптических ловушках, можно «охлаждать лазером» атомы близко к абсолютному нулю (тем самым уменьшая их движение). При таком расположении оптические опорные частоты могут быть на несколько порядков более точными, но другие ограничения, такие как атмосферные условия или стабильность материала, обычно не позволяют использовать их при прямом измерении длины на этих улучшенных уровнях.
Узнайте об исследованиях NPL в этой области
Дополнительная информация об определениях единиц СИ из BIPM
единиц, не относящихся к системе СИ — Science Learning Hub
Обычно используется ряд единиц, не относящихся к системе СИ, хотя система единиц СИ позволяет полностью охватить все научные измерения. Причины этого исторические и политические, а также повседневное удобство.
Почти все страны мира, за исключением США, Либерии и Мьянмы, приняли систему единиц СИ для повседневного коммерческого и научного использования.В 1988 году Американский Конгресс принял СИ в качестве предпочтительной системы США, но не принял эффективных законов, обеспечивающих ее соблюдение. В результате единицы измерения, обычно используемые в США, взяты из имперской системы мер и весов. Например, расстояние измеряется в дюймах, футах, ярдах и милях, а не в миллиметрах, метрах и километрах.
Некоторые британские единицы измерения (Великобритания)
Длина | Масса и вес | Объем жидкости | |||
|---|---|---|---|---|---|
12 дюймов = 1 фут | 437.5 гран = 1 унция | 20 жидких унций = 1 пинта | |||
3 фута = 1 ярд | 16 унций = 1 фунт | 4 жабры = 1 пинта | 14 фунтов = 1 стоун | 2 пинты = 1 кварта | |
8 фарлонгов = 1 миля | 8 стоунов = 1 центнер (цвт) | ||||
5280 футов = 1 миля | 20 центнеров = 1 тонна | 8 пинт = 1 галлон | |||
Некоторые часто используемые единицы, не относящиеся к СИ
Физическая величина | Единица, не относящаяся к СИ | Symbol | Коэффициент преобразования |
|---|---|---|---|
Энергия | калорий | кал | 1 кал = 4.184 Дж |
Длина | Ангстрем | 1 Å = 10 -10 м | |
тонн Масса 71 | 1 t = 10 3 кг | ||
Давление | атм | атм | 1 атм = 1.013 x 10 5 Па |
Температура | градус Цельсия | ° C | 1 ° C = 1 K |
мин | 1 мин = 60 с | ||
час | час или час | 1 час = 3600 с | |
1 d = 86400 с | |||
Объем | литр | L | 1 L = 1 дм 3 = 10 -3 |
Энергия
С тех пор, как Термин «калорийность» во многом стал частью области питания / диеты.Люди, соблюдающие диету, часто измеряют или оценивают потребление пищи и выработку энергии в калориях, а не в единицах СИ — джоулях.
Калория — это количество энергии, необходимое для повышения температуры 1 г воды на 1 ° C. Это соответствие 1: 1: 1, возможно, легче понять, чем определение джоуля: 4,18 джоуля — это количество энергии, необходимое для повышения температуры 1 г воды на 1 ° C.
На этикетках пищевых продуктов в Новой Зеландии требуется указывать информацию о содержании энергии в килоджоулях или килоджоулях и калориях.
Время
В исходной метрической системе, разработанной во Франции в 1790-х годах, была сделана попытка десятичного измерения времени. Например, день нужно было разделить на 10 часов по 100 минут в час и 100 секунд в минуту. Эта идея не прижилась, поскольку требовала переделки всех устройств для измерения времени, таких как часы. В результате, использование часов, минут и секунд с их неудобными числовыми соотношениями по-прежнему актуально.
Вторая стала универсальной базовой единицей времени:
- 1 час = 3600 с
- 1 день = 86 400 с
- 1 год ~ 31.6 мега секунд (Ms)
Давление
Единицей давления в системе СИ является паскаль (Па), где 1 Па = 1 Нм -2 .
По-прежнему широко используется термин «атмосфера», который относится к давлению, оказываемому весом атмосферы на поверхность Земли. В среднем в день на уровне моря это давление составляет 1 атмосферу, что равно 101,325 кПа.
При накачивании пневматических шин, например, на автомобилях и велосипедах, часто используется единица, не входящая в систему СИ, фунты на квадратный дюйм (psi):
Объем
Хотя литр обычно используется в качестве меры объема, он не является единицей СИ. базовая единица объема — кубический метр (м 3 ).В оригинальной французской метрической системе базовой единицей объема был литр (л), определяемый как объем 1 килограмма воды при 4 ° C. Этот объем эквивалентен 1000 см 3 и также известен как 1 дециметр в кубе (дм 3
- 1 м 3 = 1000 дм 3 = 1000000 см 3
- 1 м 3 = 1000 л = 1 000 000 мл
Литр (л) и миллилитр (мл) не являются единицами системы СИ, но, поскольку их легче писать и произносить, они широко используются.
Путаница с единицами измерения
В повседневной деятельности мы часто видим единицы измерения, которые либо неправильно написаны, либо применены:
- Торговые площадки автомобилей часто рекламируют как транспортное средство с «низким Ks», но если они имеют в виду малый километраж, то блок «км». Единица измерения «Ks» — секунда в градусах Кельвина, которая не имеет физического значения.
- Когда люди говорят о своем «счете за электроэнергию», на самом деле они имеют в виду счет за «электроэнергию». Мощность измеряется в ваттах, а энергия — в джоулях.Мы покупаем «электрическую энергию», а не электрическую «мощность» у «электростанции».
- Некоторые люди ходят в тренажерный зал, чтобы «сжечь калории», чтобы снизить свой «вес». С научной точки зрения, они расходуют энергию, измеряемую в килоджоулей, в попытке сбросить некоторую массу тела, измеряемую в килограммах.
Чаще всего такое неправильное использование не причиняет вреда. Однако использование неправильных единиц имело плачевный и дорогостоящий эффект для Mars Climate Orbiter — космического корабля, предназначенного для выхода на орбиту вокруг планеты Марс и сбора данных об атмосфере и климате Марса.
23 сентября 1999 г. Mars Climate Orbiter был потерян, когда космический аппарат вышел на более низкую траекторию орбиты, чем планировалось. Эта более низкая орбита заставила космический корабль нагреться и разрушиться, прежде чем упасть на поверхность планеты.
Основная причина этого происшествия была обнаружена в калибровочной таблице подруливающих устройств, в которой использовались британские имперские единицы вместо единиц СИ. Программное обеспечение для навигации в Лаборатории реактивного движения предполагало, что данные об импульсе двигателя будут выражаться в ньютон-секундах, но компания Lockheed Martin Astronautics, которая построила орбитальный аппарат, предоставила значения в фунт-силе секунды.Это привело к интерпретации импульса как четверть его фактического значения. В результате орбитальный аппарат упал на более низкую орбиту, для которой он не был конструктивно рассчитан.
Стоимость этой аварии оценивалась в 125 миллионов долларов.
Природа науки
Одним из ключевых аспектов природы науки является то, что она производит, требует и полагается на тщательные измерения. Тщательно разработанная Международная система единиц обеспечивает надежный способ достижения этого.Если ученые и инженеры общаются друг с другом, используя разные системы измерения, могут возникнуть дорогостоящие недопонимания.
Единицы СИ и физические стандарты
Единицы СИ, чаще называемые метрической системой, являются основой для современных калибровок.
При измерении длины мы ссылаемся на метр. История счетчика восходит к 18 веку во Франции. Да, существует реальный физический стандарт измерителя.Как и любой физический эталон, он подвержен влиянию окружающей среды. Фактически, первоначальный расчет счетчика был неправильным из-за просчета, и со временем необходимость в более стабильном определении стала очевидной. Это привело к следующему определению счетчика:
Метр — это длина пути, пройденного светом в вакууме за промежуток времени 1/299 792 458 секунды.
Есть 7 основных единиц СИ:
Было выбрано
единиц СИ, поскольку они считаются независимыми от размерности.Килограмм — это последний эталон, который еще можно привязать к реальному объекту.
Почему это важно и как это влияет на измерения и калибровку?
Ключевым моментом при любом измерении является неопределенность измерения. Это +/- в любом измерении. Подумайте об использовании линейки с делением 1/32 дюйма. Хотя вы можете догадаться, где между делениями может находиться измерение, на самом деле вы знаете только 1/32 дюйма. Если бы вы могли измерить до 1 миллионной дюйма, у вас была бы меньшая погрешность измерения, чем 1/32 дюйма.
Стремление к меньшей неопределенности измерения привело ученых к исследованиям с использованием единиц СИ для измерения. По мере развития науки вполне вероятно, что погрешность измерения будет уменьшаться.
Взгляните на картинку ниже из Великобритании.
NIST в США предлагает аналогичную картину.
Успехи в области измерений ежегодно отмечаются во Всемирный день метрологии.
Калибровочные лаборатории, аккредитованные по ISO 17025, должны продемонстрировать свою компетентность, установив непрерывную цепочку прослеживаемости до единицы СИ.
ISO / IEC 17025: 2005 Пункт 5.6.2
Прослеживаемость измерений
- 5.6.2.1 «Для калибровочных лабораторий программа калибровки оборудования должна быть спроектирована и работать так, чтобы гарантировать, что калибровки и измерения, производимые лабораторией, прослеживаются в Международной системе единиц (SI ) ( Système international d’unités ) ».
Калибровочная лаборатория устанавливает прослеживаемость своих собственных эталонов и измерительных приборов к СИ посредством непрерывной цепи калибровок или сравнений, связывающих их с соответствующими первичными эталонами единиц измерения СИ.Связь с единицами СИ может быть достигнута путем ссылки на национальные стандарты измерения. Национальные эталоны могут быть первичными эталонами, которые являются первичной реализацией единиц СИ или согласованными представлениями единиц СИ на основе фундаментальных физических констант, или они могут быть вторичными эталонами, которые являются эталонами, откалиброванными другим национальным метрологическим институтом. При использовании услуг внешней калибровки прослеживаемость измерений должна быть обеспечена за счет использования услуг калибровки из лабораторий, которые могут продемонстрировать компетентность, измерительные возможности и прослеживаемость.Сертификаты калибровки, выданные этими лабораториями, должны содержать результаты измерений, включая неопределенность измерений и / или заявление о соответствии установленным метрологическим требованиям (см. Также 5.10.4.2).
ПРИМЕЧАНИЕ 1 Калибровочные лаборатории, выполняющие требования настоящего справочника, считаются компетентными. Свидетельство о калибровке с логотипом органа по аккредитации от калибровочной лаборатории, аккредитованной для данного справочника, для соответствующей калибровки, является достаточным доказательством прослеживаемости представленных данных калибровки.
ПРИМЕЧАНИЕ 2 Прослеживаемость до единиц измерения СИ может быть достигнута путем ссылки на соответствующий первичный стандарт (см. VIM: 1993, 6.4) или путем ссылки на естественную константу, значение которой в терминах соответствующей единицы СИ известно и рекомендуется. Генеральной конференцией мер и весов (CGPM) и Международным комитетом мер и весов (CIPM).
ПРИМЕЧАНИЕ 3 Калибровочные лаборатории, которые поддерживают свой собственный первичный эталон или представление единиц СИ на основе фундаментальных физических констант, могут заявить о прослеживаемости к системе СИ только после того, как эти эталоны будут прямо или косвенно сравнены с другими аналогичными эталонами национального метрологического института.
ПРИМЕЧАНИЕ 4 Термин «идентифицированные метрологические характеристики» означает, что из сертификата калибровки должно быть ясно, с какой спецификацией сравнивались измерения, путем включения спецификации или предоставления однозначной ссылки на спецификацию.
ПРИМЕЧАНИЕ 5. Когда термины «международный стандарт» или «национальный стандарт» используются в связи с прослеживаемостью, предполагается, что эти стандарты соответствуют свойствам первичных стандартов для реализации единиц СИ.
ПРИМЕЧАНИЕ 6. Прослеживаемость до национальных эталонов не обязательно требует использования национального метрологического института страны, в которой расположена лаборатория.

 01
01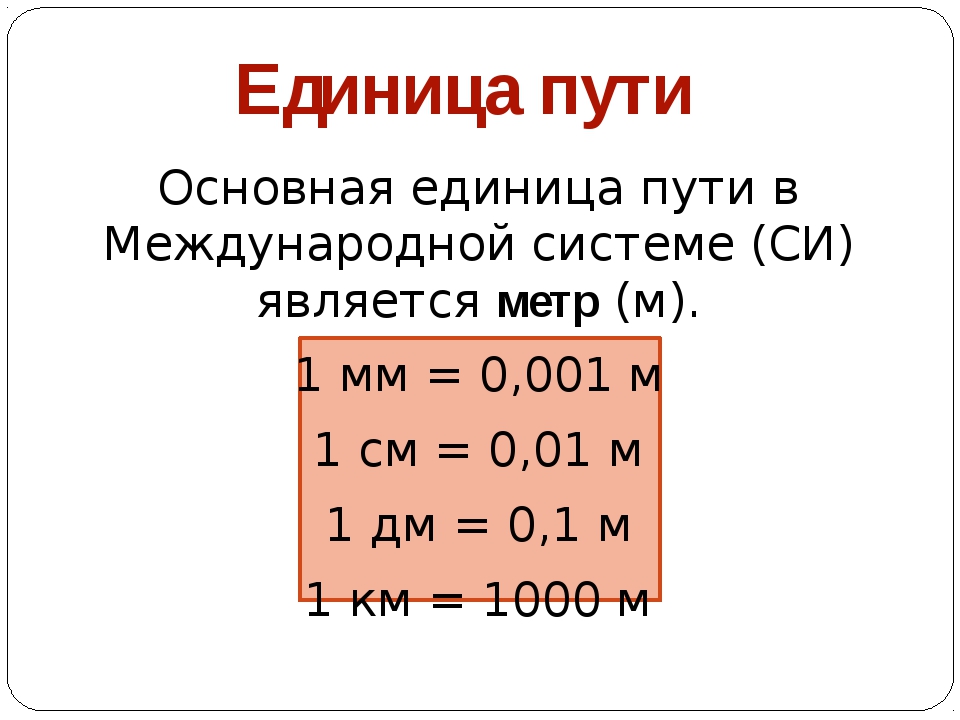 344
344 9144
9144 3048006096
3048006096 0292100584
0292100584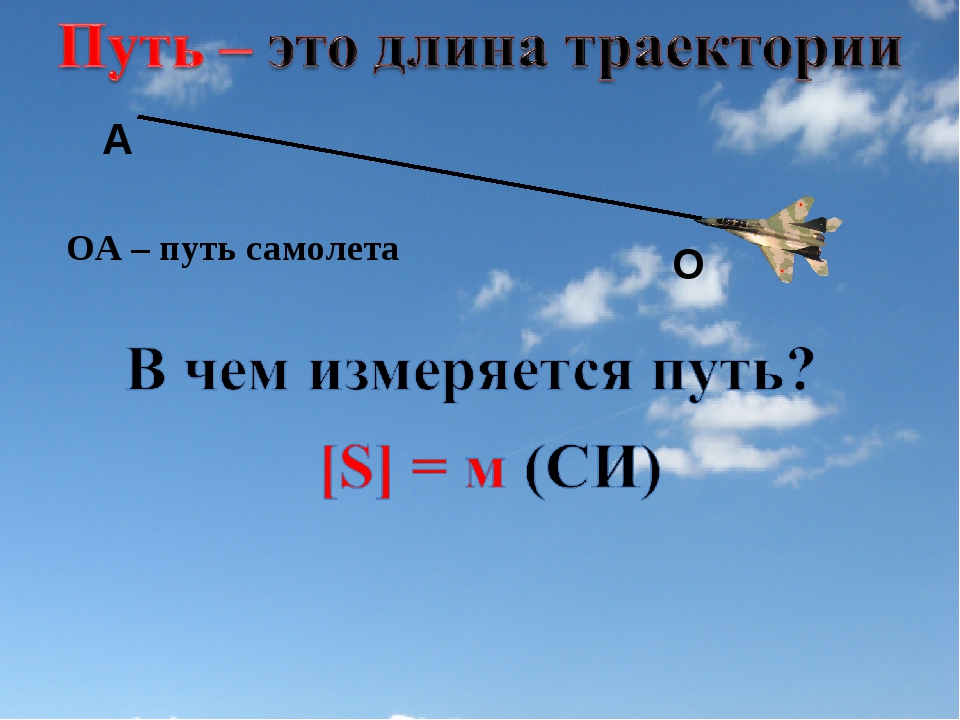
 50W
50W
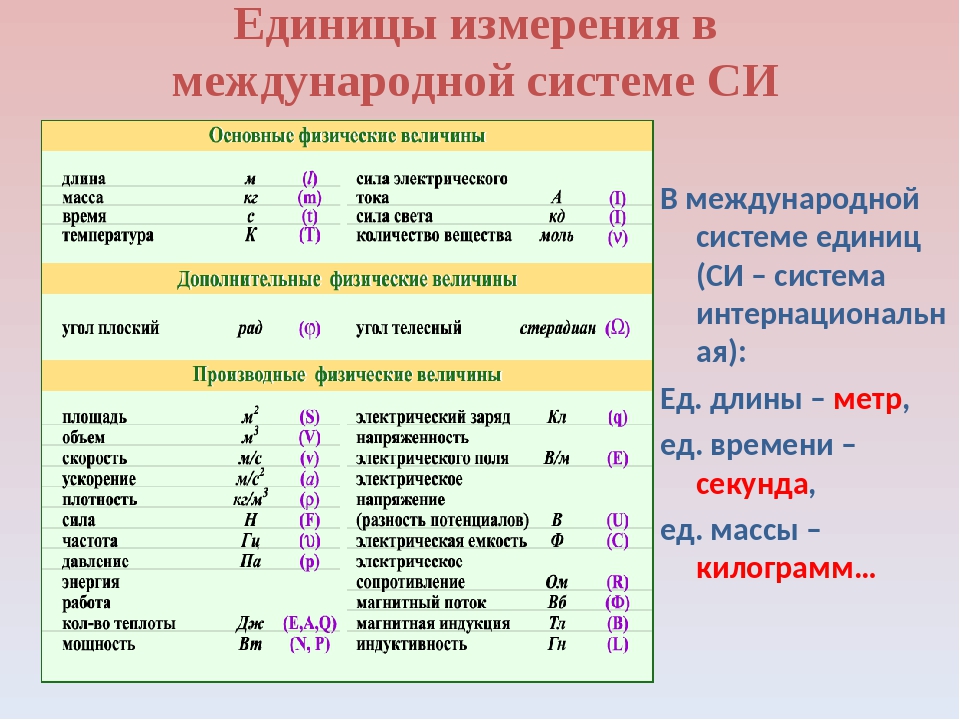 далее описание ПО).
далее описание ПО).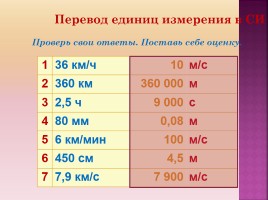 путевая = S/t
путевая = S/t