Плотность воды от давления и температуры: Плотность воды, теплопроводность и физические свойства: таблицы свойств воды
Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Свойства рабочих сред / / Вода, лед и снег / / Свойства воды под давлением (сжатой воды). 0-374 °C, 0-1000 бар. Удельный объем, плотность, энтальпия, энтропия. Таблица.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Плотность воды — определение, плотность воды и температура
Плотность воды (далее возможно ПВ) — весьма важное для всех нас свойство воды, впрочем как и все остальные 🙂
Плотность — это …
Вначале сформулируем, что такое плотность вещества как таковая, в общем.
Плотность показывает количество, какого либо вещества, выраженное в массе, на единицу объема.
ПЛОТНОСТЬ (ρ)= МАССА (M)/ОБЪЕМ (V)
Значение плотности воды
ПВ не является константой, ее величина зависит, при условии постоянного давления, от двух факторов – температуры и ее «солености». Так, например, плотность чистой пресной воды при температуре 20 °C и давлении 1 атм равняется 998,23 кг/м3, а плотность морской воды на поверхности океана ориентировочно 1027 кг/м3.
Плотность воды в зависимости от температуры
Ниже приведем изменение плотности чистой воды в зависимости от температуры:
- При – 30 °C — 0,9839 гр/см3;
- При – 20 °C — 0,9935 гр/см3;
- При – 10 °C — 0,9982 гр/см3;
- При 0 °C — 0,99987 гр/см3;
- При 1 °C — 0,99993 гр/см3;
- При 2 °C — 0,99997 гр/см3;
- При 3 °C — 0,99999 гр/см3;
- При 4 °C — 1.00000 гр/см3;
- При 5 °C — 0,99999 гр/см3;
- При 6 °C — 0,99997 гр/см3;
- При 7 °C — 0,99993 гр/см3;
- При 8 °C — 0,99988 гр/см3;
- При 9 °C — 0,99981 гр/см3;
- При 10 °C — 0,99973 гр/см3;
- При 15 °C — 0,99913 гр/см3;
- При 20 °C — 0,99823 гр/см3;
- При 25 °C — 0,99707 гр/см3;
- При 30 °C — 0,99562 гр/см3;
- При 40 °C — 0,99224 гр/см3;
- При 50 °C — 0,98807 гр/см3;
- При 60 °C — 0,98324 гр/см3;
- При 70 °C — 0,97781 гр/см3;
- При 80 °C — 0,97183 гр/см3;
- При 90 °C — 0,96534 гр/см3;
- При 100 °C — 0,95838 гр/см3.
Плотность воды — аномалия
Как мы видим, ПВ в жидком состоянии, вначале, при повышении температуры до 4-х градусов по Цельсию, увеличивается, а далее от 4 °C и выше понижается. Т. е. при 4 °C ПВ достигает своего максимального значения.
С аномалией плотности воды связаны такие факты и явления:
- При замораживании вода расширяет;
- Плотность воды в твердом состоянии — льда ниже, чем ПВ в жидком состоянии;
- У воды низкий коэффициент расширения и сжатия;
- …
Прекрасной иллюстрацией аномалии ПВ является, например, лед. Он не тонет, поскольку его плотность меньше ПВ.
Свойство воды, благодаря которому ее максимальная плотность достигается при +4 °C, имеет огромное значение для всей нашей планеты. Например, благодаря именно этому свойству пруды и другие водоемы замерзают сверху вниз, что позволяет всем формам жизни находящимся в них выжить в период сильных морозов.
Заключение
Уникальные свойства ПВ еще раз подтверждают то, что в природе все находится в гармоничной взаимосвязи, нарушать которую никак нельзя.
Плотность воды — краткое определение, значение плотности воды в зависимости от температуры и её аномалия
Статья опубликована: 2015-11-26 Автор: Waterman
Физические свойства воды :: HighExpert.RU
Вода (обычная) — вещество, описываемое химической формулой H2O, самое распространенное соединение на земле, состоящее из двух атомов водорода и одного атома кислорода, растворитель минеральных солей.
Плотность воды при различной температуре
| Температура воды | Плотность воды |
| оС | кг/м3 |
| 0 | 999,9 |
| 5 | 1000 |
| 10 | 999,7 |
| 20 | 998,2 |
| 30 | 995,7 |
| 40 | 992,2 |
| 50 | 988,1 |
| 60 | 983,2 |
| 70 | 977,8 |
| 80 | 971,8 |
| 90 | 965,3 |
| 100 | 958,4 |
Динамическая и кинематическая вязкость воды при различной температуре
| Температура | Динамическая вязкость, μ | Кинематическая вязкость, ν |
| оС | (Н • c/м 2) • 103 — [сПуаз] | м2/с • 106 — [сСтокс] |
| 0 | 1,787 | 1,787 |
| 5 | 1,519 | 1,519 |
| 10 | 1,307 | 1,307 |
| 20 | 1,002 | 1,004 |
| 30 | 0,798 | 0,801 |
| 40 | 0,653 | 0,658 |
| 50 | 0,547 | 0,658 |
| 60 | 0,467 | 0,475 |
| 70 | 0,404 | 0,413 |
| 80 | 0,355 | 0,365 |
| 90 | 0,315 | 0,326 |
| 100 | 0,282 | 0,294 |
Основные физические свойства воды при различной температуре
| Температура | Плотность, ρ | Удельная теплоёмкость, Cp | Коэффициент температурного линейного расширения, α | Число Прандтля, Pr |
| оС | кг/м3 | кДж / (кг • К) | (1 / K) x 103 | — |
| 0 | 999,9 | 4,217 | -0,07 | 13,67 |
| 20 | 998,2 | 4,182 | 0,207 | 7,01 |
| 40 | 992,1 | 4,179 | 0,385 | 4,34 |
| 60 | 983,2 | 4,185 | 0,523 | 2,99 |
| 80 | 971,8 | 4,197 | 0,643 | 2,23 |
| 100 | 958,4 | 4,216 | 0,752 | 1,75 |
Температура кипения воды в зависимости от давления
1,013 бар
1,379 бар
2,068 бар
2,758 бар
3,585 бар
4,826 бар
6,205 бар
7,929 бар
10,34 бар
15,51 бар
Формулы физических свойств воды
При проведении инженерных расчетов удобнее использовать приближённые формулы для определения физических свойств воды⋆.
Плотность воды
⋆ [ кг/м3 ]
Теплоёмкость воды
⋆ [ Дж/(кг • К) ]
Теплопроводность воды
⋆ [ Вт/(м • K) ]
Динамическая вязкость воды
[ Па • c ]
Кинематическая вязкость воды
⋆ [ м2/с ]
Температуропроводность воды
⋆ [ м2/с ]
Число Прандтля воды
[ — ]
⋆ Приближённые формулы физических свойств воды получены авторами настоящего сайта.
Размерность величин: температура — К (Кельвин).
Приближённые формулы действительны в диапазоне температур воды от 283 К до 373 К.
Плотность пластовой нефти — Что такое Плотность пластовой нефти?
Плотность нефти (объемная масса) изменяется в пределах 730 — 1040 кг/м³.
На практике чаще используют единицы измерения г/см³ , плотность нефти изменяется в интервале 0,730 — 1,040 г/см³.
Более распространена нефть плотностью — 0,82-0,90 г/см³.
Классы плотности сырой нефти:
- супер легкая (super light) — до 0,78 г/см³ — выше 50оAPI — газовый конденсат;
- сверх легкая (extra light) — 0,78 — 0,82 г/см³ — 41,1- 50 оAPI;
- легкая (light) — 0,82- 0,87 г/см³ (light) — 31,1- 41,1оAPI;
- средняя (medium) — 0,87-0,92 г/см³ — 22,3-31,1оAPI;
- тяжелая — 0,92-1 г/см³ (heavy) — 10-22,3 оAPI;
- сверх тяжелая (extra heavy) — более 1 г/см³ — до 10 оAPI — битум.
Для нефти низкой плотности характерно:
- преобладание метановых углеводородов,
- низкое содержание смолисто — асфальтеновых компонентов,
- во фракционном отношении — высокое содержание бензиновых и керосиновых фракций.
Тяжелая нефть имеет повышенную концентрацию смолисто-асфальтеновых компонентов.
В США плотность нефти измеряется в градусах оAPI ( American Petroleum Institute (API), Американский институт нефти): высокие значения API соответствуют низким значениям плотности нефти.
Для характеристики нефти, как правило, используют величины относительной плотности.
Относительная плотность P – это безразмерная величина, численно равная отношению массы нефти (mнt) при температуре определения к массе дистиллированной воды при 40С (mвt), взятой в том же объеме:
Pt4 = mнt / (mвt)
Поскольку плотность воды при 40С равна 1, то численное значение абсолютной плотности и относительной совпадают.
Наряду с плотностью в нефтехимии существует понятие относительного удельного веса (Ɣ). Относительным удельным весом называется отношение веса нефтепродукта при температуре определения к весу дистиллированной воды при 4оС в том же объеме.
При одной и той же температуре плотность и удельный вес численно равны друг другу.
В соответствии с ГОСТом в РФ принято определять плотность и удельный вес при температурах 15 и 200 С.
Плотность нефти можно определить следующими методами:
- определение ареометром;
- гидростатическими весами Вестфаля-Мора;
- пикнометром;
- расчетным методом.
По плотности можно оценить состав и качество сырой нефти, поскольку ее значение для углеводородов различных групп различно:
- более высокая плотность — большее содержание ароматических углеводородов,
- средняя плотность — нафтеновая группа,
- более низкая — большее содержание парафиновых углеводородов.
Чем меньше плотность сырой нефти, тем легче процесс ее переработки нефти и выше качество получаемых нефтепродуктов.
Плотность нефти снижается с увеличением глубины залегания продуктивного пласта.
Плотность пластовой нефти — это масса нефти, извлеченной из недр с сохранением пластовых условий, в единице объема.
Обычно она в 1,2 — 1,8 раза меньше плотности дегазированной нефти, что объясняется увеличением ее объема в пластовых условиях за счет растворенного газа.
Известна нефть, плотность которой в пласте составляет всего 0,3 — 0,4 г/см3.
Ее значения в пластовых условиях могут достигать 1,0 г/см3.
По плотности пластовые нефти делятся на:
- легкие с плотностью менее 0,850 г/см3;
- тяжелые с плотностью более 0,850 г/см3.
Легкие нефти характеризуются высоким газосодержанием, тяжелые — низким.
Зависимость плотности жидкости от температуры и давления
Эксперянентально установлена линейная зависимость плотности ЖИДКОСТИ (р, г/см ) от температуры при данном давлении, описываемая уравнением [c.93]
Плотность жидкости изменяется при изменении температуры и давления. Зависимость плотности воды от температуры приведена в табл. 2. [c.8]
Газообразные жидкости имеют меньшую плотность по сравнению с капельными, при этом имеется сильная зависимость плотности от температуры и давления. [c.27]
Определение коэффициента Генри и коэффициента активности. Из уравнения (I, 77) следует, что методом газовой хроматографии можно определить константу равновесия вещества между газовой фазой и раствором в практически нелетучей жидкости. При этом для неподвижной жидкости нужно иметь данные о плотности и зависимости ее от температуры. Анализ следует проводить при строго постоянных температуре и давлении и точно измерять времена удерживания tm и /0. [c.205]
Изменение давления до 10 МПа мало влияет на изменение вязкости. При больших давлениях его влиянием на изменение вязкости пренебрегать нельзя. Аналитические зависимости вязкости от температуры весьма разнообразны. Отношение коэффициента динамической вязкости к плотности жидкости называется коэффициентом кинематической вязкости, который обычно и применяется в практических расчетах [c.18]
Третья величина молярный объем жидкости при ее давлении пара, может быть найдена несколькими различными способами. Вблизи комнатной температуры плотность жидкости и ее температурный коэффициент обычно довольно хорошо известны. Если критическая температура и плотность известны, то можно воспользоваться следующим уравнением, которое передает довольно точно зависимость плотности от температуры [19] [c.451]
Жидкости. У неполярных жидкостей между молекулами действуют практически только силы дисперсии. Диэлектрическая проницаемость с изменением температуры и давления изменяется мало, причем эта зависимость определяется зависимостью плотности от температуры. Для таких жидкостей дисперсия наблюдается до области оптических частот. Уравнение Максвелла (V.15) выполняется очень точно. [c.254]
Результаты, полученные Б. Б. Кудрявцевым [16], показывают, что измерение скорости звука в жидкостях может служить методом изучения силового поля молекул. Кудрявцев [15, 16] показал, что, измеряя зависимость между скоростью звука и молекулярным объемом жидкости при постоянной температуре, можно определить внутреннее давление жидкости. Автор отмечает, что приближенно те же вычисления можно произвести, если известны зависимость скорости звука и плотности жидкости от температуры. Акустические измерения в жидкостях, но мнению Б. Б. Кудрявцева, можно использовать для вычисления постоянной а в уравнении Ван-дер-Ваальса и зависимости этой величины от температуры. [c.452]
Некоторые исследователи [46, 103, 104] установили важную зависимость вязкости жидкостей и газов от плотности. Эта зависимость интересна потому, что дает возможность обоба е-ния данных по вязкости газов и жидкостей при различных температурах и давлениях. Особенность этой закономерности состоит в том, что если на одну из осей координат откладывать плотность р, а на другую—значение избыточной вязкости (ч1р.т — т), то экспериментальные данные для всех температур расположатся на одной кривой. [c.105]
На рис. I. 1.1—I. 1.29 приведены кривые, характеризующие плотности при различных температурах сжиженных газов под давлением собственных паров и жидкостей. В некоторых случаях приведены эмпирические уравнения, выражающие с достаточной для практических целей точностью зависимость плотности от температуры. [c.9]
Метод Уотсона [145] для нахождения зависимости плотности от температуры основан на применении безразмерного коэффициента расширения , обозначенного через св, который приблизительно одинаков для всех жидкостей при одних и тех же приведенных температуре и давлении. [c.452]
Согласно третьему закону термодинамики энтропия жидкой фазы, так же как и твердой, при абсолютном нуле температуры должна обращаться в нуль. В связи с этим приобретает большой интерес вопрос о распределении атомов в жидком гелии, особенно при наиболее низких температурах. Плотность жидкого гелия мала, под давлением насыщенных паров она составляет всего около 0,14 г/мл, что в значительной мере объясняется малой молекулярной массой гелия (заметим, что плотность жидкого водорода примерно в два раза меньше плотности жидкого гелия). Необычна зависимость плотности Не от температуры (рис. 61). Там же представлена температурная зависимость теплоемкости С вдоль линии равновесия жидкость — пар. При температуре 2,173 К и 49,80 10 Па плотность жидкого Не проходит через максимум, после чего функция р = /(Г) резко меняет свое направление, плотность быстро уменьшается. Теплоемкость тоже аномально зависит от температуры. Кривая теплоемкости похожа на греческую букву X. При 2,182 К теплоемкость является разрывной функцией. Здесь в жидком Не происходит фазовый переход второго рода. Температура этого фазового перехода ( Х-точки ) немного снижается при увеличении давления. Жидкую фазу при температурах, соответствующих Х-точкам и ниже, принято называть гелий II . Жидкая фаза при температурах, лежащих выше Х-точек, названа гелий 1 . [c.229]
Определяют физические параметры сжиженного газа в зависимости от его химического состава (плотность в зависимости от колебания температуры жидкости в трубопроводе вязкость в зависимости от температуры давление насыщенных паров при максимальной температуре). Плотность сжиженного газа определяется исходя из заданного состава и температуры в газопроводе. Температуру в газопроводе на каком-то расстоянии х от его начала определяют по формуле Шухова [c.468]
При измерении давления высотой столба жидкости, необходимо учитывать изменение объема (плотности) жидкости в приборе в зависимости от температуры. При отклонении температуры жидкости в приборе от О °С на показания прибора следует вводить поправку. [c.13]
Зависимость нижнего допустимого предела давления от температуры — причина основного отличия расчета транспортирования легкоки-пящих жидкостей от транспортирования нефти или воды. Поэтому определение закона изменения температуры перекачиваемой среды при гидравлическом расчете трубопровода необходимо не только для расчета физических свойств, в частности, плотности, перекачиваемой среды, но и для оценки перепада давления. При перекачке жидкости распределение температуры по длине трубопровода определяют по формуле Шухова [c.175]
Сложность приведенного выше условия кроется в одновременной зависимости плотности как от температуры, так и от давления, т. е. в данном случае р = p(i, р). Однако если плотность рассматриваемой жидкости слабо зависит от давления либо толщина жидкого слоя по вертикали очень мала, как это имеет место в тонком горизонтальном слое жидкости, то для построения разумной аппроксимации имеет смысл рассмотреть более простые критерии возможной неустойчивости. Так, например, в очень тонком горизонтальном слое, граничные поверхности которого поддерживаются при разных температурах, различия плотности р в вертикальном направлении оказываются обусловленными исключительно различием температур в разных точках слоя. Иначе говоря, влияние давления в этом случае очень слабое и хорошей аппроксимацией служит зависимость вида р = = p(t). Для состояний жидкости, при которых [c.202]
Этими номограммами можно пользоваться для газов, для жидкостей, а также для твердых тел (независимо от температуры и давления). При этом в случае пересчета концентрации газов из весовых процентов в г-мол/л (приложение II, номограмма 2), необходимо плотность газов брать при тех давлении и температуре, для которых ведется подсчет. Плотность (р) должна быть выражена в г1см если же она выражена как вес I л в граммах, то соответственно этому отсчет показаний на шкале Ла следует разделить на 1 ООО. Для подсчета плотности газов в зависимости от их температуры н давления приводится номограмма 5 (приложение П), позволяющая избежать при этом длительных арифметических вычислений. Номограмма 6 (приложение II) дает возможность производить пересчет объемных [c.39]
Высокие давления существенно влияют на температурную зависимость вязкости жидкостей. Из измерений вязкости воды при давлениях до 3,5-10 кгс-см- и температурах до 560 °С [18] было установлено, что температурный коэффициент вязкости отрицательный, если плотность превышает 0,8 г/см , и положительный, если плотность ниже этой величины эти экспериментальные данные примерно на 25% отличаются от значений, вычисленных на основе статистической теории твердых сферических молекул. [c.121]
Определение точки кипения в вакууме труднее, чем при атмосферном давлении, по трем основным причинам. Во-первых, при пониженном давлении труднее избежать перегревания кипящей жидкости. Во-вторых, зависимость точки кипения от давления при 15 мм больше, чем при давлении 760 мм. В-третьих, при обычном включении манометра измеряется не то дав.ление, которое существует около шарика термометра, а значительно меньшее, так как плотность паров кипящей жидкости отличается от плотности разреженного воздуха при комнатной температуре. Влияние двух первых причин можно в значительной степени устранить, влияние третьей — только частично. [c.114]
Для перехода от этих опытных данных к величинам парциальных упругостей и мы должны знать молекулярный вес частиц обоих тел. Поэтому, если одна из жидкостей смеси образует пары ненормальной плотности, т. е. переменного молекулярного веса, то для возможности применения методов перегонки мы должны заранее установить зависимость плотности пара от температуры и давления, другими словами — предварительно детально изучить явления диссоциации паров чистой жидкости в различных условиях давления и температуры. [c.274]
В начале опыта жидкость, отвешенную в маленькой, целиком заполненной ампуле, вводят в трубку 4 снизу через ванну со ртутью. Затем в муфту пропускают пар через трубку 2. Жидкость, пары которой пропускают, выбирают в зависимости от требуемой температуры. При нагревании ампула разрывается и пары вытесняют некоторый объем ртути из трубки 4. Так как пар анализируемого вещества находится в трубке под давлением меньшим, чем атмосферное, температура в муфте может не превышать температуры кипения вещества. Температуру паров в трубке 4 принимают равной температуре кипения нагревающей жидкости. Объем пара отсчитывают по делениям яа трубке 4 с учетом расширения стекла. Давление определяют вычитанием высоты столба ртути из барометрического с учетом поправок на расширение стекла трубки 4, изменение плотности ртути с температурой и на давление паров ртути . Метод при- [c.166]
Плотность жидкости с изменением давления практически не меняется (в расчетах этим изменением пренебрегают). Температура газов, находящихся в замкнутом пространстве и образующих двухфазную систему (в случае сжиженных газов), также мало влияет на изменение плотности жидкой фазы, но зато сильно влияет на плотность насыщенного пара (паровой фазы). Зависимость плотности насыщенных жидкостей и паров в замкнутом пространстве от температуры показана на рис. 1, 2 и 3. [c.12]
Плотность жидкости определяли с помощью пикнометров по ГОСТ 3900-47. Вязкость жидкости определяли в капиллярных вискозиметрах истечения по ГОСТ 33-66. Зависимость давления паров кеталей от температуры изучали динамическим методом [2]. Экспериментальные данные подвергали статистической обработке по методу наименьших квадратов. [c.51]
Калибровка пьезометра осуществлялась чистым жидким азотом при температуре 90,25° К. Количество жидкого азота в объеме пьезометра определялось измерением объема газообразного азота, полученного после испарения жидкости из пьезометра в измерительную систему. Зависимость плотности чистого жидкого азота от давления была взята по данным работы [6]. Калибровка пьезометра проводилась при рабочей температуре. Это исключало необходимость внесения поправки на изменение объема пьезометра изменением температуры. Учитывая [c.181]
Как указывалось выше, значения физических свойств жидкости, входящих в расчетные формулы, выбирают по определяющей температуре = 0,5 Т . + Гоо). Этот метод учета переменности физических свойств является приближенным. Он справедлив, если температура в пограничном слое меняется мало, а сами свойства в области этой температуры изменяются незначительно. При давлениях, близких к критическому (в области термодинамической критической точки), свойства жидкости изменяются сильно и немонотонно. Тогда метод определяющей температуры теряет силу. При этом уравнения пограничного слоя, записанные в приближении Буссинеска (в уравнении движения учитывается лишь зависимость плотности от температуры в слагаемом, определяющем массовую силу), необходимо обобщить на случай реальной зависимости свойств от температуры. Вследствие сложной зависимости физических свойств от температуры и давления теоретический расчет теплоотдачи проводится для конкретных жидкостей при фиксированных значениях давления, (или и Т о- Путем численного интегрирования системы уравнений пограничного слоя, записанных для переменных свойств жидкости, для Н2О, СО2, N2 и Не получена формула Попова—Янькова [c.225]
Кипение в большом объеме определяется как кипение па поверхности нагрева, погруженной в большой объем неподвижной жидкости. Эта жидкость может находиться нри ее точке кииеиия, и в этом случае говорят о кипении насыщенной жидкости в большом объеме или ниже ее точки кипения, когда говорят о кипении недогретой жидкости и большом объеме. Результаты исследования теплоотдачи при кипении в больы]ом объеме обычно представляются в внде зависимости плотности теплового потока от температуры поверхности стенки нагревателя Т ,, т. е. в виде кривой кипения. Кривая кипения воды прн атмосферном давлении показана на рис. 1. Возможно другое представлеиие с использованием перегрева стенки (Тщ,— вместо температуры стсики. [c.369]
Основные функциональные возможности ПИК интегрирование по времени частотных сигналов ТПР не менее чем одновременно по шести каналам (включая ТПР в БКН) аппроксимация градуировочных характеристик до пяти ТПР во всем рабочем диапазоне в виде функции К = Ф [ у) или К = Ф(/) с погрешностью не более 0,05 %, где/-частота выходного сигнала ТПР V — вязкость жидкости преобразование частотного сигнала плотномера 8сЬ1ишЬег ег 7835 в цифровой код автоматическая коррекция коэффициента преобразования ТПР в соответс вии с функциональной зависимостью К = = Ф [ у) или К = Ф(/) ручной ввод с клавиатуры значений плотности, избыточного давления в БИЛ и в БКН, температуры нефти (там же), влагосодержания, содержания солей магния (мг/л), содержания примесей (%) массы для осуществления вычислений при отсутствии или выходе приборов из строя, а также для определения массы нефти нетто ручной ввод с клавиатуры уставок предельных значений (нижнего и верхнего уровня расхода по каждой измерительной линии, верхнего и нижнего значений избыточного давления в БИЛ, верхнего и нижнего значений температуры в БИЛ (катушке К ), верхнего и нижнего значений плотности, разницы показаний плотномеров, нижнего и верхнего уровня избыточного давления в БКН, перепада давлений на блоках фильтров, нижнего уровня расхода в БКН, нижнего уровня температуры жидкости, содержание газа в нефти) вычисление мгновенного и мгновенного суммарного расходов по каждой линии и по установке в целом, соответственно сравнение показаний параллельно работающих плотномеров и выдачу данных расхождения вычисление средних значений плотности (при текущей температуре и 20 °С), температуры, давления, влажности партии перекачиваемой нефти с начала текущей смены, двухчасовки, относительной погрешности вычисления суммарного объема, массы брутто нефти, объемного расхода — не более 0,05 %. [c.70]
Поверхность теплообмена внутренней пленки обрабатываемой жидкости есть функция плотности жидкости, которая в свою очередь зависит от температуры. Удельная теплоемкость при постоянном давлении Ср также зависит от температуры. Эти зависимости, приведенные в табл. 7, использ овали при расчете на ЭВМ для решения уравнения (УП,40). Величины рассчитывали в области температур 50—110 °С с интервалом в 3 °С. Кроме того, на ЭВМ рассчитывали также критерии Рейнольдса, Прандтля и симплекс вязкости при этих температурах. Выход из второй ступени программы сохраняли на лентах и затем использовали как вход третьей ступени программы. [c.133]
Кривая зависимости давления пара от температуры имеет физический смысл лишь в определенной области давления и температуры. При увеличении температуры и давления плотности жидкости и пара начинают сближаться между собой по своему значению, и наконец достигается такое состояние, при котором жидкость и пар становятся неразличимыми по всем термодинамическим параметрам (например, по плотности и молярному объему), исчезает граница жидкость — пар, соответственно поверхностное натяжение становится равным нулю. Это состояние называется критическим. Энтальпия испарения с увеличением температуры понижается и в критическом состоянии также становится равной нулю. Соответствующая температура называется критической Гкрит (аналогично ркрит, Укрит, ркрит). В критическом состоянии пар и жидкость неразличимы. Нельзя считать, как это иногда делают, что критическое состояние отличается тем, что выше критических температуры и давления невозможно превратить газ (пар) в жидкость. Критическая плотность составляет примерно треть плотности жидкости в нормальных условиях, соответственно она в 300 раз больше плот- [c.276]
Двоякое поведение жидкой воды следует также из большого числа других экспериментальных данных. Так, зависимость плотности воды от температуры и понижение температуры максимальной плотности жидкости с возрастанием давления можно хорошо объяснить, если учесть возможность самоперехода объемной структуры воды в более плотную форму. Таким же образом вызываемые давлением разрушения объемной структуры с образованием в жидкости менее плотных компонентов можно объяснить влиянием температуры на вязкость воды, находящейся под высоким давлением [33]. Данные по поглощению ультразвука водой также согласуются с развитыми представлениями о пребывании воды в виде двух отличающихся по состоянию жидкостей. Минимум, наблюдаемый при 55° на кривой поляризуемость электрона — температура, объясняется термическим разрушением структурных пустот и степенью заполнения этих пустот ближайшими молекулами воды [35]. Кроме этого, близкие значения энергии активации диэлектрической релаксации, ламинарного потока и самодиффузии (4,6 ккал/люль) также позволяют предположить, что лимитирующей стадией для всех этих процессов является разрушение структуры [36]. Количественная обработка такого двойственного поведения воды дает возможность определить степень разрушения водородных связей, которая меняется в зависимости от выбранной модели от 0,1 до 70% при 0° [37]. Очевидно, эти величины относятся к различным моделям или к различным степеням разрушения водородных связей. Как следует из данных по дисперсии рентгеновских лучей, многие физические свойства воды, которые свидетельствуют о ее существовании в двух жидких состояниях, можно объяснить, используя существенно отличающиеся друг от друга модели [29, 38]. Следовательно, точное определение природы менее связанного плотного состояния воды представляет значительную трудность, [c.15]
На рис. VII. 9 приведена зависимость Рпр =/(7 пр), позволяющая приближенно установить температуру кипения жидкости и давления насыщенного пара, и их плотность по рис. VII. 10 К — критическая точка) Р = РпрРкр и р = рпрркр. [c.134]
Момент фазового перехода можно определить не только визуально, но и любыми методами, позволяющими установить зависимость изменения какого-либо свойства системы от изменения температуры, давления, объема и т. д. Например, введя в аппарат определенные количества лколичеств веществ, т. е. уменьшают объем системы. Отмечая на графике зависимость какого-либо из свойств системы или фазы (объема, плотности, коэффициента преломления и др.) от давления, легко заметить, что эта зависимость будет представлять собой плавную кривую до тех пор, пока не изменится число равновесно существующих фаз. В этот момент на кривой давление—свойство появится перелом. Давление, соответствующее этому перелому при растворении газа в жидкости, будет давлением, при котором исчезает последний пузырек газа. Аналогичные результаты можно получить, если повышать давление, вводя в аппарат дополнительные точно измеренные количества жидкости или газа. Зная исходный состав газовой фазы, можно, повышая давление в системе, определить момент выделения первой капли жидкости, т. е. определить точку росы. [c.288]
Вторая поправка. Когда вещество кипит, наблюдается градиент температуры между поверхностью жидкости и уровнем нагревателя. Этот градиент можно рассчитать из плотности жидкости и дaвJleния пара или измерить термопарой на разных глубинах жидкости. Кроме того, температура части стенки, погруженной в жидкость, уменьшается при снижении уровня жидкости. Наиболее важна величина, обусловленная градиентом температуры, изменявшаяся от 10 до 35 кал/моль в зависимости от наполнения испарителя, количества испаренного вещества и давления в опыте [13]. [c.12]
Влияние дарления на реологические свойства. Поскольку вязкость жидкости определяется величиной сил межмолекулярного взаимодействия (стр. 34—ЗЬ), которые передают момент количества движения, и поскольку эти силы существенно зависят от межмолекулярных расстояний можно предполагать, что сжатие жидкости должно сопровождаться существенным увеличением вязкости. Иногда это предположение подтверждается экспериментальными данными. Однако для большинства случаев изменение вязкости не слишком значительно, так как для того, чтобы изменить плотность на небольшую величину, следует приложить очень высокое давление. Так, вязкость этилового эфира или ацетона увеличивается при повышении давления до 4000 атм соответственно в 6,3 и 3,9 раза Однако у некоторых жидкостей наблюдается необычно сильное изменение вязкости. Например, вязкость изобутанола при давлении 12 ООО атм увеличивается в 790 раз по сравнению с его вязкостью при той же температуре, но при атмосферном давлении . У некоторых разновидностей силиконовых жидкостей — вязкость увеличивается в 10 раз даже при давлениях менее 10 ООО атм. Большой экспериментальный материал о зависимости вязкости обычных жидкостей от давления можно найти в работе Герси и Хопкинса . [c.47]
Вы делаете это неправильно: расчет глубины / Хабр
Приветствую вас, глубокоуважаемые!
Что если я скажу, что глубина, что бы вы под ней не подразумевали, является одной из самых сложных для точного измерения величин? На какой глубине плывет подводная лодка? Какая глубина марианской впадины? На какой глубине лежит Титаник? Если вам не повезет с параметрами, то на первом километре глубины, вы можете ошибиться примерно на 30-40 метров и на 200-300 метров на 6-ом километре, используя датчик давления. Если вы предпочитаете эхолот, то при неудачном стечении обстоятельств, которые вы не учли, ошибка на первом километре составит метров 100, а на 6-ом — целый километр. Конечно, можно еще использовать длинную веревку… Но там, как известно, свои подводные камни.
Как такое могло случиться и как делать правильно я расскажу под катом. В довесок к статье есть Open-source библиотека на C#/C/Rust/Matlab/Octave/JavaScript и пара онлайн-калькуляторов для демонстрации.
Статья будет полезна разработчикам подводной техники, число которых за последние лет пять выросло в разы.
Итак, для начала сразу оговоримся, что глубиной часто называют две разных величины:
- и расстояние по вертикали от поверхности воды до точки, где эту глубину измеряют,
- и расстояние по вертикали от поверхности воды до дна.
В первом случае — это
глубина погружения
, а во втором —
глубина места
.
Есть ровно два с половиной фундаментальных способа изменения этих величин, как я уже упомянул:
- по гидростатическому давлению столба жидкости, т.е. при помощи датчика давления;
- по времени распространения звука — эхолотом
- по длине выпущенной за борт веревки =)
С веревкой все понятно, а с остальными двумя давайте разберемся.2.
Давайте абстрагируемся от точности конкретных приборов, пусть даже они у нас суперточные.
Проблема в том, что никакой член формулы не является константой. Даже атмосферное давление может меняться в течение часа.
Как влияет атмосферное давление?
Давление у поверхности моря может
варьироваться в пределах 641-816 мм. рт. ст.
, или, тоже самое в миллибарах: от 855 до 1087. Если просто взять за
стандартное значение в 1013.25 мБар, то в зависимости от погоды уже можно получить ошибку в 40-50 сантиметров, причем, как в «плюс», так и в «минус».
Что с ускорением свободного падения?
Боюсь показаться Кэпом, но все же напомню, что земля у нас
плоская
вращается, и за счет центробежной силы притягивает на экваторе слабее, чем на полюсах.
Если не крохоборничать и не учитывать гравитационные аномалии из-за разной плотности земных пород, гор, впадин, изменения скорости вращения земли от сброшенной земными деревьями листвы и перемещениями соков по их стволам, то нас вполне устроит стандартная зависимость ускорения свободного падения от георафической широты. Т.н WGS-84 Gravity formula.
Согласно этой формуле, ускорение свободного падения меняется от 9.7803 м/с2 на экваторе (0° градусов широты) до 9.8322 м/с2 на полюсах (90/-90° широты).
Допустим, мы возьмем стандартное значение ускорения свободного падения 9.80665 м/с2, на сколько мы ошибемся в худшем случае?
Это иллюстрируетя картинкой ниже. На ней синий график показывает ошибку определения глубины на экваторе, если мы будем использовать стандартное значение , а оранжевый график — такую же ошибку на полюсах.
То есть, если мы подставим в формулу стандартное значение и пойдем погружаться где-то ближе к экватору, то на 100 метрах ошибемся всего на 20-30 сантиметров, на километре — на 2,5-3 метра, а на 9-10 километрах (Бездна Челленжера, кстати, находится на 11° северной широты) ошибка будет уже 25-30 метров. Т.е. реальная глубина будет больше, чем та, которую мы измерим.
А как влияет плотность воды?
Самым нехорошим образом. Если два первых компонента погрешности учесть достаточно просто, да и вклад их весьма скромен, то с плотностью воды история более замысловатая.
Дело в том, что плотность воды в упрощенном случае есть функция температуры, давления и солености.
То есть мало измерять давление, атмосферное давление, учитывать географическую широту места. Нужно еще знать температуру и соленость воды.
Для определения плотности морской воды в (разумном) диапазоне условий на практике наиболее широко применяется формула из работы Чена и Миллеро (Да, ЮНЕСКО занимается еще и этим!)
Допустим, мы измерили и температуру и соленость, но остается сжимаемость воды — изменение плотности с давлением (т.е. с глубиной), и чтобы определить высоту столба жидкости нужно просуммировать высоты элементарных столбиков, на которых давление изменяется на какую-то малую величину . В целом это конечно интеграл, но чтобы сразу привнести некое практическое значение, запишем его так:
N — это число интервалов разбиения давления от
до измеренного
.
Плотность зависит от давления практически линейно, и считать такую сумму из-за учета одной лишь сжимаемости смысла нет, но я привел здесь эту формулу не просто так.
Сам факт, что плотность зависит от трех параметров — это еще пол беды. Сложность кроется в том, что все эти параметры могут сильно меняться с глубиной. В этом случае принято говорить о профиле температуры и солености. Вот так, к примеру, выглядит профиль из Арктики:
Вот так с северной части тихого океана:
А вот так, для сравнения — с юга атлантики:
Например, если представить, что мы погружается в северной части тихого океана (39°СШ,152°ВД) учитываем атмосферное давление и географическую широту места и сжимаемость воды, а наш датчик давления показывает 100 Бар (~1000 м), а температуру и соленость мы берем в точке измерения, но не учитываем профиль, мы ошибемся с глубиной на 2 метра.
Я специально запилил онлайн-калькулятор и добавил три тестовых профиля (их можно переключать кнопками), чтобы каждый мог сам попробовать.
Если теперь просто переключить профиль на «южноатлантический» и попробовать пересчитать, то мы увидим, что разница выросла до 6-и метров. Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.
Естественно, все меняется и со сменой времен года и со сменой времени суток. Летом (в северном полушарии, зимой — в южном) верхний слой прогревается, а зимой — остывает. Шторма перемешивают воду, дожди смывают грязь с суши и реками уносят в моря, таят снега и ледники.
Это я к тому, что нельзя один раз перемерить и выбить в граните все профили температуры и солености для всех морей и океанов — все течет, все меняется. И если вдруг вы собрались погружаться на ощутимые глубины и у вас нет температурного профиля — я не поверю в ваш рекорд )
Матчасть
Как я упомянул в начале статьи, все необходимое для расчета глубины я собрал в библиотеку и
положил на GitHub
.
Она в том числе переведена на JavaScript, а в качестве интерактивного примера ее использования привожу онлайн-калькулятор.
P.S.
Благодарю за внимание, буду искренне благодарен за конструктивную критику, сообщения об ошибках, пожелания и предложения.
В следующей статье разберу второй способ определения глубины — по эхолокации.
Глава 4.1. Свойства воды | BookOnLime
Описание свойств воды начинают, обычно, с характеристики аномалий, присущих воде – самому распространенному и, вместе с тем, самому загадочному и необычному веществу на земле. Причем практически каждое из этих аномальных свойств имеет важное значение для обеспечения жизнедеятельности на земле. Необычные свойства воды особенно ярко выделяются на фоне свойств ее гомологов: h3S, h3Se, h3Te. Молекула воды является самым первым и легким представителем этого гомологического ряда, однако гидриды серы, селена и теллура при комнатной температуре, в отличие от воды, находятся в газообразном состоянии (рис. 23).
И вода, если бы она была обычным членом гомологического ряда, должна в соответствии со своей молекулярной массой закипать при температуре –70 оС и превращаться в лед при температуре –90 оС, а значит, не могла бы быть основой жизни на земле.
Рис. 23. Точки плавления и кипения гидридов VI группы Периодической системы элементов
Другая особенность воды – это аномальное изменение плотности в зависимости от температуры (рис. 24). В обычных жидкостях плотность всегда уменьшается с ростом температуры. Для воды характер изменения плотности в зависимости от температуры другой – после таяния льда плотность увеличивается, проходит через максимум при температуре 4 оС, а затем уменьшается с ростом температуры.
Рис. 24. Зависимость плотности воды от температуры
Жидкая вода имеет максимум плотности не в точке плавления, а при температуре 4 оС и ее плотность уменьшается, как при повышении температуры, так и при ее понижении до температуры возможного переохлаждения, равной – 40 оС (при 1 атмосфере). При этом плотность воды больше плотности льда на 10%, благодаря чему лед плавает на поверхности воды. При температуре 4 оС вода уменьшается в объеме до минимальных значений, а при дальнейшем понижении температуры от 4 оС до 0 оС расширяется (рис. 25).
Рис. 25. Зависимость молярного объема воды и льда от температуры
Минимум объема воды при температуре 4 оС обусловлен, по мнению Зацепиной Г.Н., особенностью межмолекулярного взаимодействия системы Н2О, в которой число межмолекулярных переходов протонов равно числу внутримолекулярных переходов. Вода, превращаясь в лед, благодаря увеличению объема приобретает огромную силу, способность разрушать крепчайшие породы и, вместе с тем это спасает нашу планету от оледенения. Так как максимум плотности при 4 оС предотвращает конвективное перемешивание жидкости и опускание на дно поверхностных слоев воды, остывших до температуры ниже 4 оС, что замедляет дальнейшее охлаждение и промерзание водоемов.
Морская вода, в отличие от пресной ведет себя иначе. Наличие различных солей меняет ее физико-химические свойства. Она замерзает при – 1,9 оС (переохлажденная вода) и имеет максимальную плотность при – 3,5 оС, то есть она превращается в лед, не достигая наибольшей плотности. Переохлажденная вода, то есть остающаяся в жидком состоянии ниже точки замерзания 0 оС, ведет себя странно, с одной стороны плотность воды сильно уменьшается по мере переохлаждения, но, с другой стороны она приближается к плотности льда при понижении температуры.
Другая аномалия воды – необычное поведение ее сжимаемости, то есть уменьшение объема при увеличении давления. Для обычных жидкостей сжимаемость растет с температурой – при высоких температурах жидкости более рыхлы, имеют меньшую плотность, их легче сжать. Вода так ведет себя при высоких температурах выше 50 оС. При низких температурах, от 0 оС до 45 оС сжимаемость воды меняется противоположным образом, в результате при температуре 45 оС появляется минимум. Изотермическая сжимаемость воды при температуре 0 оС в четыре раза больше, чем изотермическая сжимаемость льда (рис. 26).
Рис. 26. Зависимость сжимаемости воды от температуры
Максимальное изменение сжимаемость испытывает при плавлении. Сжимаемость воды и льда мала по сравнению со сжимаемостью других веществ (табл.4.1.1).
Таблица 4.1.1. Сжимаемость ряда веществ в интервале температур от 5 оС до 30 оС
Температура, оС | βs ·1012, дин/см2 | ||
Вода | Метанол | Бензин | |
5 | 51,6 | – | 84,2 |
10 | 48,7 | 114,9 | 88,5 |
15 | – | 118,8 | 92,2 |
25 | 46,6 | 122,7 | 95,6 |
30 | 45,8 | 131,0 | 103,1 |
Указание особенности изменения сжимаемости воды и льда объясняют характером водородных связей в них. На этих примерах видно, что необычные свойства воды характеризуются появлением максимумов или минимумов на кривых зависимостей от температуры. Такие зависимости означают, что имеют место два противоположных процесса, которые и определяют эти свойства. Один процесс – это обычное тепловое движение, которое усиливается с ростом температуры и делает воду, как и любую другую жидкость, более разупорядоченной. Другой процесс необычный, присущий только воде, за счет него вода становится более упорядоченной при низких температурах. Разные свойства воды по-разному чувствительны к этим двум процессам, и поэтому положение экстремума наблюдается для каждого свойства при своей температуре.
Самая сильная аномалия воды – это температурная зависимость ее теплоемкости. Величина теплоемкости показывает, сколько нужно затратить тепла, чтобы поднять температуру вещества на один градус. При нагревании вещества теплоемкость, как правило, возрастает для всех веществ, кроме воды. Изменение теплоемкости воды с повышением температуры аномально – от 0 оС до 37 оС она падает и от 37 оС до 100 оС начинает повышаться. Теплоемкость водяного пара приближается к теплоемкости льда. Минимальное значение теплоемкость воды имеет около 37 оС. Это нормальная температура тела человека (36,6–37 оС), именно при этой температуре происходят сложные биохимические процессы в организме человека, значит энергетически это наиболее выгодные условия. Для подавляющего числа веществ теплоемкость жидкости после плавления кристалла изменяется незначительно (табл. 4.1.2).
Таблица 4.1.2. Теплоемкость веществ в трех агрегатных состояниях
Агрегатное состояние | Теплоемкость вещества (СоР, кал/моль) | ||||||
Н2О | Nh4 | Ch5 | HCl | h3 | Hg | Na | |
газообразное | 8,75 | 9,9 | – | 6,7 | 6,9 | – | 5,0 |
жидкое | 18,0 | 12,0 | 11,0 | 12,0 | 11,0 | 6,8 | 7,6 |
твердое | 9,0 | 9,0 | 14,0 | 15,0 | 13,0 | 6,7 | 8,0 |
Вода же при плавлении льда меняет теплоемкость в два раза, такого огромного скачка при плавлении не наблюдается ни у одного вещества. Теплоемкость льда имеет очень низкое значение, она близка к теплоемкости одноатомных кристаллов и равна теплоемкости твердого аммиака. В процессе плавления металлов теплоемкость практически не изменяется, для веществ из многоатомных молекул в процессе плавления она, как правило, уменьшается, что, вероятно, связано с тем, что молекулы могут свободно вращаться в жидкости, и не могут в твердом теле. Для таких соединений как Н2О и Nh4 теплоемкость в жидком состоянии много больше, чем в твердом состоянии. Это означает, что в воде открываются какие-то новые, энергоемкие процессы, на которые тратится подводимое тепло, что и обуславливает появление избыточной теплоемкости, причем это характерно для всего диапазона температур, при которых вода находится в жидком состоянии. Эта аномалия исчезает только в паре, то есть это свойство именно жидкой воды. Для переохлажденной воды теплоемкость еще больше возрастает при сильном переохлаждении, то есть переохлажденная вода еще более аномальна, чем обычная. Высокая теплоемкость воды и высокая удельная теплота плавления среди простых веществ (лед трудно растопить, а воду заморозить) способствуют смягчению климата на земле, не происходит резкого перепада температур зимой и летом, ночью и днем, поскольку существует гигантский регулятор, своеобразный термостат – воды Мирового океана.
Другой величиной, которая определяет характер теплового движения в жидкостях, является теплопроводность. Зависимость изменения теплопроводности воды от температуры приведена на рисунке 26. Для сравнения приведено изменение теплопроводности четыреххлористого углерода, который ведет себя, как обычная жидкость, то есть с ростом температуры уменьшается теплопроводность и растет теплоемкость. Как видно из рисунка 27, теплопроводность при плавлении льда уменьшается приблизительно в четыре раза. Переохлажденная вода имеет тот же характер изменения теплопроводности, что и обычная.
Рис. 27. Зависимость теплопроводности воды и четыреххлористого углерода от температуры
Все нормальные жидкости с ростом давления изменяют знак зависимости теплопроводности от температуры. Теплопроводность воды не изменяет характера температурной зависимости под давлением. Относительная величина увеличения теплопроводности воды при давлении 1200 кг/см2 составляет около 50%, в то время как для нормальных жидкостей это увеличение при том же давлении составляет приблизительно 270%. Теплопроводность воды слабо зависит от давления, что связано с малой сжимаемостью воды по сравнению с другими жидкостями.
И, наконец, еще одно удивительное свойство воды, связанное с особенностями ее поверхностного натяжения. Вода в свободном состоянии принимает шарообразную форму (капли дождя, росы). На границе двух сред (вода-воздух) силы межмолекулярного притяжения действуют с одной стороны, стягивая поверхность жидкости. На структуру поверхностного слоя воды влияет два фактора – полярность молекул воды и сетка водородных связей. Поверхностное натяжение воды 72 мн/м (миллиньютон/метр). Это поверхностное натяжение настолько велико, что смоченные водой две пластинки из стекла удается разъединить только с помощью огромных усилий. Из всех известных жидкостей силы поверхностного натяжения воды по своей величине уступают только ртути (около 500 мн/м).
Рис. 28. Зависимость сдвиговой вязкости от температуры для воды и четыреххлористого углерода
Еще одно аномальное свойство воды – ее вязкость. Обычные жидкости с повышением давления увеличивают вязкость, а с ростом температуры уменьшают. Характер изменения вязкости у воды другой. На рисунке 28 представлена зависимость вязкости от температуры для воды и четыреххлористого углерода. Как видно из рисунка вязкость четыреххлористого углерода до температуры около 23 оС меньше, чем у воды, а для больших температур она больше, чем у воды.
Зависимость вязкости от давления для разных температур приведена на рисунке 29, из которой следует, что для низких температур с ростом давления вплоть до 2000 атм вязкость воды уменьшается, а затем начинает расти и при температуре 100 оС кривая близка по характеру зависимости для обычных жидкостей.
Рис. 29. Зависимость сдвиговой вязкости от давления для ряда температур
Увеличение вязкости для них с ростом давления связано с уменьшением длины свободного пробега молекул, так как при большем давлении они плотнее упакованы. Как видно из приведенных характеристик, вода действительно является необычной, аномальной жидкостью и природа этих аномалий кроется в особенностях ее структуры.
Плотность жидкостей в зависимости от давления и изменения температуры
Плотность жидкости изменяется в зависимости от температуры и давления. Плотность воды в зависимости от температуры и давления указана ниже:
См. Также «Вода — плотность, удельный вес и коэффициент теплового расширения», онлайн-калькулятор, рисунки и таблицы, показывающие изменения в зависимости от температуры.
Плотность
Плотность жидкости может быть выражена как
ρ = м / В (1)
, где
ρ = плотность жидкости (кг / м 3 )
m = масса жидкости (кг)
V = объем жидкости (м 3 )
Плотность, обратная удельному объему:
v = 1 / ρ
= В / м (2)
, где
v = удельный объем (м 3 / кг)
Объем и изменение температуры
При повышении температуры — большая часть жидкостей расширяется:
dV = V 1 — V 0
= V 0 β dt
= V 0 β (t 1 — t 0 ) (3)
, где
dV = V 1 — V 0 = изменение объема — разница между конечным и начальным объемом (м 3 )
β = коэффициент объемного температурного расширения (m 3 / m 3 o C)
dt = t 1 — t 0 = изменение температуры — разница между конечной и начальной температурой ( o C)
( 3) можно изменить на
V 1 = V 0 (1 + β (t 1 — t 0 )) (3b)
Плотность и изменение температуры
Для (1) и (3b) конечная плотность после изменения температуры может быть выражена как
ρ 1 = m / ( V 0 (1 + β (t 900 62 1 — t 0 ))) (4)
где
ρ 1 = конечная плотность (кг / м 3 )
— или в сочетании с (2)
ρ 1 = ρ 0 / (1 + β (t 1 — t 0 )) (4b )
где
ρ 0 = начальная плотность (кг / м 3 )
Объемные температурные коэффициенты
β
Примечание! — объемные температурные коэффициенты могут сильно изменяться в зависимости от температуры.
Плотность и изменение давления
Влияние давления на объем жидкости можно выразить с помощью трехмерного закона Гука
E = — dp / (dV / V 0 )
= — (p 1 — p 0 ) / ((V 1 — V 0 ) / V 0 ) (5)
где
E = модуль объемной упругости — эластичность жидкости (Н / м 2 )
Знак минус соответствует тому, что увеличение давления приводит к уменьшению объема.
С (5) — конечный объем после изменения давления может быть выражен как
V 1 = V 0 (1 — (p 1 — p 0 ) / E) (5b )
Объединение (5b) с (1) — конечная плотность может быть выражена как:
ρ 1 = m / ( V 0 (1 — (p ) 1 — p 0 ) / E)) (6)
— или в сочетании с (2) — конечная плотность может быть выражена как
ρ 1 = ρ 0 / (1 — (p 1 — p 0 ) / E) (6b)
Объемный модуль упругости жидкости некоторые распространенные жидкости —
E 9 0240
- вода: 2.15 10 9 (Н / м 2 )
- этиловый спирт: 1,06 10 9 (Н / м 2 )
- масло: 1,5 10 9 (Н / м 2 )
Примечание! Модуль объемной упругости жидкостей зависит от давления и температуры.
Модуль объемной упругости для воды — британские единицы
Модуль объемной упругости для воды — единицы СИ
Плотность жидкости, изменяющая температуру и давление
Плотность жидкости при изменении температуры и давления может быть выражена как сочетание (4b) и (6b) :
ρ 1 = ρ 1 (из ур.1) / (1 — (p 1 — p 0 ) / E)
= ρ 0 / (1 + β (t 1 — t 0 )) / (1 — (p 1 — p 0 ) / E) (7)
Пример — плотность воды при 100 бар и 20
o C
- плотность воды 0 o C : 999,8 (кг / м 3 )
- Коэффициент расширения воды при 10 o C : 0.000088 ( м 3 / м 3 o C) (среднее значение от 0 до 20 o C)
- модуль объемной упругости воды: 2,15 10 9 (Н / м 2 )
Плотность воды можно рассчитать по (3):
ρ 1 = (999,8 кг / м 3 ) / (1 + (0,000088 м 3 / м 3 o C) ((20 o C) — (0 o C) )) / (1 — ((100 10 5 Па) — (1 10 5 Па) ) / ( 2.15 10 9 Н / м 2 ) )
= 1002,7 (кг / м 3 )
Калькулятор плотности воды | Будет ли он плавать или тонуть?
С помощью этого калькулятора плотности воды вы можете быстро оценить плотность соленой воды. В этом тексте вы найдете ответ на вопрос «Какова плотность воды?» И как она изменяется в зависимости от температуры, солености или давления. Вы когда-нибудь задумывались, какая связь между плотностью воды в кг / м³ , плотностью воды в г / мл и плотностью воды в фунтах / фут³ ? Должны ли яйца плавать или тонуть в соленой воде? Читайте также, чтобы найти ответы на эти вопросы!
Какая плотность воды?
Плотность воды (или любого другого вещества) определяется как отношение ее массы, м , к ее объему, V .Плотность обычно обозначается с помощью символа ρ , поэтому формула для плотности:
ρ = м / В .
Оказывается, что плотность для большинства веществ непостоянна, но фактически изменяется при изменении внешних параметров, таких как температура или давление.
Единицы измерения плотности воды
Есть разные единицы плотности воды. На самом деле допустима любая комбинация единиц массы и единиц объема, но некоторые из них более распространены, чем другие.Наиболее часто используемые единицы:
- [кг / м³] — килограмм на кубический метр,
- [фунт / фут³] — фунт на кубический фут,
- [г / мл] или [г / см³] — грамм на миллилитр или грамм на кубический сантиметр, которые эквивалентны друг другу.
Плотность воды в кг / м³ в 1000 раз больше, чем плотность воды в г / см³ и примерно в 16,018 раз меньше, чем плотность воды в фунт / фут³ .Если вас интересуют различные единицы измерения плотности и вы хотите знать взаимосвязь между ними, попробуйте наш конвертер плотности.
Температурная зависимость плотности воды
Вы, вероятно, знаете о феномене изменения плотности воды при разных температурах, даже если вы никогда не задумывались об этом с научной точки зрения; когда-нибудь задумывался, почему плывет лед? Это изменение в основном вызвано тепловым расширением — при повышении температуры одно и то же количество вещества занимает все больше и больше места. В результате масса остается постоянной, но объем увеличивается, вызывая уменьшение плотности .
Качественно это довольно просто, но с математической точки зрения оценка результата — совсем другое дело. У воды есть интригующее свойство — она достигает максимальной плотности примерно при 4 ° C или 40 ° F . Хотя существуют таблицы плотности чистой воды между точкой замерзания воды ( 0 ° C или 32 ° F ) и ее точкой кипения ( 100 ° C или 212 ° F ), простой формулы не существует. что дает точное значение для данной температуры.Чтобы обойти это, наш калькулятор плотности воды использует приближенное уравнение, основанное на полиноме 5-го порядка:
ρ (T) = ρ₀ + a₁ * T + a₂ * T² + a₃ * T³ + a₄ * T⁴ + a₅ * T⁵ ,
, где температура T находится в ° C , а значения коэффициентов следующие:
-
ρ₀ = 999,83311 кг / м³, -
a₁ = 0,0752 кг / (м³ · ° C), -
a₂ = -0,0089 кг / (м³ · ° C²), -
a₃ = 7.36413 * 10⁻⁵ кг / (м³ · ° C³), -
a₄ = 4,74639 * 10⁻⁷ кг / (м³ · ° C⁴), -
a₅ = 1,34888 * 10⁻⁹ кг / (м³ · ° C⁵),
Мы используем научную нотацию для более четкого выражения всех малых значений. Хотя результат является приблизительным, он предоставляется с достаточной точностью.
Плотность соленой воды
Смесь воды и соли, далее именуемая соленой водой, имеет плотность, отличную от плотности чистой воды. Основной параметр, который говорит нам о количестве соли в соленой воде, — это соленость, S , выражаемая как:
S = m₁ / (m₁ + m₀) ,
, где м₀ — масса чистой воды, а м₁ — масса соли.Другими словами, смешивание массы чистой воды м₀ с массой соли м₁ дает соленую воду с соленостью S . Это количество обычно указывается в промилле ‰ , частях на тысячу (ppt) или практических единицах солености (psu), которые в основном эквивалентны.
В нашем калькуляторе плотности воды мы используем метод, предложенный Миллеро и его коллегами. Общая формула сложна, поэтому мы не будем показывать ее здесь явно, но, как правило, в ней используется та же концепция, что и в уравнении для температурной зависимости плотности — полином, состоящий из смешанных членов температуры, солености и давления:
ρ (T, S, p) = ρ (T) + f (T, S, p) .
Здесь ρ (T) — плотность чистой воды, полученная в предыдущей главе.
Однако мы можем выделить некоторые общие свойства — плотность соленой воды увеличивается с увеличением солености и более высоким внешним давлением .
Как пользоваться калькулятором плотности воды?
Какова плотность воды при 20 ° C солености S = 35 ‰ и под давлением 1 атм ? Давайте попробуем наш калькулятор плотности воды и узнаем!
- Установить температуру
20 ° C. - Установите соленость на
35 ‰. - Установить давление на
1 атм. - И все! Плотность соленой воды
1024,9 кг / м³.
Такая же плотность воды составляет 1,0249 г / мл , или 63,982 фунта / фут³ .
Но это еще не конец! Проведите собственный эксперимент дома — возьмите несколько предметов с неизвестной плотностью (но более или менее равной значению плотности воды, например, 1000 кг / м³ ).Хотя изменить внешнее давление не так просто, вы можете создать жидкость с известной соленостью и контролировать ее температуру. Ознакомьтесь с расширенным режимом , чтобы узнать, сколько чистой воды и соли необходимо для получения соленой воды с определенной плотностью .
Вы можете начать с нагрева смеси (например, в микроволновой печи), а затем погрузить в нее свои предметы. Вы можете быстро оценить температуру воды, пока она остывает. Вначале плотность горячей воды довольно высока, поэтому все должно утонуть, но в какой-то момент плотность уменьшится до такой степени, что объект начнет плавать! Вставьте значение солености и температуры, при которых объект начал плавать, в калькулятор плотности воды, и вы сможете оценить эти плотности с относительно хорошей точностью!
Вы также можете выбрать один из объектов из списка, чтобы увидеть, плавает он или тонет.Мы принимаем во внимание некоторые средние значения, поэтому результаты могут быть не точными в каждом случае (особенно для фруктов).
Должны яйца плавать или тонуть?
Что ж, самый точный ответ: это зависит от обстоятельств!
Во-первых, есть разница между свежими и тухлыми яйцами. Если вы хотите сварить яйцо, его можно опустить в чистую теплую воду, прежде чем проверять, открывая. Если он тонет, он должен быть свежим, а если плавает, скорее всего, несвежий. По мере того как яйцо стареет, внутри выделяются некоторые газы (например, сероводород), которые выходят из объекта через поры в скорлупе.В результате масса уменьшается, но объем яйца остается постоянным, поэтому плотность уменьшается.
Второй фактор — это соленость воды. Когда мы готовим, мы чаще всего используем чистую или слегка подсоленную воду, поэтому приведенное выше объяснение справедливо. Но если мы поместим яйцо в действительно соленую среду (например, Мертвое море с соленостью около 342 ‰ ), как свежие, так и гнилые сорта будут плавать. Таким образом, с помощью этого метода невозможно решить, свежее яйцо или нет.Проверьте, каково критическое значение солености, при котором свежее яйцо может плавать, с помощью нашего калькулятора плотности воды!
Скорость звука в воде
Существует простая формула, описывающая скорость звука в воздухе: c . Его можно переписать как:
c = √ (γ * p / ρ) ,
, где γ — показатель адиабаты, p — давление, а ρ — плотность воздуха. Для большинства жидкостей соотношение обычно не так просто, но в целом скорость звука в воде повышается, когда плотность уменьшается в широком диапазоне температур .Знание зависимости скорости звука в соленой воде имеет решающее значение для всех исследований, связанных с измерениями сонара.
14.1 Жидкости, плотность и давление
Цели обучения
К концу этого раздела вы сможете:
- Назовите различные фазы материи
- Опишите характеристики фаз вещества на молекулярном или атомном уровне
- Различия между сжимаемыми и несжимаемыми материалами
- Определение плотности и связанных с ней единиц СИ
- Сравните и сопоставьте плотности различных веществ
- Определение давления и связанных с ним единиц СИ
- Объясните взаимосвязь между давлением и силой
- Рассчитать силу с учетом давления и площади
Материя чаще всего существует в твердом, жидком или газообразном состоянии; эти состояния известны как три общие фазы материи.В этом разделе мы подробно рассмотрим каждый из этих этапов.
Характеристики твердых тел
Твердые тела имеют определенные формы и объемы. Атомы или молекулы в твердом теле находятся в непосредственной близости друг от друга, и между этими молекулами существует значительная сила. Твердые тела будут принимать форму, определяемую природой этих сил между молекулами. Хотя настоящие твердые тела не являются несжимаемыми, тем не менее, для изменения формы твердого тела требуется большая сила.В некоторых случаях сила между молекулами может заставить молекулы организоваться в решетку, как показано на (Рисунок). Структура этой трехмерной решетки представлена в виде молекул, связанных жесткими связями (моделируемыми как жесткие пружины), которые обеспечивают ограниченную свободу движения. Даже большая сила вызывает только небольшие смещения в атомах или молекулах решетки, и твердое тело сохраняет свою форму. Твердые тела также сопротивляются силам сдвига. (Силы сдвига — это силы, прикладываемые по касательной к поверхности, как описано в разделе «Статическое равновесие и упругость».)
Характеристики жидкостей
Жидкости и газы считаются жидкостями , потому что они поддаются сдвиговым усилиям, тогда как твердые тела им сопротивляются. Подобно твердым телам, молекулы в жидкости связаны с соседними молекулами, но обладают гораздо меньшим количеством этих связей. Молекулы в жидкости не заблокированы на месте и могут двигаться относительно друг друга. Расстояние между молекулами аналогично расстояниям в твердом теле, поэтому жидкости имеют определенные объемы, но форма жидкости изменяется в зависимости от формы ее контейнера.Газы не связаны с соседними атомами и могут иметь большие расстояния между молекулами. У газов нет ни определенной формы, ни определенного объема, поскольку их молекулы движутся, чтобы заполнить емкость, в которой они содержатся ((Рисунок)).
Рис. 14.2 (a) Атомы в твердом теле всегда находятся в тесном контакте с соседними атомами, удерживаясь на месте силами, представленными здесь пружинами. (б) Атомы в жидкости также находятся в тесном контакте, но могут скользить друг по другу. Силы между атомами сильно сопротивляются попыткам сжать атомы.(c) Атомы в газе перемещаются свободно и разделены большими расстояниями. Газ должен храниться в закрытом контейнере, чтобы предотвратить его свободное расширение и утечку.
Жидкости легко деформируются при напряжении и не возвращаются к своей первоначальной форме после снятия силы. Это происходит потому, что атомы или молекулы в жидкости могут свободно перемещаться и менять соседей. То есть текут жидкости (так что они представляют собой тип жидкости), а молекулы удерживаются вместе за счет взаимного притяжения. Когда жидкость помещается в емкость без крышки, она остается в емкости.Поскольку атомы плотно упакованы, жидкости, как и твердые тела, сопротивляются сжатию; для изменения объема жидкости необходимо чрезвычайно большое усилие.
Напротив, атомы в газах разделены большими расстояниями, и поэтому силы между атомами в газе очень слабые, за исключением случаев, когда атомы сталкиваются друг с другом. Это позволяет относительно легко сжимать газы и позволяет им течь (что делает их жидкими). При помещении в открытый контейнер газы, в отличие от жидкостей, улетучиваются.
В этой главе мы обычно называем газы и жидкости просто жидкостями, проводя различие между ними только тогда, когда они ведут себя по-разному. Существует еще одна фаза вещества, плазма, которая существует при очень высоких температурах. При высоких температурах молекулы могут диссоциировать на атомы, а атомы диссоциировать на электроны (с отрицательными зарядами) и протоны (с положительными зарядами), образуя плазму. Плазма не будет подробно обсуждаться в этой главе, потому что плазма имеет очень разные свойства от трех других общих фаз материи, обсуждаемых в этой главе, из-за сильных электрических сил между зарядами.
Плотность
Предположим, что кусок латуни и кусок дерева имеют одинаковую массу. Если оба блока упали в резервуар с водой, почему дерево всплывает, а латунь тонет ((Рисунок))? Это происходит потому, что латунь имеет большую плотность, чем вода, тогда как древесина имеет меньшую плотность, чем вода.
Рис. 14.3 (a) Медный и деревянный брусок имеют одинаковый вес и массу, но деревянный брусок имеет гораздо больший объем. (b) При помещении в аквариум, наполненный водой, латунный куб тонет, а деревянный брусок плавает.(Деревянный брусок на обеих фотографиях одинаковый; он был повернут набок, чтобы поместиться на шкале.)
Плотность — важная характеристика веществ. Это очень важно, например, для определения того, тонет объект или плавает в жидкости.
Плотность
Средняя плотность вещества или объекта определяется как его масса на единицу объема,
[латекс] \ rho = \ frac {m} {V} [/ латекс]
, где греческая буква [латекс] \ rho [/ latex] (rho) обозначает плотность, м — масса, а V — объем.{3} [/ латекс]
Как вы можете видеть, исследуя (рисунок), плотность объекта может помочь определить его состав. Плотность золота, например, примерно в 2,5 раза больше плотности железа, что примерно в 2,5 раза больше плотности алюминия. Плотность также кое-что говорит о фазе материи и ее субструктуре. Обратите внимание, что плотности жидкостей и твердых тел примерно сопоставимы, что согласуется с тем фактом, что их атомы находятся в тесном контакте.Плотность газов намного меньше, чем у жидкостей и твердых тел, потому что атомы в газах разделены большим количеством пустого пространства. Газы отображаются для стандартной температуры [латекс] 0,0 \ text {°} \ text {C} [/ latex] и стандартного давления 101,3 кПа, при этом плотность сильно зависит от температуры и давления. Отображаемые плотности твердых и жидких тел даны для стандартной температуры [латекс] 0,0 \ text {°} \ text {C} [/ latex], а плотности твердых и жидких веществ зависят от температуры.Плотность твердых тел и жидкостей обычно увеличивается с понижением температуры.
(рисунок) показывает плотность воды в различных фазах и температуре. Плотность воды увеличивается с понижением температуры, достигая максимума при [латексе] 4.0 \ text {°} \ text {C,} [/ latex], а затем уменьшается, когда температура опускается ниже [латекс] 4. {3}) [/ латекс]
Плотность вещества не обязательно постоянна во всем объеме вещества. Если плотность во всем веществе постоянна, это вещество называется гомогенным веществом . Твердый железный пруток — это пример однородного вещества. Плотность постоянна повсюду, и плотность любого образца вещества равна его средней плотности. Если плотность вещества непостоянна, вещество считается гетерогенным веществом .Кусок швейцарского сыра является примером неоднородного материала, содержащего как твердый сыр, так и заполненные газом пустоты. Плотность в определенном месте внутри неоднородного материала называется локальной плотностью и задается как функция местоположения, [латекс] \ rho = \ rho (x, y, z) [/ latex] ((Рисунок)) .
Рис. 14.4 Плотность может варьироваться в неоднородной смеси. Локальная плотность в точке получается делением массы на объем в небольшом объеме вокруг данной точки.
Локальная плотность может быть получена с помощью процесса ограничения, основанного на средней плотности в небольшом объеме вокруг рассматриваемой точки, принимая предел, при котором размер объема приближается к нулю,
[латекс] \ rho = \ underset {\ text {Δ} V \ to 0} {\ text {lim}} \ frac {\ text {Δ} m} {\ text {Δ} V} [/ latex]
, где [латекс] \ rho [/ latex] — плотность, м, — масса, а V — объем.
Поскольку газы могут свободно расширяться и сжиматься, плотности газов значительно изменяются с температурой, тогда как плотности жидкостей мало меняются с температурой.Поэтому плотности жидкостей часто считаются постоянными, при этом плотность равна средней плотности.
Плотность — это размерная характеристика; поэтому при сравнении плотностей двух веществ необходимо учитывать единицы измерения. По этой причине для сравнения плотностей часто используется более удобная безразмерная величина, называемая удельным весом. Удельный вес определяется как отношение плотности материала к плотности воды в [латексе] 4.{3} [/ latex]), но его удельный вес составляет 2,7 независимо от единицы плотности. Удельный вес является особенно полезной величиной с точки зрения плавучести, которую мы обсудим позже в этой главе.
Давление
Вы, несомненно, слышали слово «давление», используемое по отношению к крови (высокое или низкое кровяное давление) и к погоде (погодные системы с высоким и низким давлением). Это только два из многих примеров давления в жидкости. (Напомним, что мы ввели идею давления в статическое равновесие и упругость в контексте объемных напряжений и деформаций.)
Давление
Давление ( p ) определяется как нормальная сила F на единицу площади A , к которой прилагается сила, или
[латекс] p = \ frac {F} {A}. [/ латекс]
Чтобы определить давление в определенной точке, давление определяется как сила dF , прилагаемая жидкостью к бесконечно малому элементу площади dA , содержащему точку, в результате чего [латекс] p = \ frac {dF} { dA} [/ латекс].
Данная сила может иметь существенно разный эффект в зависимости от области, на которую действует сила.{2}. [/ latex] Вот почему острая игла способна протыкать кожу при приложении небольшой силы, но приложение той же силы пальцем не протыкает кожу ((Рисунок)).
Рис. 14.5 (a) Человек, которого тыкают пальцем, может раздражать, но сила не имеет длительного эффекта. (b) Напротив, той же силы, приложенной к области размером с острый конец иглы, достаточно, чтобы сломать кожу.
Обратите внимание, что хотя сила — это вектор, давление — это скаляр.{2}. [/ латекс]
Для измерения давления используется несколько других единиц, которые мы обсудим позже в этой главе.
Изменение давления с глубиной в жидкости постоянной плотности
Давление определено для всех состояний вещества, но особенно важно при обсуждении жидкостей. Важной характеристикой жидкостей является отсутствие значительного сопротивления компоненту силы, приложенной параллельно поверхности жидкости. Молекулы жидкости просто текут, чтобы приспособиться к горизонтальной силе.Сила, приложенная перпендикулярно к поверхности, сжимает или расширяет жидкость. Если вы попытаетесь сжать жидкость, вы обнаружите, что сила реакции развивается в каждой точке внутри жидкости во внешнем направлении, уравновешивая силу, приложенную к молекулам на границе.
Рассмотрим жидкость постоянной плотности, как показано на (Рисунок). Давление в нижней части контейнера возникает из-за давления атмосферы [латекс] ({p} _ {0}) [/ латекс] плюс давление, обусловленное весом жидкости.Давление, создаваемое жидкостью, равно весу жидкости, деленному на площадь. Вес жидкости равен ее массе, умноженной на ускорение свободного падения.
Рисунок 14.6 Дно этого контейнера выдерживает весь вес находящейся в нем жидкости. Вертикальные стороны не могут оказывать восходящее усилие на жидкость (поскольку она не может выдерживать силу сдвига), поэтому дно должно поддерживать все это.
Поскольку плотность постоянна, вес можно рассчитать, используя плотность:
[латекс] w = mg = \ rho Vg = \ rho Ahg.[/ латекс]
Следовательно, давление на дне контейнера равно атмосферному давлению, добавленному к весу жидкости, разделенному на площадь:
[латекс] p = {p} _ {0} + \ frac {\ rho Ahg} {A} = {p} _ {0} + \ rho hg. [/ латекс]
Это уравнение применимо только для давления на глубине для жидкости постоянной плотности.
Давление на глубине для жидкости постоянной плотности
Давление на глубине в жидкости постоянной плотности равно давлению атмосферы плюс давление, обусловленное весом жидкости, или
[латекс] p = {p} _ {0} + \ rho hg, [/ latex]
Где p — давление на определенной глубине, [латекс] {p} _ {0} [/ latex] — давление атмосферы, [латекс] \ rho [/ latex] — плотность жидкости, g — ускорение свободного падения, а h — глубина.
Рис. 14.7 Плотина «Три ущелья», возведенная на реке Янцзы в центральном Китае в 2008 году, создала массивный водохранилище, в результате которого было перемещено более одного миллиона человек. (кредит: «Le Grand Portage» / Flickr)
Пример
Какую силу должна выдержать плотина?
Рассмотрим давление и силу, действующие на плотину, удерживающую резервуар с водой ((рисунок)). Предположим, что плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м, как показано ниже. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на дамбу.
Среднее давление p из-за веса воды — это давление на средней глубине h , равное 40,0 м, поскольку давление увеличивается линейно с глубиной. Сила, оказываемая водой на плотину, равна среднему давлению, умноженному на площадь контакта, [латекс] F = pA. [/ латекс]
раствор
- Среднее давление из-за веса жидкости составляет
[латекс] p = h \ rho g. [/ латекс]
Введите плотность воды из (Рисунок) и приняв h за среднюю глубину 40.{13} \ text {N} [/ latex] вес воды в резервуаре. На самом деле это всего 0,0800% от веса.
Проверьте свое понимание
Если водохранилище на (Рисунок) покрывает вдвое большую площадь, но сохраняется на той же глубине, потребуется ли перепроектировать плотину?
Показать решение
Давление, указанное в части (а) примера, полностью не зависит от ширины и длины озера; это зависит только от его средней глубины на плотине. Таким образом, сила зависит только от средней глубины воды и размеров плотины, а не от горизонтальной протяженности водохранилища.На диаграмме обратите внимание, что толщина дамбы увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличения давления.
Давление в статической жидкости в однородном гравитационном поле
Статическая жидкость — это жидкость, которая не движется. В любой точке статической жидкости давление со всех сторон должно быть одинаковым, иначе жидкость в этой точке отреагирует на результирующую силу и ускорится.
Давление в любой точке статической жидкости зависит только от глубины в этой точке.Как уже говорилось, давление в жидкости около Земли изменяется с глубиной из-за веса жидкости над определенным уровнем. В приведенных выше примерах мы предполагали, что плотность постоянна, а средняя плотность жидкости является хорошим представлением плотности. Это разумное приближение для жидкостей, таких как вода, где требуются большие силы для сжатия жидкости или изменения объема. В плавательном бассейне, например, плотность примерно постоянна, и вода внизу очень слабо сжимается под весом воды наверху.Однако путешествие в атмосфере — это совсем другая ситуация. Плотность воздуха начинает значительно меняться на небольшом расстоянии от поверхности Земли.
Чтобы вывести формулу для изменения давления с глубиной в резервуаре, содержащем жидкость плотностью ρ на поверхности Земли, мы должны исходить из предположения, что плотность жидкости непостоянна. Жидкость, расположенная на более глубоких уровнях, подвергается большей силе, чем жидкость, находящаяся ближе к поверхности, из-за веса жидкости над ней.Следовательно, давление, рассчитанное на данной глубине, отличается от давления, рассчитанного с использованием постоянной плотности.
Представьте себе тонкий элемент жидкости на глубине h , как показано на (Рисунок). Пусть элемент имеет площадь поперечного сечения A и высоту [латекс] \ text {Δ} y [/ latex]. Силы, действующие на элемент, возникают из-за давлений p ( y ) выше и [латекс] p (y + \ text {Δ} y) [/ latex] под ним. Вес самого элемента также показан на диаграмме свободного тела.
Рисунок 14.8 Силы, действующие на элемент массы внутри жидкости. Вес самого элемента показан на диаграмме свободного тела.
Поскольку элемент жидкости между y и [latex] y + \ text {Δ} y [/ latex] не ускоряется, силы уравновешены. Используя декартову ось y , ориентированную вверх, мы находим следующее уравнение для -компоненты y :
[латекс] p (y + \ text {Δ} y) A-p (y) A-g \ text {Δ} m = 0 (\ text {Δ} y> 0). [/ латекс]
Обратите внимание, что если бы элемент имел ненулевую составляющую ускорения y , правая часть не была бы равна нулю, а вместо этого была бы массой, умноженной на y -ускорение.Массу элемента можно записать через плотность жидкости и объем элементов:
[латекс] \ text {Δ} m = | \ rho A \ text {Δ} y | = \ text {-} \ rho A \ text {Δ} y \ text {} (\ text {Δ} y> 0 ). [/ латекс]
Помещая это выражение для [latex] \ text {Δ} m [/ latex] в (Рисунок), а затем разделив обе стороны на [latex] A \ text {Δ} y [/ latex], мы находим
[латекс] \ frac {p (y + \ text {Δ} y) -p (y)} {\ text {Δ} y} = \ text {-} \ rho g. [/ латекс]
Взяв предел бесконечно тонкого элемента [латекс] \ text {Δ} y \ до 0 [/ latex], мы получаем следующее дифференциальное уравнение, которое дает изменение давления в жидкости:
[латекс] \ frac {dp} {dy} = \ text {-} \ rho g.[/ латекс]
Это уравнение говорит нам, что скорость изменения давления в жидкости пропорциональна плотности жидкости. Решение этого уравнения зависит от того, является ли плотность ρ постоянной или изменяется с глубиной; то есть функция ρ ( y ).
Если диапазон анализируемой глубины не слишком велик, мы можем считать плотность постоянной. Но если диапазон глубин достаточно велик для того, чтобы плотность могла заметно меняться, как, например, в случае атмосферы, происходит значительное изменение плотности с глубиной.В этом случае мы не можем использовать приближение постоянной плотности.
Давление в жидкости постоянной плотности
Давайте воспользуемся (рис.), Чтобы составить формулу для давления на глубине h от поверхности в резервуаре с жидкостью, такой как вода, где плотность жидкости можно считать постоянной.
Нам нужно интегрировать (рисунок) из [latex] y = 0, [/ latex], где давление является атмосферным давлением [latex] ({p} _ {0}), [/ latex], в [latex] y = \ текст {-} h, [/ latex] y — координата глубины:
[латекс] \ begin {array} {ccc} \ hfill {\ int} _ {{p} _ {0}} ^ {p} dp & = \ hfill & \ text {-} {\ int} _ {0} ^ {\ text {-} h} \ rho gdy \ hfill \\ \ hfill p- {p} _ {0} & = \ hfill & \ rho gh \ hfill \\ \ hfill p & = \ hfill & {p} _ {0} + \ rho gh.\ hfill \ end {array} [/ latex]
Следовательно, давление на глубине жидкости на поверхности Земли равно атмосферному давлению плюс ρgh , если плотность жидкости постоянна по высоте, как мы обнаружили ранее.
Обратите внимание, что давление в жидкости зависит только от глубины от поверхности, а не от формы контейнера. Таким образом, в контейнере, где жидкость может свободно перемещаться в различных частях, жидкость остается на одном уровне во всех частях, независимо от формы, как показано на (Рисунок).
Рисунок 14.9 Если жидкость может свободно течь между частями контейнера, она поднимается на одинаковую высоту в каждой части. В изображенном контейнере давление внизу каждой колонки одинаковое; если бы это было не так, жидкость текла бы до тех пор, пока давления не сравнялись бы.
Изменение атмосферного давления с высотой
Особый интерес представляет изменение атмосферного давления с высотой. Предполагая, что температура воздуха постоянна и что закон термодинамики идеального газа описывает атмосферу в хорошем приближении, мы можем найти изменение атмосферного давления с высотой, когда температура постоянна.(Мы обсудим закон идеального газа в следующей главе, но мы предполагаем, что вы знакомы с ним из средней школы и химии.) Пусть p ( y ) будет атмосферным давлением на высоте y . Плотность [латекс] \ rho [/ latex] при y , температура T в шкале Кельвина (K) и масса m молекулы воздуха связаны с абсолютным давлением идеальным газом. закон, по форме
[латекс] p = \ rho \ frac {{k} _ {\ text {B}} T} {m} \, \ text {(атмосфера),} [/ латекс]
где [latex] {k} _ {\ text {B}} [/ latex] — постоянная Больцмана, значение которой равно [latex] 1.{-23} \ text {J / K} [/ латекс].
Вы, возможно, встречали закон идеального газа в форме [латекс] pV = nRT [/ latex], где n — число молей, а R — газовая постоянная. Здесь тот же закон был записан в другой форме, используя плотность [латекс] \ rho [/ latex] вместо объема V . Следовательно, если давление p изменяется с высотой, изменяется и плотность [латекс] \ rho. [/ latex] Используя плотность из закона идеального газа, скорость изменения давления с высотой определяется как
[латекс] \ frac {dp} {dy} = \ text {-} p (\ frac {mg} {{k} _ {\ text {B}} T}), [/ latex]
, где в скобках указаны постоянные количества.{y} \ hfill \\ \ hfill \ text {ln} (p) — \ text {ln} ({p} _ {0}) & = \ hfill & \ text {-} \ alpha y \ hfill \\ \ hfill \ text {ln} (\ frac {p} {{p} _ {0}}) & = \ hfill & \ text {-} \ alpha y \ hfill \ end {array} [/ latex]
Это дает решение
[латекс] p (y) = {p} _ {0} \ text {exp} (\ text {-} \ alpha y). [/ латекс]
Таким образом, атмосферное давление экспоненциально падает с высотой, поскольку ось y направлена вверх от земли, а y имеет положительные значения в атмосфере над уровнем моря.Давление падает в [латекс] \ frac {1} {e} [/ latex] при высоте [латекс] \ frac {1} {\ alpha}, [/ latex], что дает нам физическую интерпретацию для [latex] \ alpha [/ latex]: Константа [latex] \ frac {1} {\ alpha} [/ latex] представляет собой шкалу длины, которая характеризует изменение давления с высотой и часто называется высотой шкалы давления.
Мы можем получить приблизительное значение [латекс] \ альфа [/ латекс], используя массу молекулы азота в качестве заместителя для молекулы воздуха.{-23} \, \ text {J / K} \, × \, \ text {300 K}} = \ frac {1} {8800 \, \ text {m}}. [/ латекс]
Следовательно, на каждые 8800 метров давление воздуха падает в 1/ e , или примерно на одну треть своего значения. Это дает нам лишь приблизительную оценку реальной ситуации, поскольку мы предположили и постоянную температуру, и постоянную температуру g на таких больших расстояниях от Земли, что в действительности не является правильным.
Направление давления в жидкости
Давление жидкости не имеет направления, будучи скалярной величиной, тогда как силы, возникающие под давлением, имеют четко определенные направления: они всегда действуют перпендикулярно любой поверхности.Причина в том, что жидкости не могут противостоять усилиям сдвига или проявлять их. Таким образом, в статической жидкости, заключенной в резервуар, сила, действующая на стенки резервуара, действует перпендикулярно внутренней поверхности. Точно так же давление действует перпендикулярно к поверхностям любого объекта в жидкости. (Рисунок) иллюстрирует давление, оказываемое воздухом на стенки шины и водой на тело пловца.
Рисунок 14.10 (a) Давление внутри этой шины оказывает силы, перпендикулярные всем поверхностям, с которыми она контактирует.Стрелки показывают направления и величины сил, действующих в различных точках. (b) Давление оказывается перпендикулярно всем сторонам этого пловца, так как вода текла бы в пространство, которое он занимает, если бы его там не было. Стрелки показывают направления и величины сил, действующих на пловца в различных точках. Обратите внимание, что силы снизу больше из-за большей глубины, что дает чистую восходящую или выталкивающую силу. Чистая вертикальная сила, действующая на пловца, равна сумме выталкивающей силы и веса пловца.
Какова плотность воды? По температуре и единицам измерения
Какая плотность воды? Имеет значение, какая температура? Как определить плотность других предметов и жидкостей?
В этом руководстве мы объясняем плотность воды, предоставляем диаграмму, которую вы можете использовать для определения плотности воды при различных температурах, и объясняем три различных способа вычисления плотности.
Какова плотность воды?
Плотность — это масса единицы объема вещества. Плотность воды чаще всего дается как 1 г / см. 3 , , но ниже представлена плотность воды в различных единицах измерения.
Установка Плотность воды Плотность воды г / см 3 1 г / см 3 Плотность воды г / мл 1 г / мл Плотность воды кг / м 3 1000 кг / м 3 Плотность воды фунт / фут 3 62.4 фунта / фут 3 Не случайно вода имеет плотность 1. Плотность — это масса, деленная на объем (ρ = m / v), и вода использовалась в качестве основы для установления метрической единицы массы, что означает кубический сантиметр (1 см 3 ) воды весит один грамм (1 г).
Итак, 1 г / 1 см 3 = 1 г / см 3 , что придает воде легко запоминающуюся плотность. Однако точная плотность воды зависит как от давления воздуха, так и от температуры в помещении. Эти изменения плотности очень незначительны, поэтому, если вам не нужны очень точные вычисления или если эксперимент проводится в области с экстремальной температурой / давлением, вы можете продолжать использовать 1 г / см 3 для плотности воды. Вы можете посмотреть на диаграмму в следующем разделе, чтобы увидеть, как плотность воды изменяется с температурой.
Обратите внимание, что эти значения плотности воды действительны только для чистой воды. Морская вода (как и океаны) имеет разную плотность, которая зависит от того, сколько соли растворено в воде.Плотность морской воды обычно немного выше плотности чистой воды, примерно 1,02 г / см 3 до 1,03 г / см 3 .
Плотность воды при разных температурах
Ниже приведена диаграмма, которая показывает плотность воды (в граммах / см 3 ) при различных температурах, от точки ниже точки замерзания (-22 ° F / -30 ° C) до ее точка кипения (212 ° F / 100 ° C).
Как вы можете видеть на диаграмме, вода имеет точную плотность только 1 г / см 3 при 39.2 ° F или 4,0 ° C. Как только вы опускаетесь ниже точки замерзания воды (32 ° F / 0 ° C), плотность воды уменьшается, потому что лед менее плотен, чем вода. Вот почему лед плавает над водой, и когда вы кладете кубики льда в стакан с водой, они не просто опускаются на дно.
Диаграмма также показывает, что для диапазона температур, типичных для внутренних научных лабораторий (от 50 ° F / 10 ° C до 70 ° F / 21 ° C), плотность воды очень близка к 1 г / см. 3 , поэтому это значение используется во всех расчетах плотности, кроме самых точных.Только когда температура станет очень экстремальной в том или ином направлении (близкой к температуре замерзания или кипения), температура воды изменится настолько, что 1 г / см 3 больше не будет приемлемо точным.
Температура (° F / ° C) Плотность воды (граммы / см 3 ) -22 ° / -30 ° 0,98385 -4 ° / -20 ° 0,99355 14 ° / -10 ° 0.99817 32 ° / 0 ° 0,99987 39,2 ° / 4,0 ° 1,00000 40 ° / 4,4 ° 0,99999 50 ° / 10 ° 0,99975 60 ° / 15,6 ° 0,99907 70 ° / 21 ° 0,99802 80 ° / 26,7 ° 0,99669 90 ° / 32,2 ° 0,99510 100 ° / 37.8 ° 0.99318 120 ° / 48,9 ° 0,98870 140 ° / 60 ° 0,98338 160 ° / 71,1 ° 0,97729 180 ° / 82,2 ° 0,97056 200 ° / 93,3 ° 0,96333 212 ° / 100 ° 0,95865 Источник: USGS
Как рассчитать плотность вещества
Итак, знайте, что вы знаете, какова плотность воды при разных температурах, но что, если вы хотите найти плотность чего-то, что не является водой? На самом деле это довольно просто!
Плотность любого вещества можно найти, разделив его массу на его объем.Формула плотности: ρ = m / v , где плотность обозначается символом ρ (произносится как «ро»).
Существует три основных способа вычисления плотности, в зависимости от того, пытаетесь ли вы определить плотность объекта правильной формы, объекта неправильной формы или жидкости, и если у вас есть какие-либо специальные инструменты, такие как ареометр.
Расчет плотности обычного объекта
Для обычных объектов (тех, чьи грани являются стандартными многоугольниками, такими как квадраты, прямоугольники, треугольники и т. Д.) вы можете довольно легко вычислить массу и объем. Масса объекта — это просто его вес, и у всех правильных многоугольников есть уравнение для определения их объема на основе их длины, ширины и высоты.
Например, у вас есть прямоугольный кусок алюминия весом 865 г и размерами 10 x 8 x 4 см. Сначала вы должны найти объем куска алюминия, умножив длину, ширину и высоту (что является уравнением для объема прямоугольника).
V = 10 см x 8 см x 4 см = 320 см 3
Затем вы разделите массу на объем, чтобы получить плотность (ρ = m / v).
865 г / 320 см 3 = 2,7 г / см 3
Таким образом, плотность алюминия составляет 2,7 г / см. 3 , и это верно для любого куска (чистого и твердого) алюминия, независимо от его размера.
Расчет плотности жидкости или объекта неправильной формы
Если объект имеет неправильную форму и вы не можете легко вычислить его объем, вы можете определить его объем, поместив его в градуированный цилиндр, наполненный водой, и измерив объем воды, который он вытесняет. Принцип Архимеда гласит, что объект вытесняет объем жидкости, равный его собственному объему. Как только вы найдете объем, вы должны использовать стандартное уравнение ρ = m / v.
Итак, если бы у вас был другой кусок алюминия неправильной формы, который весил 550 г и вытеснил 204 мл воды в градуированном цилиндре, тогда ваше уравнение было бы ρ = 550 г / 204 мл = 2,7 г / мл.
Если вещество, плотность которого вы пытаетесь определить, является жидкостью, вы можете просто налить жидкость в мерный цилиндр и посмотреть, каков его объем, а затем вычислить оттуда плотность.
Расчет плотности жидкости с помощью ареометра
Если вы пытаетесь рассчитать плотность жидкости, вы также можете сделать это с помощью прибора, известного как ареометр. Ареометр выглядит как термометр с большой грушей на одном конце, чтобы он плавал.
Чтобы использовать его, просто осторожно опустите ареометр в жидкость, пока ареометр не начнет плавать самостоятельно. Найдите, какая часть ареометра находится прямо у поверхности жидкости, и прочтите число на боковой стороне ареометра.Это будет плотность. Ареометры плавают ниже в менее плотных жидкостях и выше в более плотных жидкостях.
Резюме: Какова плотность воды?
Плотность воды обычно округляется до 1 г / см 3 или 1000 кг / м 3 , , если вы не выполняете очень точные вычисления или не проводите эксперимент при экстремальных температурах. Плотность воды меняется в зависимости от температуры, поэтому, если вы проводите эксперимент, близкий к точке кипения или замерзания воды или превышающей ее, вам нужно будет использовать другое значение, чтобы учесть изменение плотности.И пар, и лед менее плотны, чем вода.
Уравнение плотности: ρ = m / v.
Чтобы измерить плотность вещества, вы можете рассчитать объем объекта правильной формы и, исходя из этого, измерить объем жидкости или то, сколько жидкости неправильный объект вытесняет в градуированном цилиндре, или использовать ареометр для измерения плотность жидкости.
Что дальше?
Теперь, когда вы знаете, почему плотность воды уникальна, но как насчет других ее характеристик? Узнайте, почему у воды особенная теплоемкость.
Ищете другие темы, связанные с физикой? Мы научим вас вычислять ускорение с помощью этих трех основных формул и дадим вам два простых примера закона сохранения массы.
Хотите узнать о самых быстрых и простых способах конвертации между градусами Фаренгейта и Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот).
Вы изучаете облака в своем классе естественных наук? Получите помощь в определении различных типов облаков с помощью нашего экспертного руководства.
Пишете исследовательскую работу для школы, но не знаете, о чем писать? В нашем справочнике по темам исследовательских работ более 100 тем в десяти категориях, так что вы можете быть уверены, что найдете идеальную тему для себя.
Плотность воды — влияние давления и температуры
Свойства воды
Вода представляет собой прозрачное вещество без вкуса и запаха, которое может находиться в трех состояниях: жидком (вода), твердом (лед) и газообразном (пар). ). Одна молекула воды (h3O) состоит из двух атомов водорода и одного атома кислорода, связанных двумя ковалентными связями.Плотность воды, то есть масса на единицу объема воды, имеет некоторые интересные особенности, отличные от других жидкостей. В отличие от обычных жидкостей, плотность воды снижается с 40C до 00C. Выше 40 ° C плотность воды уменьшается с повышением температуры. Такое поведение называется «аномалией плотности». Благодаря этому свойству плотность льда меньше плотности воды при 40C (максимальная плотность).
Что такое плотность?
Плотность вещества определяется как масса, присутствующая в единице объема этого вещества.Еще одно полезное понятие — это числовая плотность, которая в основном используется при изучении теории газа. Он выражается количеством молекул, присутствующих в единице объема. Плотность — это внутреннее свойство вещества, имеющего единицы измерения кг / м3 в СИ и г / см3 в методах СГС.
Плотность воды при комнатной температуре
Плотность воды определяется аналогично другим веществам. При комнатной температуре (~ 200С) его значение составляет 998,2 кг / м3. Плотность воды при 25 градусах Цельсия составляет 997 кг / м3. При комнатной температуре вода остается в жидком состоянии.Плотность дистиллированной воды такая же. Морская вода содержит соли и минералы, поэтому ее плотность выше, чем у обычной воды. У поверхности моря плотность около 1027 кг / м3.
Влияние давления на плотность
Плотность увеличивается при повышении давления и уменьшается при понижении давления. По мере увеличения давления молекулы вещества сближаются, что приводит к увеличению плотности. С другой стороны, когда давление уменьшается, молекулы отдаляются. За счет этого снижается плотность.То же самое происходит и с водой.
Влияние температуры на плотность жидкости
Обычно жидкость расширяется при повышении температуры. В результате его плотность уменьшается. Расширение единицы объема жидкости при увеличении температуры на единицу определяется как коэффициент расширения (\ [\ gamma \]) жидкости. Если объем и плотность при температуре \ [T_ {1} \] равны \ [V_ {1} \] и \ [\ rho_ {1} \] соответственно, объем \ [V_ {2} \] и плотность \ [ \ rho_ {2} \] при температуре \ [T_ {2} \] можно получить как,
\ [V_ {2} \] = \ [V_ {1} \] [1 + \ [\ gamma \] (\ [T_ {2} \] — \ [T_ {1} \])]
\ [\ rho_ {2} \] = \ [\ rho_ {1} \] [1 — \ [\ gamma \] (\ [T_ {2} \] — \ [T_ {1} \])]
Для большинства жидкостей положительно i.е. плотность увеличивается с понижением температуры. Но вода ведет себя иначе.
Аномальное расширение воды
Плотность воды увеличивается от 00C до 40C, в отличие от обычных жидкостей. Плотность воды максимальна при 40C, а объем достигает минимума. Выше этой температуры вода ведет себя как обычная жидкость, т.е. ее плотность уменьшается. Максимальная плотность воды 1000 кг / м3. Графики плотности и объема с температурой показаны ниже:
(Изображение будет добавлено в ближайшее время)
Графики объема и плотности
Это поведение также называется аномалией плотности.
Плотность чистой воды для температур в диапазоне от 00 до 1000 ° C приведена ниже:
Плотность воды при разных температурах
Температура в 0 ° C
Плотность воды в кг / м3
Плотность воды в г / см3
Поведение
Коэффициент расширения
0
999.87
0,99987
Аномальное
(увеличение плотности)
Отрицательное
1
999.98
9018
9018
9018
9018 999,97
0,99997
3
999,99
0,99999
4
1
64 0 1
1
64 000000
Наивысшая плотность воды
Стационарная
5
999,99
0,99999
9182 9182 9182 9182 9183
8
999,88
0,99988
10
999.73
0,99973
20
998,23
0,99823
30
99861
8
64
6
8
8
992,24
0,99224
50
988,07
0,98807
60
6424
0,98324
70
977,81
0,97781
80
4
64
80
4
64
80
43
64
80
43
64
965.34
0,96534
100
958,38
0,95838
ens высокая температура снижает тепловую энергию молекул воды.Молекулы сближаются, и плотность увеличивается.
Поведение при температуре ниже 40 ° C: в этом температурном диапазоне, когда молекулы воды приближаются, они становятся способными образовывать стабильные водородные связи. Из-за отсутствия теплового движения образуется все больше и больше водородных связей. Это предотвращает сближение молекул и снижает плотность.
Поведение при 40 ° C: около этой температуры тепловое перемешивание и образование водородных связей имеют тенденцию уравновешивать друг друга, давая стационарное поведение плотности.Итак, плотность воды при 4 градусах Цельсия максимальная, а удельный объем минимальный.
Плавучие айсберги: Плотность льда составляет одну девятую плотности воды из-за аномалии плотности воды. Итак, айсберги плавают в океанах, причем 90% их объема находится под водой.
Влияние на морскую жизнь: В холодных регионах температура атмосферы постепенно понижается до 00C и ниже.Вода на поверхности озер и океанов остывает и становится тяжелой. Холодная вода идет внизу, а горячая поднимается. Этот процесс конвекции продолжается до тех пор, пока температура воды на нижних поверхностях не станет около 40 ° C. Поскольку это значение плотности воды максимальное, вода с верхних поверхностей больше не может стекать, и процесс конвекции прекращается. Верхние слои еще больше остывают и превращаются в лед. Затем лед плавает на поверхности воды. Однако нижние слои остаются при 40 ° C, что достаточно для выживания водных животных.
Плотность воды при 40 ° C максимальна, и при этой температуре она находится в жидком состоянии. Лед имеет меньшую плотность, чем вода.
Айсберги плавают на воде, но 90% объема айсберга остается под водой. Это стало причиной гибели Титаника.
«Конкуренция» между образованием водородных связей и тепловым движением молекул воды является причиной максимальной плотности воды при 40 ° C.
График зависимости плотности от температуры плоский около 40 ° C, т.е. плотность не меняется. Плотность воды при 40 ° C используется для определения единицы плотности. Он также использовался для определения единицы массы.
Некоторые обычно используемые коэффициенты объемного расширения включают воду: 0,0002 (м 3 / м 3 o C) и этиловый спирт: 0,0011 (м 3 / м 3 o C).
Для газовой постоянной сухого воздуха используйте: 287,05 Дж / (кг * град К).
Вам необходимо знать давление газа, измеренное в паскалях. Если у вас есть только давление в мбар, умножьте давление в мб на 100, чтобы преобразовать давление газа в паскалях.
- Взвесьте мерный цилиндр или химический стакан.
- Залейте жидкость и запишите результат измерения объема.
- Взвесьте стеклянную посуду с жидкостью.
- Найдите массу жидкости. Возьмите массу жидкости плюс стакан и вычтите вес стакана.
- Найдите плотность, разделив массу жидкости на объем. Обязательно записывайте единицы массы и объема.
(Изображение будет добавлено в ближайшее время)
Водородные связи в воде и льду
Примеры
(Изображение будет добавлено в ближайшее время)
Акватории в холодных регионах
Знаете ли вы?
Как рассчитать плотности при различных температурах
Обновлено 14 декабря 2020 г.
Афина Хессонг
Чтобы узнать, как температура влияет на плотность жидкого вещества, используйте один из двух методов в зависимости от жидкости, которую вы хотите измерить .Для газов используйте адаптацию закона идеального газа, который при переписывании дает уравнение для плотности на основе температуры и давления. Для других жидкостей, таких как вода или спирт, вы должны использовать дополнительную информацию, чтобы определить их плотность при различных температурах. Когда у вас есть вся информация, необходимая для расчета, его решение требует небольшой математики.
Найдите плотность жидкостей
Вычтите конечную температуру в градусах Цельсия из начальной температуры в градусах Цельсия.o \ text {C}
Умножьте эту разницу температур на коэффициент объемного температурного расширения измеряемого вещества, затем прибавьте к этому числу единицу. Для воды используйте ее коэффициент объемного температурного расширения (0,0002 м 3 / м 3 градусов C) и умножьте его на разницу температур, которая в этом примере составляет 10 градусов C. Выполните:
0,0002 \ times 10 = 0,002
Добавьте единицу к этому числу, чтобы получить: 1 + 0,002 = 1,002.
Разделите начальную плотность жидкости на это число, чтобы найти конечную плотность при новой температуре.3
Найдите плотность газов
Добавьте 273,15 к градусам Цельсия, чтобы найти градусы в Кельвинах. Например, температура 10 градусов Цельсия:
T = 10 + 273,15 = 283,15 \ text {Kelvin}
Умножьте температуру в Кельвинах на газовую постоянную. В сухом воздухе с газовой постоянной 287,05 Дж рассчитайте:
283,15 \ times 287,05 = 81278,21
Разделите это число на текущее давление, измеренное в паскалях, чтобы найти плотность в кг / м3.3.
Какова плотность воды?
Плотность воды зависит от температуры и чистоты. (авторское право: Anne Helmenstine)
Плотность воды — это масса воды на единицу объема. Практически это то же самое, что и вес воды на единицу объема. Плотность воды составляет около 1 грамм на миллилитр (г / мл), 1 грамм на кубический сантиметр (г / см 3 ), 1000 кг / м 3 или 62 фунта на кубический фут (фунт / фут 3). ).Точное значение на самом деле немного ниже и зависит от температуры. Максимальная плотность воды составляет 0,9998395 г / мл при 4,0 ° C (39,2 ° F).
Влияние температуры на плотность чистой воды
Иногда округление значения плотности воды до 1 г / мл недостаточно. К счастью, существуют таблицы значений плотности для разных температур:
| Температура (° F / ° C) | Плотность (граммы / см 3 | Вес (фунты / футы 3 | ||||
|---|---|---|---|---|---|---|
| 0 ° C / 32 ° F | 0.99987 | 62,416 | ||||
| 39,2 ° F / 4,0 ° C | 1,00000 | 62,424 | ||||
| 40 ° F / 4,4 ° C | 0,99999 | 62,423 | 0,99975 | 62,408 | ||
| 15,6 ° C / 60 ° F | 0,99907 | 62,366 | ||||
| 70 ° F / 21 ° C | 0,99802 | 0,99802 | 62,300 | |||
| 0,99669 | 62,217 | |||||
| 90 ° F / 32.2 ° C | 0,99510 | 62,118 | ||||
| 100 ° F / 37,8 ° C | 0,99318 | 61,998 | ||||
| 120 ° F / 48,9 ° C | 0,98861 14014 | 0,98870 | / 60 ° C | 0,98338 | 61,386 | |
| 160 ° F / 71,1 ° C | 0,97729 | 61,006 | ||||
| 180 ° F / 82,2 ° C | 0,97061 60814 | 0.96333 | 60,135 | |||
| 212 ° F / 100 ° C | 0,95865 | 59,843 |
Плотность чистой воды при различных температурах.
Другие факторы, влияющие на плотность воды
Помимо температуры на плотность воды влияют и другие факторы. Давление влияет на плотность, но, поскольку вода не очень сжимаема, обычно это не имеет большого значения. Плотность также зависит от того, сколько растворенного вещества находится в воде. Растворенные газы могут сделать воду менее плотной.Растворенные соли, минералы и другие химические вещества могут сделать воду более плотной. Например, морская вода более плотная, чем чистая вода.
Как определить плотность жидкости
Самый простой способ измерить плотность жидкости, включая воду, — это использовать ареометр. Типичный ареометр состоит из утяжеленной колбы с цилиндрическим стержнем. Линии, нанесенные на стержень, показывают, насколько глубоко луковица погружается в жидкость. Чем ниже опускается луковица, тем меньше плотность; чем выше плавает колба, тем выше плотность жидкости.Калибровка линий осуществляется путем погружения ареометра в жидкость с известной плотностью. Обычно стандартом является вода, потому что ее удельный вес составляет 1.000 при температуре около 4 ° C.
Измерение массы и объема — еще один способ определения плотности жидкости.
Лед менее плотен, чем вода
Обычно твердая форма соединения тяжелее или плотнее, чем его жидкость. С водой дело обстоит иначе. Лед примерно на 9% менее плотный, чем вода. Кубики льда плавают в стакане воды, а айсберги плавают в море. Причина, по которой вода более плотная, чем лед, связана с водородными связями. Притяжение между положительно заряженными атомами водорода молекулы воды к отрицательно заряженным атомам кислорода соседних молекул воды притягивает частицы жидкости очень близко друг к другу.Жесткая кристаллическая структура твердой воды (льда) удерживает молекулы немного дальше друг от друга.
Это свойство имеет значение для жизни. Если бы лед был тяжелее воды, он опустился бы на дно рек и озер, и они замерзли бы снизу вверх. Поскольку вода является отличным теплоизолятором, глубокие озера летом могут никогда не таять, и экосистема будет совсем другой.
Тяжелый водный лед плавает или тонет?
Тяжелый лед тонет в воде, поскольку имеет большую плотность.(фото: Майк Уокер)
В тяжелой воде обычные атомы водорода заменены атомами дейтерия. Обычный водород — это изотоп протий, в котором атомы имеют один протон и один электрон. Дейтерий — это изотоп водорода, в котором атомы имеют один протон, один нейтрон и один электрон. В формуле для тяжелой воды написано D 2 O, чтобы отразить разницу. Добавление нейтрона к каждому атому водорода делает дейтерий на 10,6% более плотным, чем обычная вода. Лед из тяжелой воды плавает в тяжелой воде, но тонет в обычной воде.

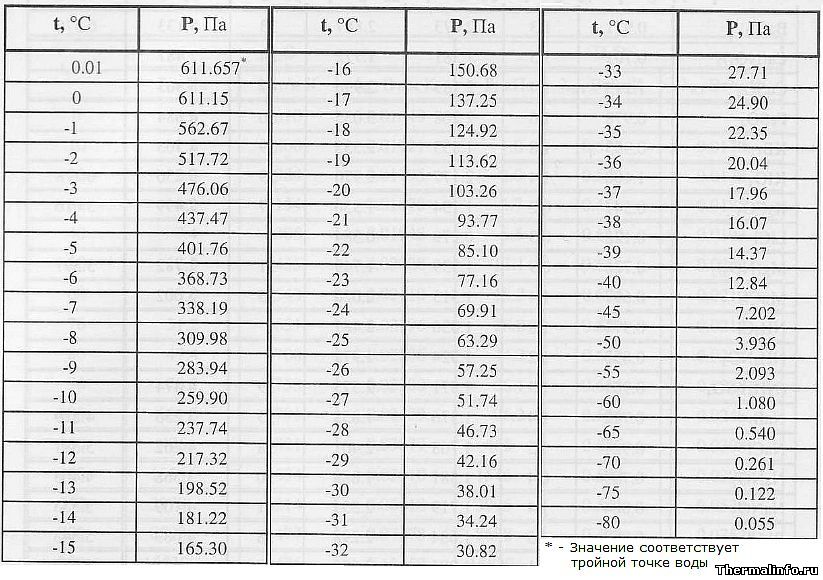 01
01 001000
001000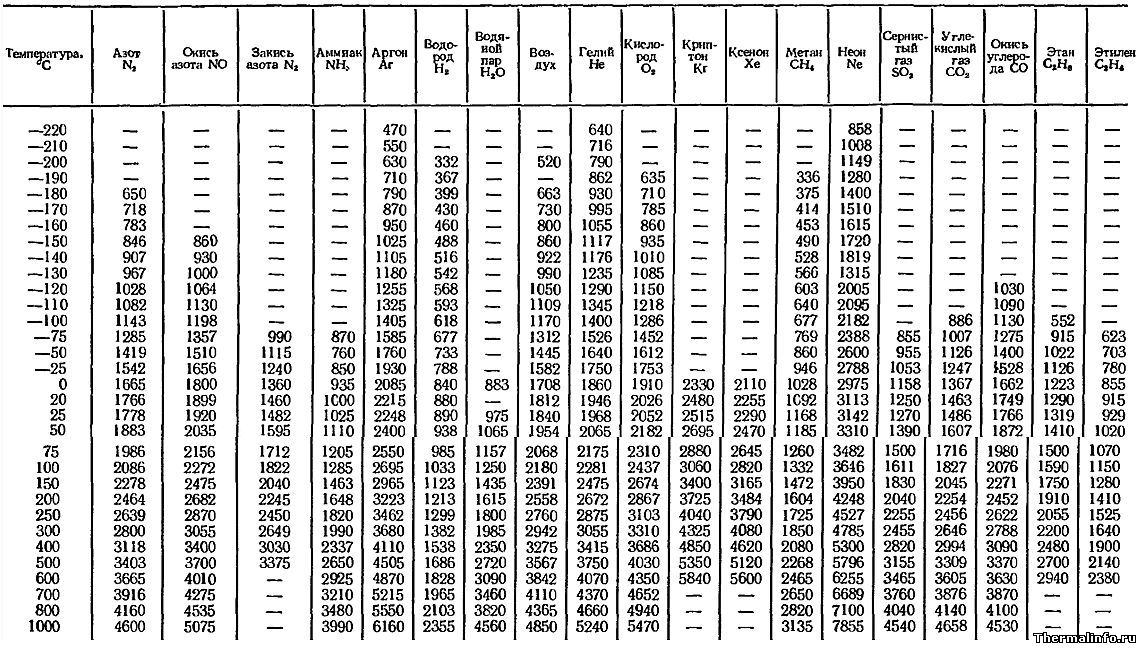 307
307